PottsMGNet: A Mathematical Explanation of Encoder-Decoder Based Neural Networks

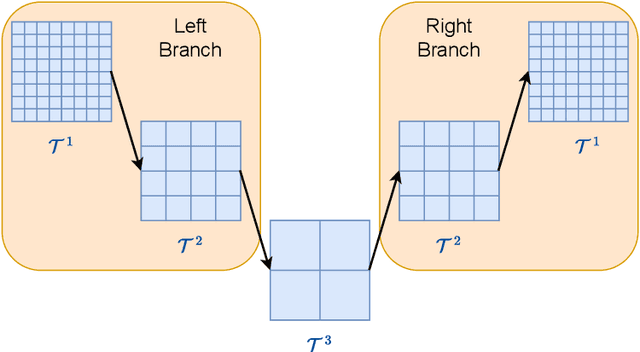
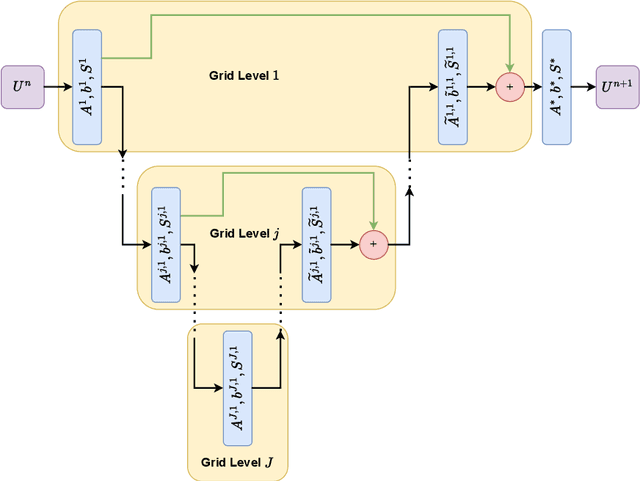
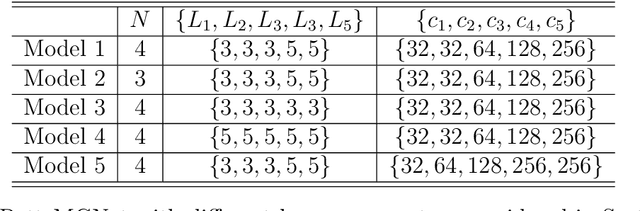
For problems in image processing and many other fields, a large class of effective neural networks has encoder-decoder-based architectures. Although these networks have made impressive performances, mathematical explanations of their architectures are still underdeveloped. In this paper, we study the encoder-decoder-based network architecture from the algorithmic perspective and provide a mathematical explanation. We use the two-phase Potts model for image segmentation as an example for our explanations. We associate the segmentation problem with a control problem in the continuous setting. Then, multigrid method and operator splitting scheme, the PottsMGNet, are used to discretize the continuous control model. We show that the resulting discrete PottsMGNet is equivalent to an encoder-decoder-based network. With minor modifications, it is shown that a number of the popular encoder-decoder-based neural networks are just instances of the proposed PottsMGNet. By incorporating the Soft-Threshold-Dynamics into the PottsMGNet as a regularizer, the PottsMGNet has shown to be robust with the network parameters such as network width and depth and achieved remarkable performance on datasets with very large noise. In nearly all our experiments, the new network always performs better or as good on accuracy and dice score than existing networks for image segmentation.