Multiple Convex Objects Image Segmentation via Proximal Alternating Direction Method of Multipliers

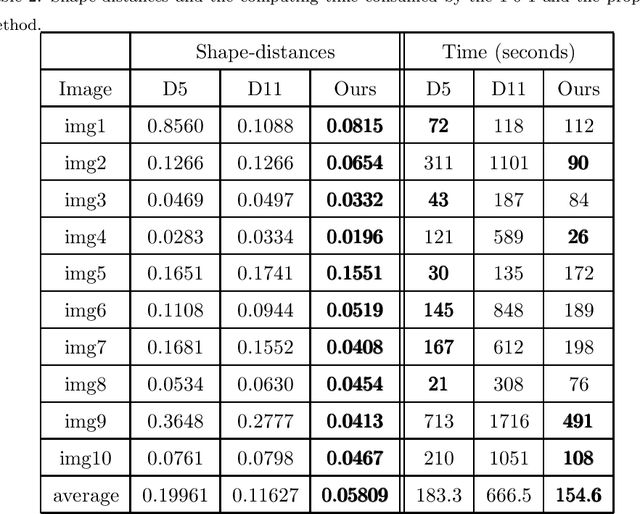
This paper focuses on the issue of image segmentation with convex shape prior. Firstly, we use binary function to represent convex object(s). The convex shape prior turns out to be a simple quadratic inequality constraint on the binary indicator function associated with each object. An image segmentation model incorporating convex shape prior into a probability-based method is proposed. Secondly, a new algorithm is designed to solve involved optimization problem, which is a challenging task because of the quadratic inequality constraint. To tackle this difficulty, we relax and linearize the quadratic inequality constraint to reduce it to solve a sequence of convex minimization problems. For each convex problem, an efficient proximal alternating direction method of multipliers is developed to solve it. The convergence of the algorithm follows some existing results in the optimization literature. Moreover, an interactive procedure is introduced to improve the accuracy of segmentation gradually. Numerical experiments on natural and medical images demonstrate that the proposed method is superior to some existing methods in terms of segmentation accuracy and computational time.