Roland Glowinski
Elastica Models for Color Image Regularization
Mar 18, 2022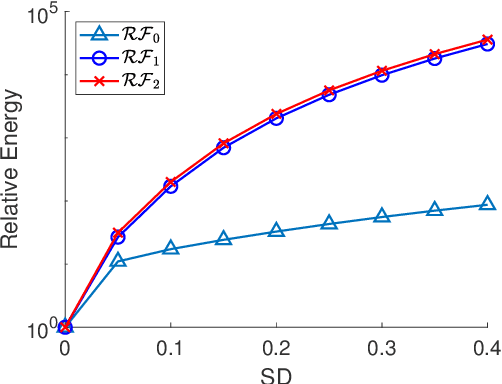

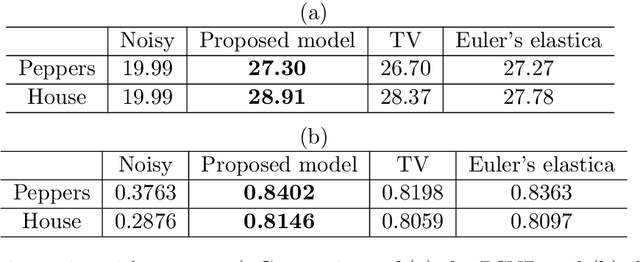
Abstract:One classical approach to regularize color is to tream them as two dimensional surfaces embedded in a five dimensional spatial-chromatic space. In this case, a natural regularization term arises as the image surface area. Choosing the chromatic coordinates as dominating over the spatial ones, the image spatial coordinates could be thought of as a paramterization of the image surface manifold in a three dimensional color space. Minimizing the area of the image manifold leads to the Beltrami flow or mean curvature flow of the image surface in the 3D color space, while minimizing the elastica of the image surface yields an additional interesting regularization. Recently, the authors proposed a color elastica model, which minimizes both the surface area and elastica of the image manifold. In this paper, we propose to modify the color elastica and introduce two new models for color image regularization. The revised measures are motivated by the relations between the color elastica model, Euler's elastica model and the total variation model for gray level images. Compared to our previous color elastica model, the new models are direct extensions of Euler's elastica model to color images. The proposed models are nonlinear and challenging to minimize. To overcome this difficulty, two operator-splitting methods are suggested. Specifically, nonlinearities are decoupled by introducing new vector- and matrix-valued variables. Then, the minimization problems are converted to solving initial value problems which are time-discretized by operator splitting. Each subproblem, after splitting either, has a closed-form solution or can be solved efficiently. The effectiveness and advantages of the proposed models are demonstrated by comprehensive experiments. The benefits of incorporating the elastica of the image surface as regularization terms compared to common alternatives are empirically validated.
An Operator-Splitting Method for the Gaussian Curvature Regularization Model with Applications in Surface Smoothing and Imaging
Aug 04, 2021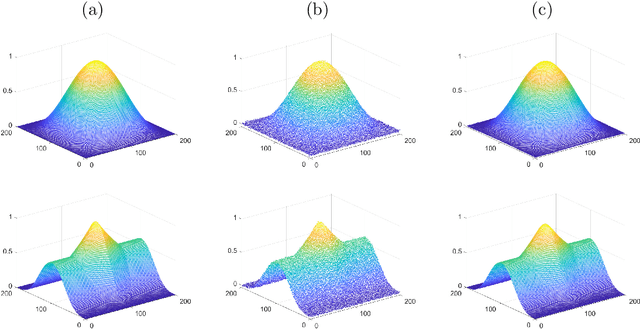

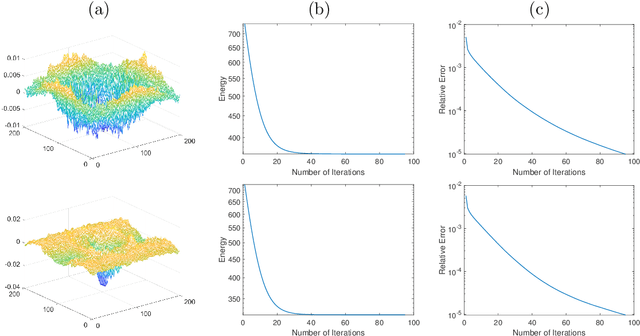
Abstract:Gaussian curvature is an important geometric property of surfaces, which has been used broadly in mathematical modeling. Due to the full nonlinearity of the Gaussian curvature, efficient numerical methods for models based on it are uncommon in literature. In this article, we propose an operator-splitting method for a general Gaussian curvature model. In our method, we decouple the full nonlinearity of Gaussian curvature from differential operators by introducing two matrix- and vector-valued functions. The optimization problem is then converted into the search for the steady state solution of a time dependent PDE system. The above PDE system is well-suited to time discretization by operator splitting, the sub-problems encountered at each fractional step having either a closed form solution or being solvable by efficient algorithms. The proposed method is not sensitive to the choice of parameters, its efficiency and performances being demonstrated via systematic experiments on surface smoothing and image denoising.
A Color Elastica Model for Vector-Valued Image Regularization
Aug 19, 2020

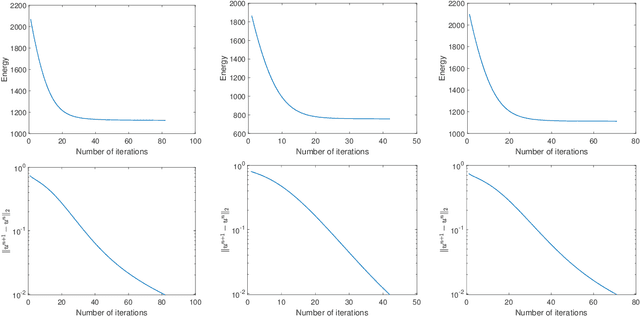

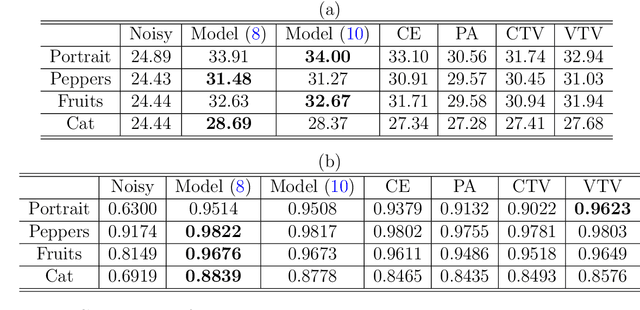
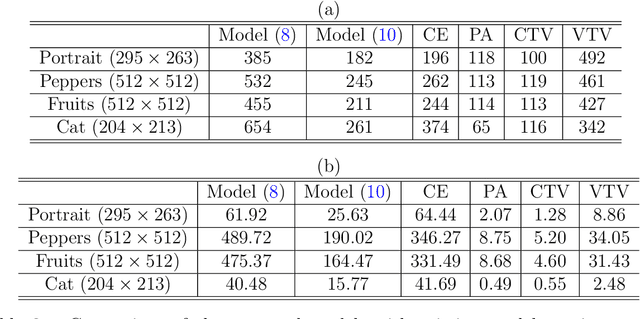
Abstract:Models related to the Euler's Elastica energy have proven to be very useful for many applications, including image processing and high energy physics. Extending the Elastica models to color images and multi-channel data is challenging, as numerical solvers for these geometric models are difficult to find. In the past, the Polyakov action from high energy physics has been successfully applied for color image processing. Like the single channel Euler's elastica model and the total variation (TV) models, measures that require high order derivatives could help when considering image formation models that minimize elastic properties, in one way or another. Here, we introduce an addition to the Polyakov action for color images that minimizes the color manifold curvature, that is computed by applying of the Laplace-Beltrami operator to the color image channels. When applied to gray scale images, while selecting appropriate scaling between space and color, the proposed model reduces to minimizing the Euler's Elastica operating on the image level sets. Finding a minimizer for the proposed nonlinear geometric model is the challenge we address in this paper. Specifically, we present an operator-splitting method to minimize the proposed functional. The nonlinearity is decoupled by introducing three vector-valued and matrix-valued variables. The problem is then converted into solving for the steady state of an associated initial-value problem. The initial-value problem is time-split into three fractional steps, such that each sub-problem has a closed form solution, or can be solved by fast algorithms. The efficiency, and robustness of the proposed method are demonstrated by systematic numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge