New region force for variational models in image segmentation and high dimensional data clustering
Paper and Code
Apr 26, 2017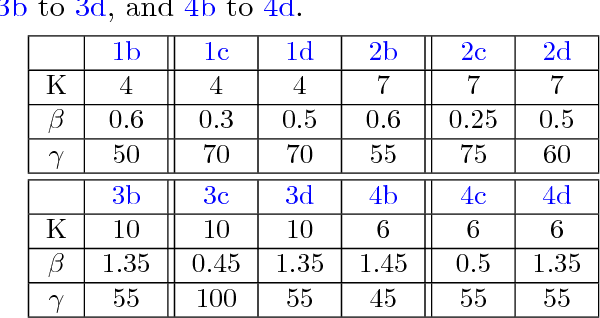
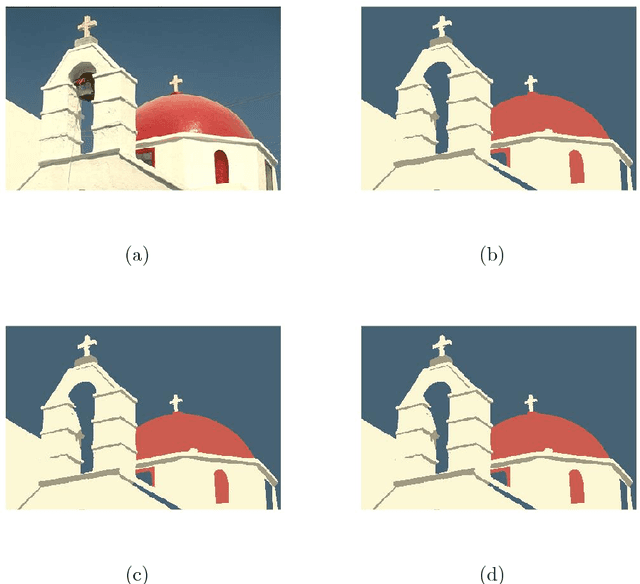

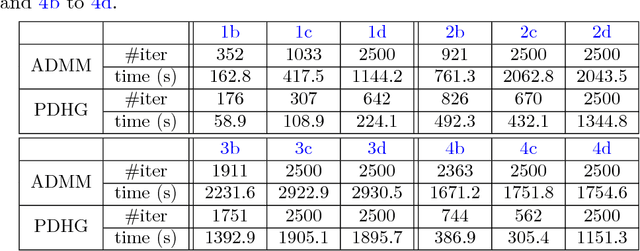
We propose an effective framework for multi-phase image segmentation and semi-supervised data clustering by introducing a novel region force term into the Potts model. Assume the probability that a pixel or a data point belongs to each class is known a priori. We show that the corresponding indicator function obeys the Bernoulli distribution and the new region force function can be computed as the negative log-likelihood function under the Bernoulli distribution. We solve the Potts model by the primal-dual hybrid gradient method and the augmented Lagrangian method, which are based on two different dual problems of the same primal problem. Empirical evaluations of the Potts model with the new region force function on benchmark problems show that it is competitive with existing variational methods in both image segmentation and semi-supervised data clustering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge