Dan Qiao
Policy-Conditioned Policies for Multi-Agent Task Solving
Dec 24, 2025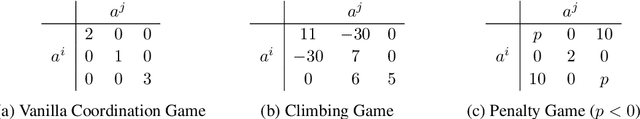

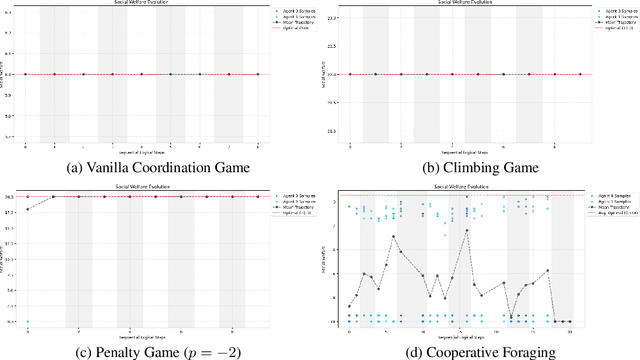
Abstract:In multi-agent tasks, the central challenge lies in the dynamic adaptation of strategies. However, directly conditioning on opponents' strategies is intractable in the prevalent deep reinforcement learning paradigm due to a fundamental ``representational bottleneck'': neural policies are opaque, high-dimensional parameter vectors that are incomprehensible to other agents. In this work, we propose a paradigm shift that bridges this gap by representing policies as human-interpretable source code and utilizing Large Language Models (LLMs) as approximate interpreters. This programmatic representation allows us to operationalize the game-theoretic concept of \textit{Program Equilibrium}. We reformulate the learning problem by utilizing LLMs to perform optimization directly in the space of programmatic policies. The LLM functions as a point-wise best-response operator that iteratively synthesizes and refines the ego agent's policy code to respond to the opponent's strategy. We formalize this process as \textit{Programmatic Iterated Best Response (PIBR)}, an algorithm where the policy code is optimized by textual gradients, using structured feedback derived from game utility and runtime unit tests. We demonstrate that this approach effectively solves several standard coordination matrix games and a cooperative Level-Based Foraging environment.
Stable Minima of ReLU Neural Networks Suffer from the Curse of Dimensionality: The Neural Shattering Phenomenon
Jun 25, 2025Abstract:We study the implicit bias of flatness / low (loss) curvature and its effects on generalization in two-layer overparameterized ReLU networks with multivariate inputs -- a problem well motivated by the minima stability and edge-of-stability phenomena in gradient-descent training. Existing work either requires interpolation or focuses only on univariate inputs. This paper presents new and somewhat surprising theoretical results for multivariate inputs. On two natural settings (1) generalization gap for flat solutions, and (2) mean-squared error (MSE) in nonparametric function estimation by stable minima, we prove upper and lower bounds, which establish that while flatness does imply generalization, the resulting rates of convergence necessarily deteriorate exponentially as the input dimension grows. This gives an exponential separation between the flat solutions vis-\`a-vis low-norm solutions (i.e., weight decay), which knowingly do not suffer from the curse of dimensionality. In particular, our minimax lower bound construction, based on a novel packing argument with boundary-localized ReLU neurons, reveals how flat solutions can exploit a kind of ''neural shattering'' where neurons rarely activate, but with high weight magnitudes. This leads to poor performance in high dimensions. We corroborate these theoretical findings with extensive numerical simulations. To the best of our knowledge, our analysis provides the first systematic explanation for why flat minima may fail to generalize in high dimensions.
Towards DS-NER: Unveiling and Addressing Latent Noise in Distant Annotations
May 18, 2025Abstract:Distantly supervised named entity recognition (DS-NER) has emerged as a cheap and convenient alternative to traditional human annotation methods, enabling the automatic generation of training data by aligning text with external resources. Despite the many efforts in noise measurement methods, few works focus on the latent noise distribution between different distant annotation methods. In this work, we explore the effectiveness and robustness of DS-NER by two aspects: (1) distant annotation techniques, which encompasses both traditional rule-based methods and the innovative large language model supervision approach, and (2) noise assessment, for which we introduce a novel framework. This framework addresses the challenges by distinctly categorizing them into the unlabeled-entity problem (UEP) and the noisy-entity problem (NEP), subsequently providing specialized solutions for each. Our proposed method achieves significant improvements on eight real-world distant supervision datasets originating from three different data sources and involving four distinct annotation techniques, confirming its superiority over current state-of-the-art methods.
No-Regret Linear Bandits under Gap-Adjusted Misspecification
Jan 09, 2025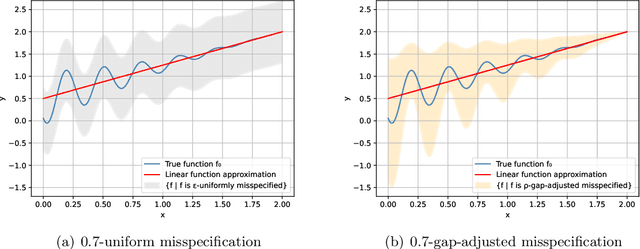
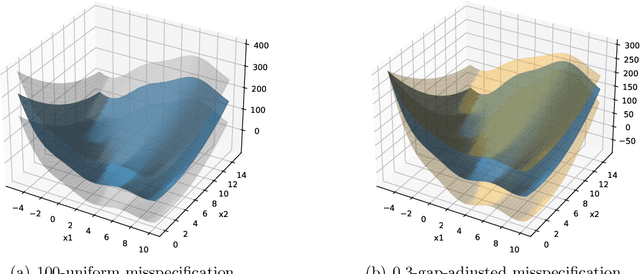
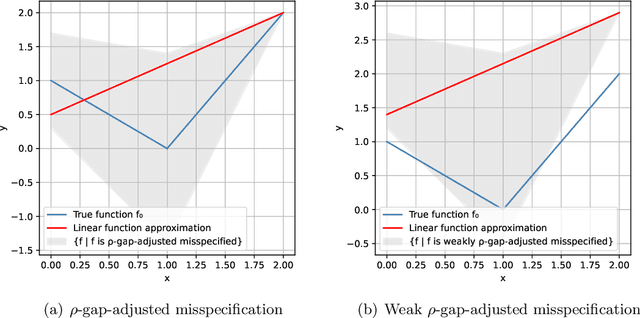
Abstract:This work studies linear bandits under a new notion of gap-adjusted misspecification and is an extension of Liu et al. (2023). When the underlying reward function is not linear, existing linear bandits work usually relies on a uniform misspecification parameter $\epsilon$ that measures the sup-norm error of the best linear approximation. This results in an unavoidable linear regret whenever $\epsilon > 0$. We propose a more natural model of misspecification which only requires the approximation error at each input $x$ to be proportional to the suboptimality gap at $x$. It captures the intuition that, for optimization problems, near-optimal regions should matter more and we can tolerate larger approximation errors in suboptimal regions. Quite surprisingly, we show that the classical LinUCB algorithm -- designed for the realizable case -- is automatically robust against such $\rho$-gap-adjusted misspecification with parameter $\rho$ diminishing at $O(1/(d \sqrt{\log T}))$. It achieves a near-optimal $O(\sqrt{T})$ regret for problems that the best-known regret is almost linear in time horizon $T$. We further advance this frontier by presenting a novel phased elimination-based algorithm whose gap-adjusted misspecification parameter $\rho = O(1/\sqrt{d})$ does not scale with $T$. This algorithm attains optimal $O(\sqrt{T})$ regret and is deployment-efficient, requiring only $\log T$ batches of exploration. It also enjoys an adaptive $O(\log T)$ regret when a constant suboptimality gap exists. Technically, our proof relies on a novel self-bounding argument that bounds the part of the regret due to misspecification by the regret itself, and a new inductive lemma that limits the misspecification error within the suboptimality gap for all valid actions in each batch selected by G-optimal design.
Stable Minima Cannot Overfit in Univariate ReLU Networks: Generalization by Large Step Sizes
Jun 10, 2024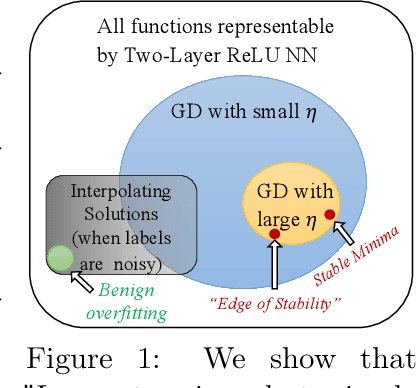
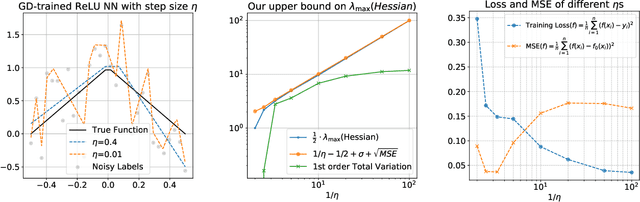
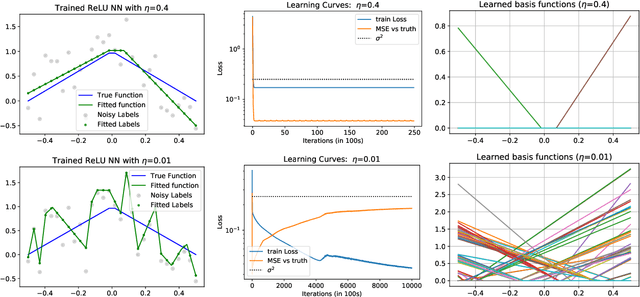
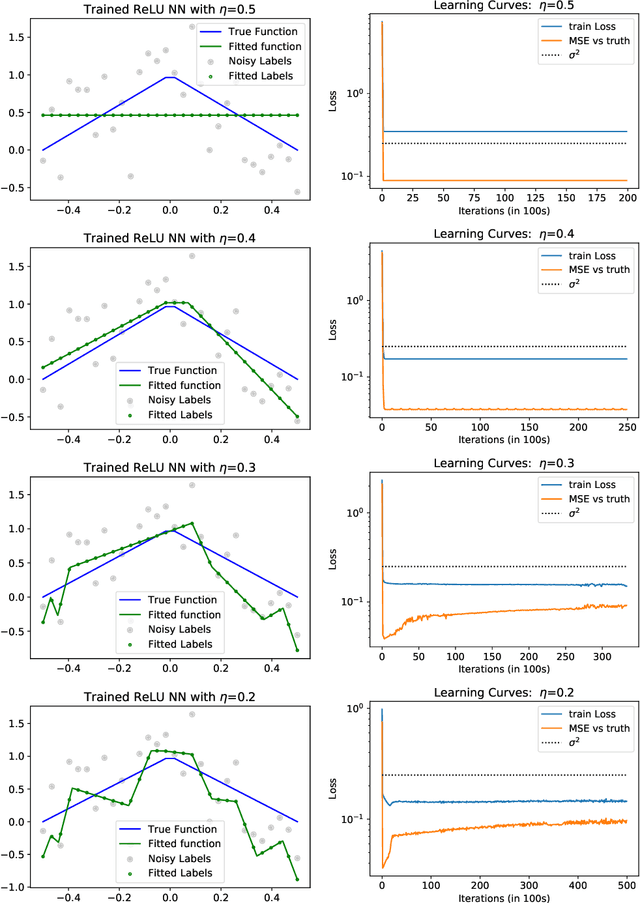
Abstract:We study the generalization of two-layer ReLU neural networks in a univariate nonparametric regression problem with noisy labels. This is a problem where kernels (\emph{e.g.} NTK) are provably sub-optimal and benign overfitting does not happen, thus disqualifying existing theory for interpolating (0-loss, global optimal) solutions. We present a new theory of generalization for local minima that gradient descent with a constant learning rate can \emph{stably} converge to. We show that gradient descent with a fixed learning rate $\eta$ can only find local minima that represent smooth functions with a certain weighted \emph{first order total variation} bounded by $1/\eta - 1/2 + \widetilde{O}(\sigma + \sqrt{\mathrm{MSE}})$ where $\sigma$ is the label noise level, $\mathrm{MSE}$ is short for mean squared error against the ground truth, and $\widetilde{O}(\cdot)$ hides a logarithmic factor. Under mild assumptions, we also prove a nearly-optimal MSE bound of $\widetilde{O}(n^{-4/5})$ within the strict interior of the support of the $n$ data points. Our theoretical results are validated by extensive simulation that demonstrates large learning rate training induces sparse linear spline fits. To the best of our knowledge, we are the first to obtain generalization bound via minima stability in the non-interpolation case and the first to show ReLU NNs without regularization can achieve near-optimal rates in nonparametric regression.
OpenBA-V2: Reaching 77.3% High Compression Ratio with Fast Multi-Stage Pruning
May 09, 2024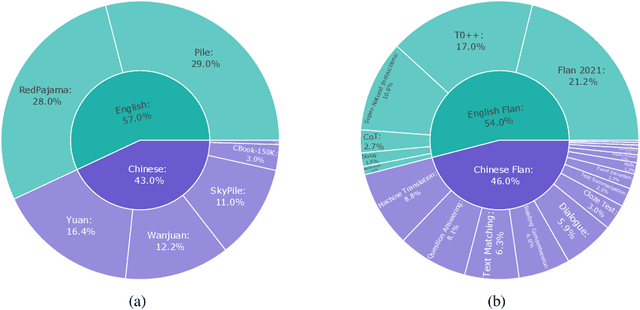

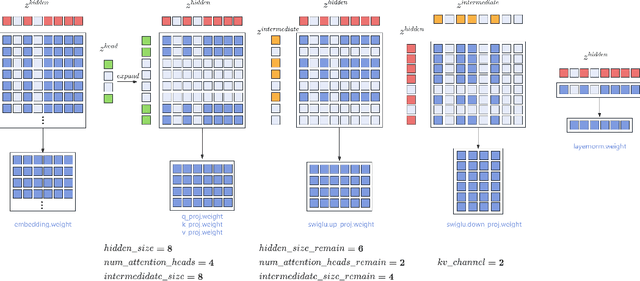
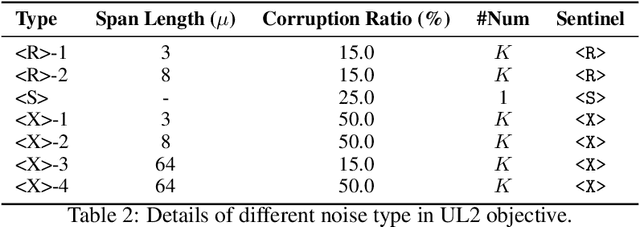
Abstract:Large Language Models (LLMs) have played an important role in many fields due to their powerful capabilities.However, their massive number of parameters leads to high deployment requirements and incurs significant inference costs, which impedes their practical applications. Training smaller models is an effective way to address this problem. Therefore, we introduce OpenBA-V2, a 3.4B model derived from multi-stage compression and continual pre-training from the original 15B OpenBA model. OpenBA-V2 utilizes more data, more flexible training objectives, and techniques such as layer pruning, neural pruning, and vocabulary pruning to achieve a compression rate of 77.3\% with minimal performance loss. OpenBA-V2 demonstrates competitive performance compared to other open-source models of similar size, achieving results close to or on par with the 15B OpenBA model in downstream tasks such as common sense reasoning and Named Entity Recognition (NER). OpenBA-V2 illustrates that LLMs can be compressed into smaller ones with minimal performance loss by employing advanced training objectives and data strategies, which may help deploy LLMs in resource-limited scenarios.
Differentially Private Reinforcement Learning with Self-Play
Apr 11, 2024Abstract:We study the problem of multi-agent reinforcement learning (multi-agent RL) with differential privacy (DP) constraints. This is well-motivated by various real-world applications involving sensitive data, where it is critical to protect users' private information. We first extend the definitions of Joint DP (JDP) and Local DP (LDP) to two-player zero-sum episodic Markov Games, where both definitions ensure trajectory-wise privacy protection. Then we design a provably efficient algorithm based on optimistic Nash value iteration and privatization of Bernstein-type bonuses. The algorithm is able to satisfy JDP and LDP requirements when instantiated with appropriate privacy mechanisms. Furthermore, for both notions of DP, our regret bound generalizes the best known result under the single-agent RL case, while our regret could also reduce to the best known result for multi-agent RL without privacy constraints. To the best of our knowledge, these are the first line of results towards understanding trajectory-wise privacy protection in multi-agent RL.
Near-Optimal Reinforcement Learning with Self-Play under Adaptivity Constraints
Feb 02, 2024
Abstract:We study the problem of multi-agent reinforcement learning (MARL) with adaptivity constraints -- a new problem motivated by real-world applications where deployments of new policies are costly and the number of policy updates must be minimized. For two-player zero-sum Markov Games, we design a (policy) elimination based algorithm that achieves a regret of $\widetilde{O}(\sqrt{H^3 S^2 ABK})$, while the batch complexity is only $O(H+\log\log K)$. In the above, $S$ denotes the number of states, $A,B$ are the number of actions for the two players respectively, $H$ is the horizon and $K$ is the number of episodes. Furthermore, we prove a batch complexity lower bound $\Omega(\frac{H}{\log_{A}K}+\log\log K)$ for all algorithms with $\widetilde{O}(\sqrt{K})$ regret bound, which matches our upper bound up to logarithmic factors. As a byproduct, our techniques naturally extend to learning bandit games and reward-free MARL within near optimal batch complexity. To the best of our knowledge, these are the first line of results towards understanding MARL with low adaptivity.
OpenBA: An Open-sourced 15B Bilingual Asymmetric seq2seq Model Pre-trained from Scratch
Oct 01, 2023



Abstract:Large language models (LLMs) with billions of parameters have demonstrated outstanding performance on various natural language processing tasks. This report presents OpenBA, an open-sourced 15B bilingual asymmetric seq2seq model, to contribute an LLM variant to the Chinese-oriented open-source model community. We enhance OpenBA with effective and efficient techniques as well as adopt a three-stage training strategy to train the model from scratch. Our solution can also achieve very competitive performance with only 380B tokens, which is better than LLaMA-70B on the BELEBELE benchmark, BLOOM-176B on the MMLU benchmark, GLM-130B on the C-Eval (hard) benchmark. This report provides the main details to pre-train an analogous model, including pre-training data processing, Bilingual Flan data collection, the empirical observations that inspire our model architecture design, training objectives of different stages, and other enhancement techniques. Additionally, we also provide the fine-tuning details of OpenBA on four downstream tasks. We have refactored our code to follow the design principles of the Huggingface Transformers Library, making it more convenient for developers to use, and released checkpoints of different training stages at https://huggingface.co/openBA. More details of our project are available at https://github.com/OpenNLG/openBA.git.
GameEval: Evaluating LLMs on Conversational Games
Aug 19, 2023Abstract:The rapid advancements in large language models (LLMs) have presented challenges in evaluating those models. Existing evaluation methods are either reference-based or preference based, which inevitably need human intervention or introduce test bias caused by evaluator models. In this paper, we propose GameEval, a novel approach to evaluating LLMs through goal-driven conversational games, overcoming the limitations of previous methods. GameEval treats LLMs as game players and assigns them distinct roles with specific goals achieved by launching conversations of various forms, including discussion, question answering, and voting. We design three unique games with cooperative or adversarial objectives, accompanied by corresponding evaluation metrics, to show how this new paradigm comprehensively evaluates model performance.Through extensive experiments, we show that GameEval can effectively differentiate the capabilities of various LLMs, providing a comprehensive assessment of their integrated abilities to solve complex problems. Our public anonymous code is available at https://github.com/GameEval/GameEval.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge