LoLA: Low-Rank Linear Attention With Sparse Caching

Transformer-based large language models suffer from quadratic complexity at inference on long sequences. Linear attention methods are efficient alternatives, however, they fail to provide an accurate approximation of softmax attention. By additionally incorporating sliding window attention into each linear attention head, this gap can be closed for short context-length tasks. Unfortunately, these approaches cannot recall important information from long contexts due to "memory collisions". In this paper , we propose LoLA: Low-rank Linear Attention with sparse caching. LoLA separately stores additional key-value pairs that would otherwise interfere with past associative memories. Moreover, LoLA further closes the gap between linear attention models and transformers by distributing past key-value pairs into three forms of memory: (i) recent pairs in a local sliding window; (ii) difficult-to-memorize pairs in a sparse, global cache; and (iii) generic pairs in the recurrent hidden state of linear attention. As an inference-only strategy, LoLA enables pass-key retrieval on up to 8K context lengths on needle-in-a-haystack tasks from RULER. It boosts the accuracy of the base subquadratic model from 0.6% to 97.4% at 4K context lengths, with a 4.6x smaller cache than that of Llama-3.1 8B. LoLA demonstrates strong performance on zero-shot commonsense reasoning tasks among 1B and 8B parameter subquadratic models. Finally, LoLA is an extremely lightweight approach: Nearly all of our results can be reproduced on a single consumer GPU.

Optimal Recovery Meets Minimax Estimation

A fundamental problem in statistics and machine learning is to estimate a function $f$ from possibly noisy observations of its point samples. The goal is to design a numerical algorithm to construct an approximation $\hat f$ to $f$ in a prescribed norm that asymptotically achieves the best possible error (as a function of the number $m$ of observations and the variance $\sigma^2$ of the noise). This problem has received considerable attention in both nonparametric statistics (noisy observations) and optimal recovery (noiseless observations). Quantitative bounds require assumptions on $f$, known as model class assumptions. Classical results assume that $f$ is in the unit ball of a Besov space. In nonparametric statistics, the best possible performance of an algorithm for finding $\hat f$ is known as the minimax rate and has been studied in this setting under the assumption that the noise is Gaussian. In optimal recovery, the best possible performance of an algorithm is known as the optimal recovery rate and has also been determined in this setting. While one would expect that the minimax rate recovers the optimal recovery rate when the noise level $\sigma$ tends to zero, it turns out that the current results on minimax rates do not carefully determine the dependence on $\sigma$ and the limit cannot be taken. This paper handles this issue and determines the noise-level-aware (NLA) minimax rates for Besov classes when error is measured in an $L_q$-norm with matching upper and lower bounds. The end result is a reconciliation between minimax rates and optimal recovery rates. The NLA minimax rate continuously depends on the noise level and recovers the optimal recovery rate when $\sigma$ tends to zero.

A Gap Between the Gaussian RKHS and Neural Networks: An Infinite-Center Asymptotic Analysis

Recent works have characterized the function-space inductive bias of infinite-width bounded-norm single-hidden-layer neural networks as a kind of bounded-variation-type space. This novel neural network Banach space encompasses many classical multivariate function spaces including certain Sobolev spaces and the spectral Barron spaces. Notably, this Banach space also includes functions that exhibit less classical regularity such as those that only vary in a few directions. On bounded domains, it is well-established that the Gaussian reproducing kernel Hilbert space (RKHS) strictly embeds into this Banach space, demonstrating a clear gap between the Gaussian RKHS and the neural network Banach space. It turns out that when investigating these spaces on unbounded domains, e.g., all of $\mathbb{R}^d$, the story is fundamentally different. We establish the following fundamental result: Certain functions that lie in the Gaussian RKHS have infinite norm in the neural network Banach space. This provides a nontrivial gap between kernel methods and neural networks by the exhibition of functions in which kernel methods can do strictly better than neural networks.

Random ReLU Neural Networks as Non-Gaussian Processes

We consider a large class of shallow neural networks with randomly initialized parameters and rectified linear unit activation functions. We prove that these random neural networks are well-defined non-Gaussian processes. As a by-product, we demonstrate that these networks are solutions to stochastic differential equations driven by impulsive white noise (combinations of random Dirac measures). These processes are parameterized by the law of the weights and biases as well as the density of activation thresholds in each bounded region of the input domain. We prove that these processes are isotropic and wide-sense self-similar with Hurst exponent $3/2$. We also derive a remarkably simple closed-form expression for their autocovariance function. Our results are fundamentally different from prior work in that we consider a non-asymptotic viewpoint: The number of neurons in each bounded region of the input domain (i.e., the width) is itself a random variable with a Poisson law with mean proportional to the density parameter. Finally, we show that, under suitable hypotheses, as the expected width tends to infinity, these processes can converge in law not only to Gaussian processes, but also to non-Gaussian processes depending on the law of the weights. Our asymptotic results provide a new take on several classical results (wide networks converge to Gaussian processes) as well as some new ones (wide networks can converge to non-Gaussian processes).

Banach Space Optimality of Neural Architectures With Multivariate Nonlinearities

We investigate the variational optimality (specifically, the Banach space optimality) of a large class of neural architectures with multivariate nonlinearities/activation functions. To that end, we construct a new family of Banach spaces defined via a regularization operator and the $k$-plane transform. We prove a representer theorem that states that the solution sets to learning problems posed over these Banach spaces are completely characterized by neural architectures with multivariate nonlinearities. These optimal architectures have skip connections and are tightly connected to orthogonal weight normalization and multi-index models, both of which have received considerable interest in the neural network community. Our framework is compatible with a number of classical nonlinearities including the rectified linear unit (ReLU) activation function, the norm activation function, and the radial basis functions found in the theory of thin-plate/polyharmonic splines. We also show that the underlying spaces are special instances of reproducing kernel Banach spaces and variation spaces. Our results shed light on the regularity of functions learned by neural networks trained on data, particularly with multivariate nonlinearities, and provide new theoretical motivation for several architectural choices found in practice.

Weighted variation spaces and approximation by shallow ReLU networks

We investigate the approximation of functions $f$ on a bounded domain $\Omega\subset \mathbb{R}^d$ by the outputs of single-hidden-layer ReLU neural networks of width $n$. This form of nonlinear $n$-term dictionary approximation has been intensely studied since it is the simplest case of neural network approximation (NNA). There are several celebrated approximation results for this form of NNA that introduce novel model classes of functions on $\Omega$ whose approximation rates avoid the curse of dimensionality. These novel classes include Barron classes, and classes based on sparsity or variation such as the Radon-domain BV classes. The present paper is concerned with the definition of these novel model classes on domains $\Omega$. The current definition of these model classes does not depend on the domain $\Omega$. A new and more proper definition of model classes on domains is given by introducing the concept of weighted variation spaces. These new model classes are intrinsic to the domain itself. The importance of these new model classes is that they are strictly larger than the classical (domain-independent) classes. Yet, it is shown that they maintain the same NNA rates.

Vector-Valued Variation Spaces and Width Bounds for DNNs: Insights on Weight Decay Regularization

Deep neural networks (DNNs) trained to minimize a loss term plus the sum of squared weights via gradient descent corresponds to the common approach of training with weight decay. This paper provides new insights into this common learning framework. We characterize the kinds of functions learned by training with weight decay for multi-output (vector-valued) ReLU neural networks. This extends previous characterizations that were limited to single-output (scalar-valued) networks. This characterization requires the definition of a new class of neural function spaces that we call vector-valued variation (VV) spaces. We prove that neural networks (NNs) are optimal solutions to learning problems posed over VV spaces via a novel representer theorem. This new representer theorem shows that solutions to these learning problems exist as vector-valued neural networks with widths bounded in terms of the number of training data. Next, via a novel connection to the multi-task lasso problem, we derive new and tighter bounds on the widths of homogeneous layers in DNNs. The bounds are determined by the effective dimensions of the training data embeddings in/out of the layers. This result sheds new light on the architectural requirements for DNNs. Finally, the connection to the multi-task lasso problem suggests a new approach to compressing pre-trained networks.

Deep Learning Meets Sparse Regularization: A Signal Processing Perspective

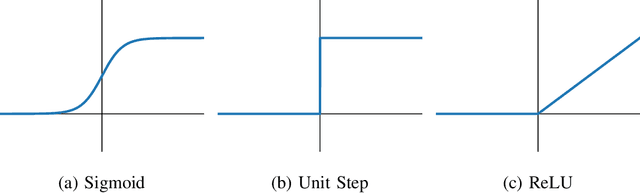
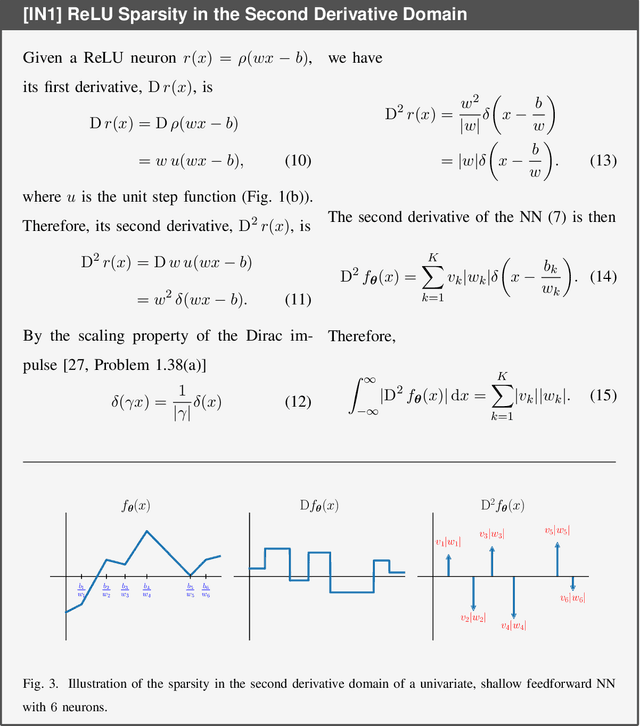
Deep learning has been wildly successful in practice and most state-of-the-art machine learning methods are based on neural networks. Lacking, however, is a rigorous mathematical theory that adequately explains the amazing performance of deep neural networks. In this article, we present a relatively new mathematical framework that provides the beginning of a deeper understanding of deep learning. This framework precisely characterizes the functional properties of neural networks that are trained to fit to data. The key mathematical tools which support this framework include transform-domain sparse regularization, the Radon transform of computed tomography, and approximation theory, which are all techniques deeply rooted in signal processing. This framework explains the effect of weight decay regularization in neural network training, the use of skip connections and low-rank weight matrices in network architectures, the role of sparsity in neural networks, and explains why neural networks can perform well in high-dimensional problems.

Near-Minimax Optimal Estimation With Shallow ReLU Neural Networks

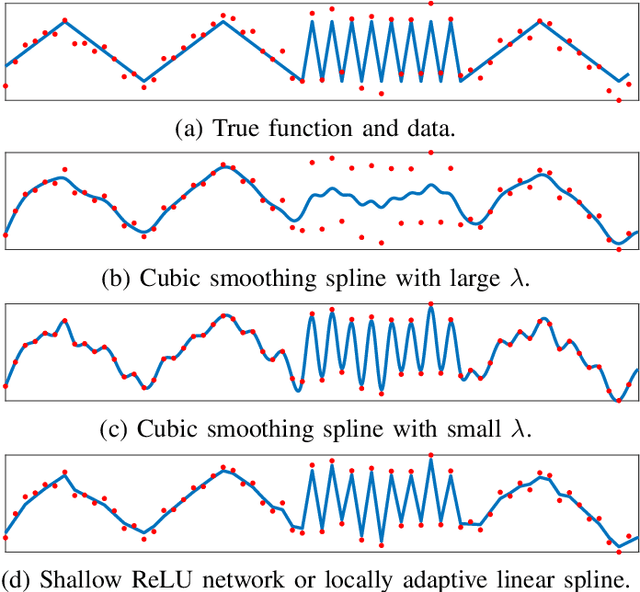
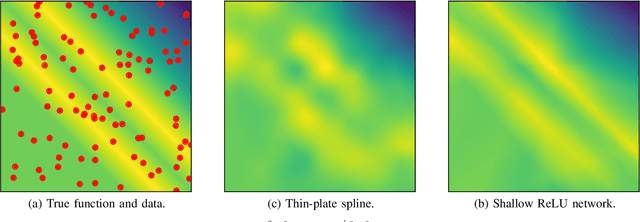
We study the problem of estimating an unknown function from noisy data using shallow (single-hidden layer) ReLU neural networks. The estimators we study minimize the sum of squared data-fitting errors plus a regularization term proportional to the Euclidean norm of the network weights. This minimization corresponds to the common approach of training a neural network with weight decay. We quantify the performance (mean-squared error) of these neural network estimators when the data-generating function belongs to the space of functions of second-order bounded variation in the Radon domain. This space of functions was recently proposed as the natural function space associated with shallow ReLU neural networks. We derive a minimax lower bound for the estimation problem for this function space and show that the neural network estimators are minimax optimal up to logarithmic factors. We also show that this is a "mixed variation" function space that contains classical multivariate function spaces including certain Sobolev spaces and certain spectral Barron spaces. Finally, we use these results to quantify a gap between neural networks and linear methods (which include kernel methods). This paper sheds light on the phenomenon that neural networks seem to break the curse of dimensionality.

What Kinds of Functions do Deep Neural Networks Learn? Insights from Variational Spline Theory

We develop a variational framework to understand the properties of functions learned by deep neural networks with ReLU activation functions fit to data. We propose a new function space, which is reminiscent of classical bounded variation spaces, that captures the compositional structure associated with deep neural networks. We derive a representer theorem showing that deep ReLU networks are solutions to regularized data fitting problems in this function space. The function space consists of compositions of functions from the (non-reflexive) Banach spaces of second-order bounded variation in the Radon domain. These are Banach spaces with sparsity-promoting norms, giving insight into the role of sparsity in deep neural networks. The neural network solutions have skip connections and rank bounded weight matrices, providing new theoretical support for these common architectural choices. The variational problem we study can be recast as a finite-dimensional neural network training problem with regularization schemes related to the notions of weight decay and path-norm regularization. Finally, our analysis builds on techniques from variational spline theory, providing new connections between deep neural networks and splines.