All You Need is Resistance: On the Equivalence of Effective Resistance and Certain Optimal Transport Problems on Graphs

The fields of effective resistance and optimal transport on graphs are filled with rich connections to combinatorics, geometry, machine learning, and beyond. In this article we put forth a bold claim: that the two fields should be understood as one and the same, up to a choice of $p$. We make this claim precise by introducing the parameterized family of $p$-Beckmann distances for probability measures on graphs and relate them sharply to certain Wasserstein distances. Then, we break open a suite of results including explicit connections to optimal stopping times and random walks on graphs, graph Sobolev spaces, and a Benamou-Brenier type formula for $2$-Beckmann distance. We further explore empirical implications in the world of unsupervised learning for graph data and propose further study of the usage of these metrics where Wasserstein distance may produce computational bottlenecks.

Comparing Graph Transformers via Positional Encodings

The distinguishing power of graph transformers is closely tied to the choice of positional encoding: features used to augment the base transformer with information about the graph. There are two primary types of positional encoding: absolute positional encodings (APEs) and relative positional encodings (RPEs). APEs assign features to each node and are given as input to the transformer. RPEs instead assign a feature to each pair of nodes, e.g., graph distance, and are used to augment the attention block. A priori, it is unclear which method is better for maximizing the power of the resulting graph transformer. In this paper, we aim to understand the relationship between these different types of positional encodings. Interestingly, we show that graph transformers using APEs and RPEs are equivalent in terms of distinguishing power. In particular, we demonstrate how to interchange APEs and RPEs while maintaining their distinguishing power in terms of graph transformers. Based on our theoretical results, we provide a study on several APEs and RPEs (including the resistance distance and the recently introduced stable and expressive positional encoding (SPE)) and compare their distinguishing power in terms of transformers. We believe our work will help navigate the huge number of choices of positional encoding and will provide guidance on the future design of positional encodings for graph transformers.

Distances for Markov Chains, and Their Differentiation

(Directed) graphs with node attributes are a common type of data in various applications and there is a vast literature on developing metrics and efficient algorithms for comparing them. Recently, in the graph learning and optimization communities, a range of new approaches have been developed for comparing graphs with node attributes, leveraging ideas such as the Optimal Transport (OT) and the Weisfeiler-Lehman (WL) graph isomorphism test. Two state-of-the-art representatives are the OTC distance proposed by O'Connor et al., 2022 and the WL distance by Chen et al.,2022. Interestingly, while these two distances are developed based on different ideas, we observe that they both view graphs as Markov chains, and are deeply connected. Indeed, in this paper, we propose a unified framework to generate distances for Markov chains (thus including (directed) graphs with node attributes), which we call the Optimal Transport Markov (OTM) distances, that encompass both the OTC and the WL distances. We further introduce a special one-parameter family of distances within our OTM framework, called the discounted WL distance. We show that the discounted WL distance has nice theoretical properties and can address several limitations of the existing OTC and WL distances. Furthermore, contrary to the OTC and the WL distances, we show our new discounted WL distance can be differentiated (after an entropy-regularization similar to the Sinkhorn distance), making it suitable for use in learning frameworks, e.g., as the reconstruction loss in a graph generative model.

Understanding Oversquashing in GNNs through the Lens of Effective Resistance

Message passing graph neural networks are popular learning architectures for graph-structured data. However, it can be challenging for them to capture long range interactions in graphs. One of the potential reasons is the so-called oversquashing problem, first termed in [Alon and Yahav, 2020], that has recently received significant attention. In this paper, we analyze the oversquashing problem through the lens of effective resistance between nodes in the input graphs. The concept of effective resistance intuitively captures the "strength" of connection between two nodes by paths in the graph, and has a rich literature connecting spectral graph theory and circuit networks theory. We propose the use the concept of total effective resistance as a measure to quantify the total amount of oversquashing in a graph, and provide theoretical justification of its use. We further develop algorithms to identify edges to be added to an input graph so as to minimize the total effective resistance, thereby alleviating the oversquashing problem when using GNNs. We provide empirical evidence of the effectiveness of our total effective resistance based rewiring strategies.

The Weisfeiler-Lehman Distance: Reinterpretation and Connection with GNNs

In this paper, we present a novel interpretation of the so-called Weisfeiler-Lehman (WL) distance, introduced by Chen et al. (2022), using concepts from stochastic processes. The WL distance aims at comparing graphs with node features, has the same discriminative power as the classic Weisfeiler-Lehman graph isomorphism test and has deep connections to the Gromov-Wasserstein distance. This new interpretation connects the WL distance to the literature on distances for stochastic processes, which also makes the interpretation of the distance more accessible and intuitive. We further explore the connections between the WL distance and certain Message Passing Neural Networks, and discuss the implications of the WL distance for understanding the Lipschitz property and the universal approximation results for these networks.

The Numerical Stability of Hyperbolic Representation Learning

Given the exponential growth of the volume of the ball w.r.t. its radius, the hyperbolic space is capable of embedding trees with arbitrarily small distortion and hence has received wide attention for representing hierarchical datasets. However, this exponential growth property comes at a price of numerical instability such that training hyperbolic learning models will sometimes lead to catastrophic NaN problems, encountering unrepresentable values in floating point arithmetic. In this work, we carefully analyze the limitation of two popular models for the hyperbolic space, namely, the Poincar\'e ball and the Lorentz model. We first show that, under the 64 bit arithmetic system, the Poincar\'e ball has a relatively larger capacity than the Lorentz model for correctly representing points. Then, we theoretically validate the superiority of the Lorentz model over the Poincar\'e ball from the perspective of optimization. Given the numerical limitations of both models, we identify one Euclidean parametrization of the hyperbolic space which can alleviate these limitations. We further extend this Euclidean parametrization to hyperbolic hyperplanes and exhibits its ability in improving the performance of hyperbolic SVM.

Weisfeiler-Lehman meets Gromov-Wasserstein

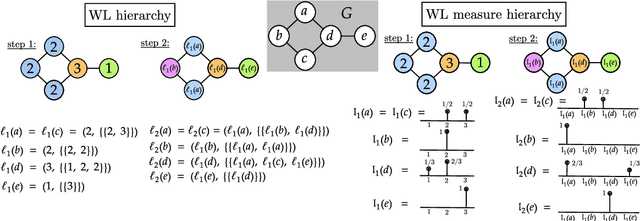
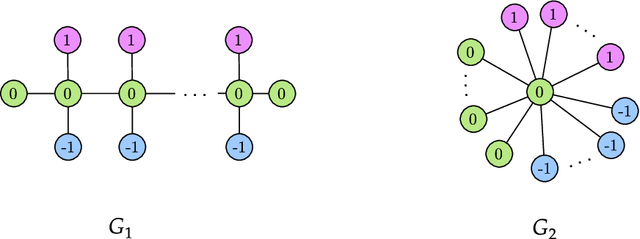
The Weisfeiler-Lehman (WL) test is a classical procedure for graph isomorphism testing. The WL test has also been widely used both for designing graph kernels and for analyzing graph neural networks. In this paper, we propose the Weisfeiler-Lehman (WL) distance, a notion of distance between labeled measure Markov chains (LMMCs), of which labeled graphs are special cases. The WL distance is polynomial time computable and is also compatible with the WL test in the sense that the former is positive if and only if the WL test can distinguish the two involved graphs. The WL distance captures and compares subtle structures of the underlying LMMCs and, as a consequence of this, it is more discriminating than the distance between graphs used for defining the state-of-the-art Wasserstein Weisfeiler-Lehman graph kernel. Inspired by the structure of the WL distance we identify a neural network architecture on LMMCs which turns out to be universal w.r.t. continuous functions defined on the space of all LMMCs (which includes all graphs) endowed with the WL distance. Finally, the WL distance turns out to be stable w.r.t. a natural variant of the Gromov-Wasserstein (GW) distance for comparing metric Markov chains that we identify. Hence, the WL distance can also be construed as a polynomial time lower bound for the GW distance which is in general NP-hard to compute.

The Gaussian Transform

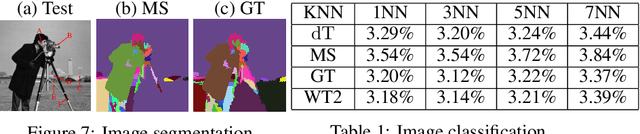
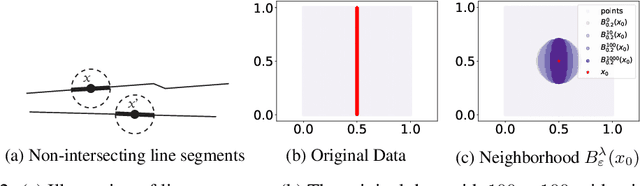
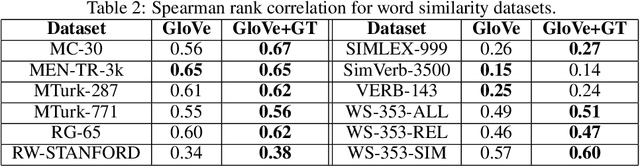
We introduce the Gaussian transform (GT), an optimal transport inspired iterative method for denoising and enhancing latent structures in datasets. Under the hood, GT generates a new distance function (GT distance) on a given dataset by computing the $\ell^2$-Wasserstein distance between certain Gaussian density estimates obtained by localizing the dataset to individual points. Our contribution is twofold: (1) theoretically, we establish firstly that GT is stable under perturbations and secondly that in the continuous case, each point possesses an asymptotically ellipsoidal neighborhood with respect to the GT distance; (2) computationally, we accelerate GT both by identifying a strategy for reducing the number of matrix square root computations inherent to the $\ell^2$-Wasserstein distance between Gaussian measures, and by avoiding redundant computations of GT distances between points via enhanced neighborhood mechanisms. We also observe that GT is both a generalization and a strengthening of the mean shift (MS) method, and it is also a computationally efficient specialization of the recently proposed Wasserstein Transform (WT) method. We perform extensive experimentation comparing their performance in different scenarios.

The Wasserstein transform

We introduce the Wasserstein transform, a method for enhancing and denoising datasets defined on general metric spaces. The construction draws inspiration from Optimal Transportation ideas. We establish precise connections with the mean shift family of algorithms and establish the stability of both our method and mean shift under data perturbation.