Efficient and Stable Multi-Dimensional Kolmogorov-Smirnov Distance

We revisit extending the Kolmogorov-Smirnov distance between probability distributions to the multidimensional setting and make new arguments about the proper way to approach this generalization. Our proposed formulation maximizes the difference over orthogonal dominating rectangular ranges (d-sided rectangles in R^d), and is an integral probability metric. We also prove that the distance between a distribution and a sample from the distribution converges to 0 as the sample size grows, and bound this rate. Moreover, we show that one can, up to this same approximation error, compute the distance efficiently in 4 or fewer dimensions; specifically the runtime is near-linear in the size of the sample needed for that error. With this, we derive a delta-precision two-sample hypothesis test using this distance. Finally, we show these metric and approximation properties do not hold for other popular variants.

No Dimensional Sampling Coresets for Classification

We refine and generalize what is known about coresets for classification problems via the sensitivity sampling framework. Such coresets seek the smallest possible subsets of input data, so one can optimize a loss function on the coreset and ensure approximation guarantees with respect to the original data. Our analysis provides the first no dimensional coresets, so the size does not depend on the dimension. Moreover, our results are general, apply for distributional input and can use iid samples, so provide sample complexity bounds, and work for a variety of loss functions. A key tool we develop is a Radamacher complexity version of the main sensitivity sampling approach, which can be of independent interest.

On Mergable Coresets for Polytope Distance

We show that a constant-size constant-error coreset for polytope distance is simple to maintain under merges of coresets. However, increasing the size cannot improve the error bound significantly beyond that constant.

Sketching Multidimensional Time Series for Fast Discord Mining

Time series discords are a useful primitive for time series anomaly detection, and the matrix profile is capable of capturing discord effectively. There exist many research efforts to improve the scalability of discord discovery with respect to the length of time series. However, there is surprisingly little work focused on reducing the time complexity of matrix profile computation associated with dimensionality of a multidimensional time series. In this work, we propose a sketch for discord mining among multi-dimensional time series. After an initial pre-processing of the sketch as fast as reading the data, the discord mining has runtime independent of the dimensionality of the original data. On several real world examples from water treatment and transportation, the proposed algorithm improves the throughput by at least an order of magnitude (50X) and only has minimal impact on the quality of the approximated solution. Additionally, the proposed method can handle the dynamic addition or deletion of dimensions inconsequential overhead. This allows a data analyst to consider "what-if" scenarios in real time while exploring the data.

An Efficient Content-based Time Series Retrieval System

A Content-based Time Series Retrieval (CTSR) system is an information retrieval system for users to interact with time series emerged from multiple domains, such as finance, healthcare, and manufacturing. For example, users seeking to learn more about the source of a time series can submit the time series as a query to the CTSR system and retrieve a list of relevant time series with associated metadata. By analyzing the retrieved metadata, users can gather more information about the source of the time series. Because the CTSR system is required to work with time series data from diverse domains, it needs a high-capacity model to effectively measure the similarity between different time series. On top of that, the model within the CTSR system has to compute the similarity scores in an efficient manner as the users interact with the system in real-time. In this paper, we propose an effective and efficient CTSR model that outperforms alternative models, while still providing reasonable inference runtimes. To demonstrate the capability of the proposed method in solving business problems, we compare it against alternative models using our in-house transaction data. Our findings reveal that the proposed model is the most suitable solution compared to others for our transaction data problem.

For Kernel Range Spaces a Constant Number of Queries Are Sufficient

We introduce the notion of an $\varepsilon$-cover for a kernel range space. A kernel range space concerns a set of points $X \subset \mathbb{R}^d$ and the space of all queries by a fixed kernel (e.g., a Gaussian kernel $K(p,\cdot) = \exp(-\|p-\cdot\|^2)$). For a point set $X$ of size $n$, a query returns a vector of values $R_p \in \mathbb{R}^n$, where the $i$th coordinate $(R_p)_i = K(p,x_i)$ for $x_i \in X$. An $\varepsilon$-cover is a subset of points $Q \subset \mathbb{R}^d$ so for any $p \in \mathbb{R}^d$ that $\frac{1}{n} \|R_p - R_q\|_1\leq \varepsilon$ for some $q \in Q$. This is a smooth analog of Haussler's notion of $\varepsilon$-covers for combinatorial range spaces (e.g., defined by subsets of points within a ball query) where the resulting vectors $R_p$ are in $\{0,1\}^n$ instead of $[0,1]^n$. The kernel versions of these range spaces show up in data analysis tasks where the coordinates may be uncertain or imprecise, and hence one wishes to add some flexibility in the notion of inside and outside of a query range. Our main result is that, unlike combinatorial range spaces, the size of kernel $\varepsilon$-covers is independent of the input size $n$ and dimension $d$. We obtain a bound of $(1/\varepsilon)^{\tilde O(1/\varepsilon^2)}$, where $\tilde{O}(f(1/\varepsilon))$ hides log factors in $(1/\varepsilon)$ that can depend on the kernel. This implies that by relaxing the notion of boundaries in range queries, eventually the curse of dimensionality disappears, and may help explain the success of machine learning in very high-dimensions. We also complement this result with a lower bound of almost $(1/\varepsilon)^{\Omega(1/\varepsilon)}$, showing the exponential dependence on $1/\varepsilon$ is necessary.

Linear Distance Metric Learning with Noisy Labels

In linear distance metric learning, we are given data in one Euclidean metric space and the goal is to find an appropriate linear map to another Euclidean metric space which respects certain distance conditions as much as possible. In this paper, we formalize a simple and elegant method which reduces to a general continuous convex loss optimization problem, and for different noise models we derive the corresponding loss functions. We show that even if the data is noisy, the ground truth linear metric can be learned with any precision provided access to enough samples, and we provide a corresponding sample complexity bound. Moreover, we present an effective way to truncate the learned model to a low-rank model that can provably maintain the accuracy in loss function and in parameters -- the first such results of this type. Several experimental observations on synthetic and real data sets support and inform our theoretical results.

Mitigating Exploitation Bias in Learning to Rank with an Uncertainty-aware Empirical Bayes Approach

Ranking is at the core of many artificial intelligence (AI) applications, including search engines, recommender systems, etc. Modern ranking systems are often constructed with learning-to-rank (LTR) models built from user behavior signals. While previous studies have demonstrated the effectiveness of using user behavior signals (e.g., clicks) as both features and labels of LTR algorithms, we argue that existing LTR algorithms that indiscriminately treat behavior and non-behavior signals in input features could lead to suboptimal performance in practice. Particularly because user behavior signals often have strong correlations with the ranking objective and can only be collected on items that have already been shown to users, directly using behavior signals in LTR could create an exploitation bias that hurts the system performance in the long run. To address the exploitation bias, we propose EBRank, an empirical Bayes-based uncertainty-aware ranking algorithm. Specifically, to overcome exploitation bias brought by behavior features in ranking models, EBRank uses a sole non-behavior feature based prior model to get a prior estimation of relevance. In the dynamic training and serving of ranking systems, EBRank uses the observed user behaviors to update posterior relevance estimation instead of concatenating behaviors as features in ranking models. Besides, EBRank additionally applies an uncertainty-aware exploration strategy to explore actively, collect user behaviors for empirical Bayesian modeling and improve ranking performance. Experiments on three public datasets show that EBRank is effective, practical and significantly outperforms state-of-the-art ranking algorithms.

Batch Multi-Fidelity Active Learning with Budget Constraints

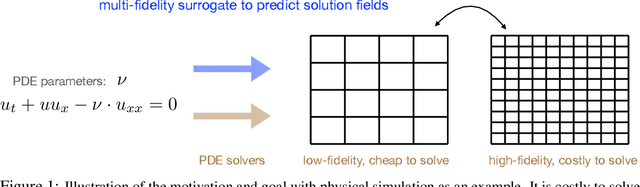
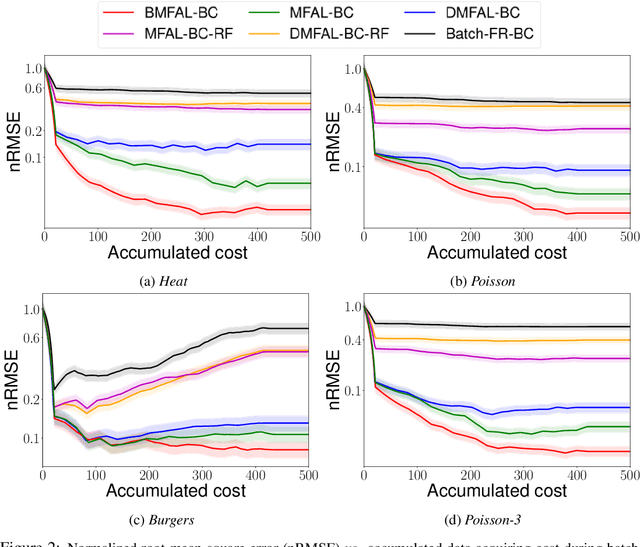
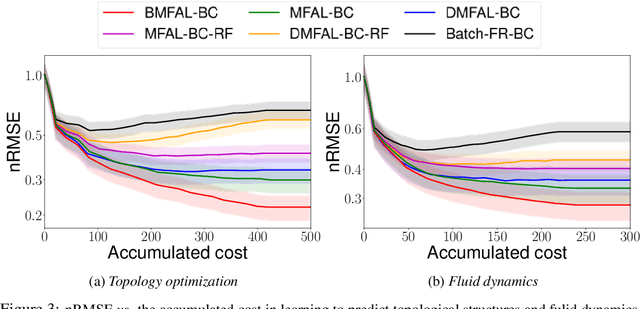
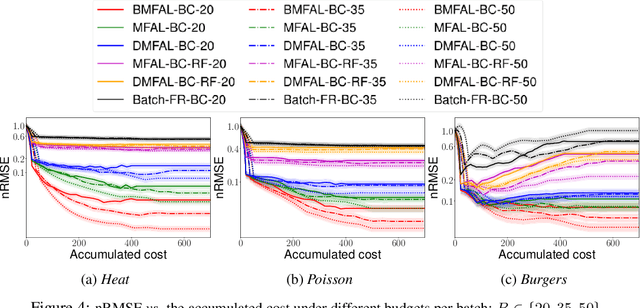
Learning functions with high-dimensional outputs is critical in many applications, such as physical simulation and engineering design. However, collecting training examples for these applications is often costly, e.g. by running numerical solvers. The recent work (Li et al., 2022) proposes the first multi-fidelity active learning approach for high-dimensional outputs, which can acquire examples at different fidelities to reduce the cost while improving the learning performance. However, this method only queries at one pair of fidelity and input at a time, and hence has a risk to bring in strongly correlated examples to reduce the learning efficiency. In this paper, we propose Batch Multi-Fidelity Active Learning with Budget Constraints (BMFAL-BC), which can promote the diversity of training examples to improve the benefit-cost ratio, while respecting a given budget constraint for batch queries. Hence, our method can be more practically useful. Specifically, we propose a novel batch acquisition function that measures the mutual information between a batch of multi-fidelity queries and the target function, so as to penalize highly correlated queries and encourages diversity. The optimization of the batch acquisition function is challenging in that it involves a combinatorial search over many fidelities while subject to the budget constraint. To address this challenge, we develop a weighted greedy algorithm that can sequentially identify each (fidelity, input) pair, while achieving a near $(1 - 1/e)$-approximation of the optimum. We show the advantage of our method in several computational physics and engineering applications.

Classifying Spatial Trajectories

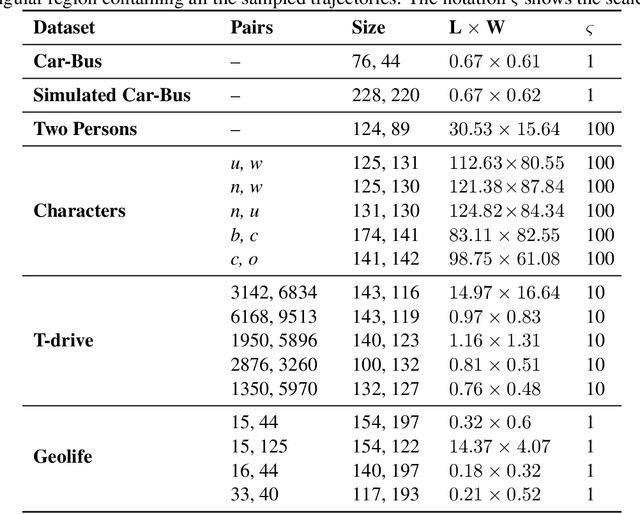
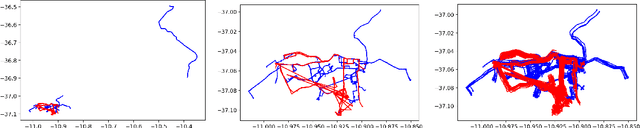
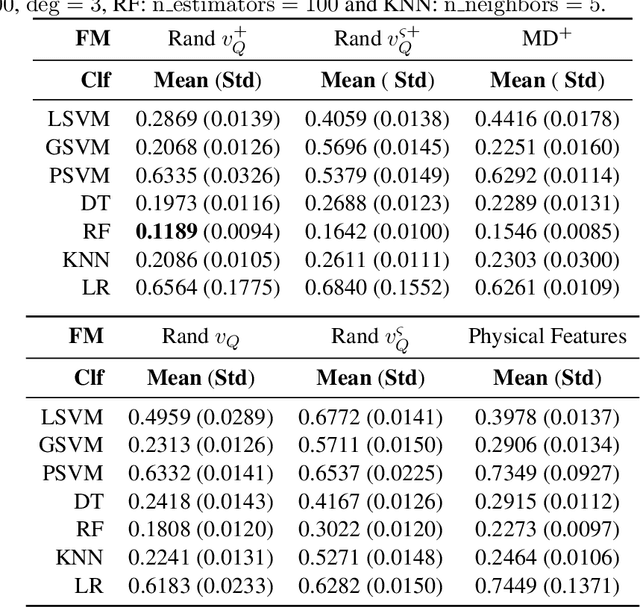
We provide the first comprehensive study on how to classify trajectories using only their spatial representations, measured on 5 real-world data sets. Our comparison considers 20 distinct classifiers arising either as a KNN classifier of a popular distance, or as a more general type of classifier using a vectorized representation of each trajectory. We additionally develop new methods for how to vectorize trajectories via a data-driven method to select the associated landmarks, and these methods prove among the most effective in our study. These vectorized approaches are simple and efficient to use, and also provide state-of-the-art accuracy on an established transportation mode classification task. In all, this study sets the standard for how to classify trajectories, including introducing new simple techniques to achieve these results, and sets a rigorous standard for the inevitable future study on this topic.