Fourier PINNs: From Strong Boundary Conditions to Adaptive Fourier Bases

Interest is rising in Physics-Informed Neural Networks (PINNs) as a mesh-free alternative to traditional numerical solvers for partial differential equations (PDEs). However, PINNs often struggle to learn high-frequency and multi-scale target solutions. To tackle this problem, we first study a strong Boundary Condition (BC) version of PINNs for Dirichlet BCs and observe a consistent decline in relative error compared to the standard PINNs. We then perform a theoretical analysis based on the Fourier transform and convolution theorem. We find that strong BC PINNs can better learn the amplitudes of high-frequency components of the target solutions. However, constructing the architecture for strong BC PINNs is difficult for many BCs and domain geometries. Enlightened by our theoretical analysis, we propose Fourier PINNs -- a simple, general, yet powerful method that augments PINNs with pre-specified, dense Fourier bases. Our proposed architecture likewise learns high-frequency components better but places no restrictions on the particular BCs or problem domains. We develop an adaptive learning and basis selection algorithm via alternating neural net basis optimization, Fourier and neural net basis coefficient estimation, and coefficient truncation. This scheme can flexibly identify the significant frequencies while weakening the nominal frequencies to better capture the target solution's power spectrum. We show the advantage of our approach through a set of systematic experiments.

HyResPINNs: Adaptive Hybrid Residual Networks for Learning Optimal Combinations of Neural and RBF Components for Physics-Informed Modeling

Physics-informed neural networks (PINNs) are an increasingly popular class of techniques for the numerical solution of partial differential equations (PDEs), where neural networks are trained using loss functions regularized by relevant PDE terms to enforce physical constraints. We present a new class of PINNs called HyResPINNs, which augment traditional PINNs with adaptive hybrid residual blocks that combine the outputs of a standard neural network and a radial basis function (RBF) network. A key feature of our method is the inclusion of adaptive combination parameters within each residual block, which dynamically learn to weigh the contributions of the neural network and RBF network outputs. Additionally, adaptive connections between residual blocks allow for flexible information flow throughout the network. We show that HyResPINNs are more robust to training point locations and neural network architectures than traditional PINNs. Moreover, HyResPINNs offer orders of magnitude greater accuracy than competing methods on certain problems, with only modest increases in training costs. We demonstrate the strengths of our approach on challenging PDEs, including the Allen-Cahn equation and the Darcy-Flow equation. Our results suggest that HyResPINNs effectively bridge the gap between traditional numerical methods and modern machine learning-based solvers.

Complexity-Aware Deep Symbolic Regression with Robust Risk-Seeking Policy Gradients

This paper proposes a novel deep symbolic regression approach to enhance the robustness and interpretability of data-driven mathematical expression discovery. Despite the success of the state-of-the-art method, DSR, it is built on recurrent neural networks, purely guided by data fitness, and potentially meet tail barriers, which can zero out the policy gradient and cause inefficient model updates. To overcome these limitations, we use transformers in conjunction with breadth-first-search to improve the learning performance. We use Bayesian information criterion (BIC) as the reward function to explicitly account for the expression complexity and optimize the trade-off between interpretability and data fitness. We propose a modified risk-seeking policy that not only ensures the unbiasness of the gradient, but also removes the tail barriers, thus ensuring effective updates from top performers. Through a series of benchmarks and systematic experiments, we demonstrate the advantages of our approach.

Polynomial-Augmented Neural Networks (PANNs) with Weak Orthogonality Constraints for Enhanced Function and PDE Approximation

We present polynomial-augmented neural networks (PANNs), a novel machine learning architecture that combines deep neural networks (DNNs) with a polynomial approximant. PANNs combine the strengths of DNNs (flexibility and efficiency in higher-dimensional approximation) with those of polynomial approximation (rapid convergence rates for smooth functions). To aid in both stable training and enhanced accuracy over a variety of problems, we present (1) a family of orthogonality constraints that impose mutual orthogonality between the polynomial and the DNN within a PANN; (2) a simple basis pruning approach to combat the curse of dimensionality introduced by the polynomial component; and (3) an adaptation of a polynomial preconditioning strategy to both DNNs and polynomials. We test the resulting architecture for its polynomial reproduction properties, ability to approximate both smooth functions and functions of limited smoothness, and as a method for the solution of partial differential equations (PDEs). Through these experiments, we demonstrate that PANNs offer superior approximation properties to DNNs for both regression and the numerical solution of PDEs, while also offering enhanced accuracy over both polynomial and DNN-based regression (each) when regressing functions with limited smoothness.

Kolmogorov n-Widths for Multitask Physics-Informed Machine Learning (PIML) Methods: Towards Robust Metrics

Physics-informed machine learning (PIML) as a means of solving partial differential equations (PDE) has garnered much attention in the Computational Science and Engineering (CS&E) world. This topic encompasses a broad array of methods and models aimed at solving a single or a collection of PDE problems, called multitask learning. PIML is characterized by the incorporation of physical laws into the training process of machine learning models in lieu of large data when solving PDE problems. Despite the overall success of this collection of methods, it remains incredibly difficult to analyze, benchmark, and generally compare one approach to another. Using Kolmogorov n-widths as a measure of effectiveness of approximating functions, we judiciously apply this metric in the comparison of various multitask PIML architectures. We compute lower accuracy bounds and analyze the model's learned basis functions on various PDE problems. This is the first objective metric for comparing multitask PIML architectures and helps remove uncertainty in model validation from selective sampling and overfitting. We also identify avenues of improvement for model architectures, such as the choice of activation function, which can drastically affect model generalization to "worst-case" scenarios, which is not observed when reporting task-specific errors. We also incorporate this metric into the optimization process through regularization, which improves the models' generalizability over the multitask PDE problem.

Equation Discovery with Bayesian Spike-and-Slab Priors and Efficient Kernels

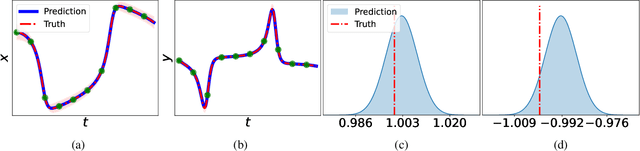
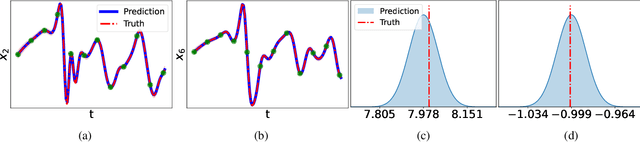
Discovering governing equations from data is important to many scientific and engineering applications. Despite promising successes, existing methods are still challenged by data sparsity as well as noise issues, both of which are ubiquitous in practice. Moreover, state-of-the-art methods lack uncertainty quantification and/or are costly in training. To overcome these limitations, we propose a novel equation discovery method based on Kernel learning and BAyesian Spike-and-Slab priors (KBASS). We use kernel regression to estimate the target function, which is flexible, expressive, and more robust to data sparsity and noises. We combine it with a Bayesian spike-and-slab prior -- an ideal Bayesian sparse distribution -- for effective operator selection and uncertainty quantification. We develop an expectation propagation expectation-maximization (EP-EM) algorithm for efficient posterior inference and function estimation. To overcome the computational challenge of kernel regression, we place the function values on a mesh and induce a Kronecker product construction, and we use tensor algebra methods to enable efficient computation and optimization. We show the significant advantages of KBASS on a list of benchmark ODE and PDE discovery tasks.

Neural Operator Learning for Ultrasound Tomography Inversion

Neural operator learning as a means of mapping between complex function spaces has garnered significant attention in the field of computational science and engineering (CS&E). In this paper, we apply Neural operator learning to the time-of-flight ultrasound computed tomography (USCT) problem. We learn the mapping between time-of-flight (TOF) data and the heterogeneous sound speed field using a full-wave solver to generate the training data. This novel application of operator learning circumnavigates the need to solve the computationally intensive iterative inverse problem. The operator learns the non-linear mapping offline and predicts the heterogeneous sound field with a single forward pass through the model. This is the first time operator learning has been used for ultrasound tomography and is the first step in potential real-time predictions of soft tissue distribution for tumor identification in beast imaging.

A unified scalable framework for causal sweeping strategies for Physics-Informed Neural Networks (PINNs) and their temporal decompositions

Physics-informed neural networks (PINNs) as a means of solving partial differential equations (PDE) have garnered much attention in Computational Science and Engineering (CS&E). However, a recent topic of interest is exploring various training (i.e., optimization) challenges - in particular, arriving at poor local minima in the optimization landscape results in a PINN approximation giving an inferior, and sometimes trivial, solution when solving forward time-dependent PDEs with no data. This problem is also found in, and in some sense more difficult, with domain decomposition strategies such as temporal decomposition using XPINNs. To address this problem, we first enable a general categorization for previous causality methods, from which we identify a gap in the previous approaches. We then furnish examples and explanations for different training challenges, their cause, and how they relate to information propagation and temporal decomposition. We propose a solution to fill this gap by reframing these causality concepts into a generalized information propagation framework in which any prior method or combination of methods can be described. Our unified framework moves toward reducing the number of PINN methods to consider and the implementation and retuning cost for thorough comparisons. We propose a new stacked-decomposition method that bridges the gap between time-marching PINNs and XPINNs. We also introduce significant computational speed-ups by using transfer learning concepts to initialize subnetworks in the domain and loss tolerance-based propagation for the subdomains. We formulate a new time-sweeping collocation point algorithm inspired by the previous PINNs causality literature, which our framework can still describe, and provides a significant computational speed-up via reduced-cost collocation point segmentation. Finally, we provide numerical results on baseline PDE problems.

Deep neural operators can serve as accurate surrogates for shape optimization: A case study for airfoils

Deep neural operators, such as DeepONets, have changed the paradigm in high-dimensional nonlinear regression from function regression to (differential) operator regression, paving the way for significant changes in computational engineering applications. Here, we investigate the use of DeepONets to infer flow fields around unseen airfoils with the aim of shape optimization, an important design problem in aerodynamics that typically taxes computational resources heavily. We present results which display little to no degradation in prediction accuracy, while reducing the online optimization cost by orders of magnitude. We consider NACA airfoils as a test case for our proposed approach, as their shape can be easily defined by the four-digit parametrization. We successfully optimize the constrained NACA four-digit problem with respect to maximizing the lift-to-drag ratio and validate all results by comparing them to a high-order CFD solver. We find that DeepONets have low generalization error, making them ideal for generating solutions of unseen shapes. Specifically, pressure, density, and velocity fields are accurately inferred at a fraction of a second, hence enabling the use of general objective functions beyond the maximization of the lift-to-drag ratio considered in the current work.

Batch Multi-Fidelity Active Learning with Budget Constraints

Learning functions with high-dimensional outputs is critical in many applications, such as physical simulation and engineering design. However, collecting training examples for these applications is often costly, e.g. by running numerical solvers. The recent work (Li et al., 2022) proposes the first multi-fidelity active learning approach for high-dimensional outputs, which can acquire examples at different fidelities to reduce the cost while improving the learning performance. However, this method only queries at one pair of fidelity and input at a time, and hence has a risk to bring in strongly correlated examples to reduce the learning efficiency. In this paper, we propose Batch Multi-Fidelity Active Learning with Budget Constraints (BMFAL-BC), which can promote the diversity of training examples to improve the benefit-cost ratio, while respecting a given budget constraint for batch queries. Hence, our method can be more practically useful. Specifically, we propose a novel batch acquisition function that measures the mutual information between a batch of multi-fidelity queries and the target function, so as to penalize highly correlated queries and encourages diversity. The optimization of the batch acquisition function is challenging in that it involves a combinatorial search over many fidelities while subject to the budget constraint. To address this challenge, we develop a weighted greedy algorithm that can sequentially identify each (fidelity, input) pair, while achieving a near $(1 - 1/e)$-approximation of the optimum. We show the advantage of our method in several computational physics and engineering applications.