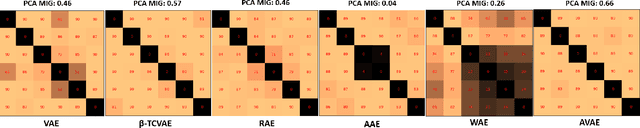
Disentanglement Analysis in Deep Latent Variable Models Matching Aggregate Posterior Distributions

Deep latent variable models (DLVMs) are designed to learn meaningful representations in an unsupervised manner, such that the hidden explanatory factors are interpretable by independent latent variables (aka disentanglement). The variational autoencoder (VAE) is a popular DLVM widely studied in disentanglement analysis due to the modeling of the posterior distribution using a factorized Gaussian distribution that encourages the alignment of the latent factors with the latent axes. Several metrics have been proposed recently, assuming that the latent variables explaining the variation in data are aligned with the latent axes (cardinal directions). However, there are other DLVMs, such as the AAE and WAE-MMD (matching the aggregate posterior to the prior), where the latent variables might not be aligned with the latent axes. In this work, we propose a statistical method to evaluate disentanglement for any DLVMs in general. The proposed technique discovers the latent vectors representing the generative factors of a dataset that can be different from the cardinal latent axes. We empirically demonstrate the advantage of the method on two datasets.

ARD-VAE: A Statistical Formulation to Find the Relevant Latent Dimensions of Variational Autoencoders

The variational autoencoder (VAE) is a popular, deep, latent-variable model (DLVM) due to its simple yet effective formulation for modeling the data distribution. Moreover, optimizing the VAE objective function is more manageable than other DLVMs. The bottleneck dimension of the VAE is a crucial design choice, and it has strong ramifications for the model's performance, such as finding the hidden explanatory factors of a dataset using the representations learned by the VAE. However, the size of the latent dimension of the VAE is often treated as a hyperparameter estimated empirically through trial and error. To this end, we propose a statistical formulation to discover the relevant latent factors required for modeling a dataset. In this work, we use a hierarchical prior in the latent space that estimates the variance of the latent axes using the encoded data, which identifies the relevant latent dimensions. For this, we replace the fixed prior in the VAE objective function with a hierarchical prior, keeping the remainder of the formulation unchanged. We call the proposed method the automatic relevancy detection in the variational autoencoder (ARD-VAE). We demonstrate the efficacy of the ARD-VAE on multiple benchmark datasets in finding the relevant latent dimensions and their effect on different evaluation metrics, such as FID score and disentanglement analysis.

The Silent Majority: Demystifying Memorization Effect in the Presence of Spurious Correlations

Machine learning models often rely on simple spurious features -- patterns in training data that correlate with targets but are not causally related to them, like image backgrounds in foreground classification. This reliance typically leads to imbalanced test performance across minority and majority groups. In this work, we take a closer look at the fundamental cause of such imbalanced performance through the lens of memorization, which refers to the ability to predict accurately on \textit{atypical} examples (minority groups) in the training set but failing in achieving the same accuracy in the testing set. This paper systematically shows the ubiquitous existence of spurious features in a small set of neurons within the network, providing the first-ever evidence that memorization may contribute to imbalanced group performance. Through three experimental sources of converging empirical evidence, we find the property of a small subset of neurons or channels in memorizing minority group information. Inspired by these findings, we articulate the hypothesis: the imbalanced group performance is a byproduct of ``noisy'' spurious memorization confined to a small set of neurons. To further substantiate this hypothesis, we show that eliminating these unnecessary spurious memorization patterns via a novel framework during training can significantly affect the model performance on minority groups. Our experimental results across various architectures and benchmarks offer new insights on how neural networks encode core and spurious knowledge, laying the groundwork for future research in demystifying robustness to spurious correlation.

LEDA: Log-Euclidean Diffeomorphic Autoencoder for Efficient Statistical Analysis of Diffeomorphism

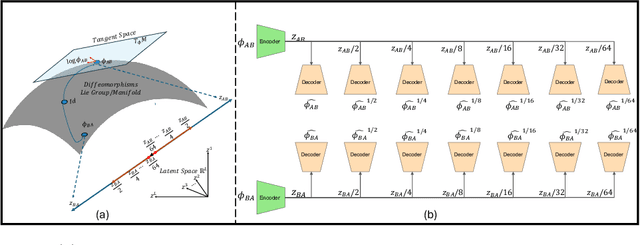
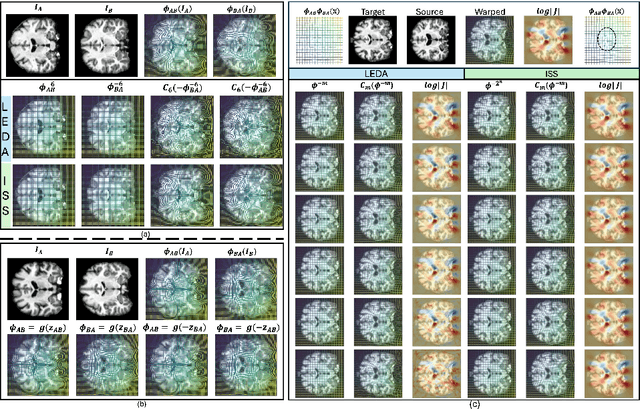
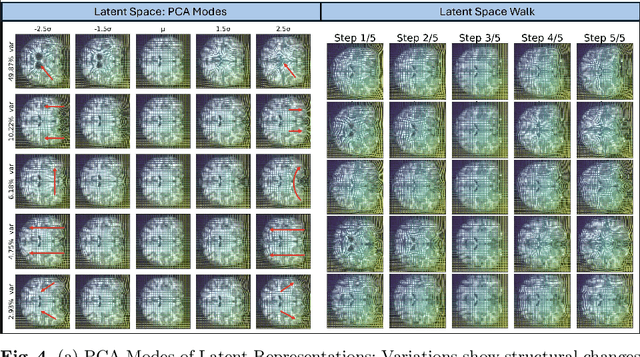
Image registration is a core task in computational anatomy that establishes correspondences between images. Invertible deformable registration, which computes a deformation field and handles complex, non-linear transformation, is essential for tracking anatomical variations, especially in neuroimaging applications where inter-subject differences and longitudinal changes are key. Analyzing the deformation fields is challenging due to their non-linearity, limiting statistical analysis. However, traditional approaches for analyzing deformation fields are computationally expensive, sensitive to initialization, and prone to numerical errors, especially when the deformation is far from the identity. To address these limitations, we propose the Log-Euclidean Diffeomorphic Autoencoder (LEDA), an innovative framework designed to compute the principal logarithm of deformation fields by efficiently predicting consecutive square roots. LEDA operates within a linearized latent space that adheres to the diffeomorphisms group action laws, enhancing our model's robustness and applicability. We also introduce a loss function to enforce inverse consistency, ensuring accurate latent representations of deformation fields. Extensive experiments with the OASIS-1 dataset demonstrate the effectiveness of LEDA in accurately modeling and analyzing complex non-linear deformations while maintaining inverse consistency. Additionally, we evaluate its ability to capture and incorporate clinical variables, enhancing its relevance for clinical applications.

Refining Skewed Perceptions in Vision-Language Models through Visual Representations

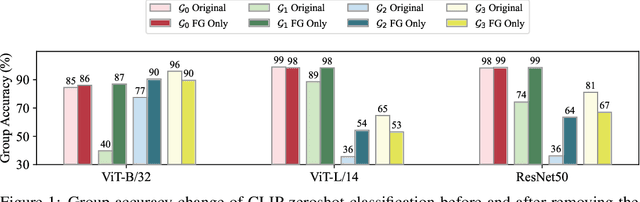
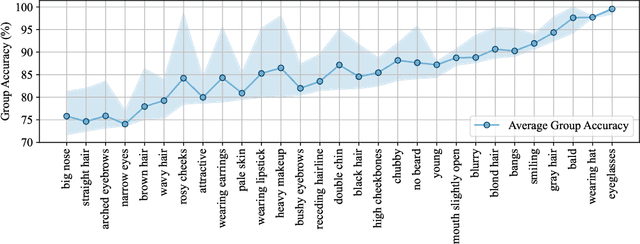
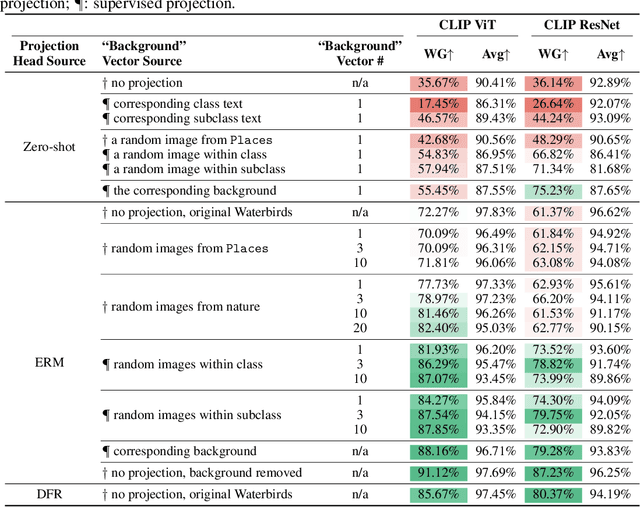
Large vision-language models (VLMs), such as CLIP, have become foundational, demonstrating remarkable success across a variety of downstream tasks. Despite their advantages, these models, akin to other foundational systems, inherit biases from the disproportionate distribution of real-world data, leading to misconceptions about the actual environment. Prevalent datasets like ImageNet are often riddled with non-causal, spurious correlations that can diminish VLM performance in scenarios where these contextual elements are absent. This study presents an investigation into how a simple linear probe can effectively distill task-specific core features from CLIP's embedding for downstream applications. Our analysis reveals that the CLIP text representations are often tainted by spurious correlations, inherited in the biased pre-training dataset. Empirical evidence suggests that relying on visual representations from CLIP, as opposed to text embedding, is more practical to refine the skewed perceptions in VLMs, emphasizing the superior utility of visual representations in overcoming embedded biases. Our codes will be available here.

Matching aggregate posteriors in the variational autoencoder

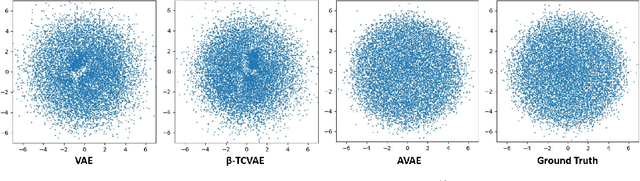
The variational autoencoder (VAE) is a well-studied, deep, latent-variable model (DLVM) that efficiently optimizes the variational lower bound of the log marginal data likelihood and has a strong theoretical foundation. However, the VAE's known failure to match the aggregate posterior often results in \emph{pockets/holes} in the latent distribution (i.e., a failure to match the prior) and/or \emph{posterior collapse}, which is associated with a loss of information in the latent space. This paper addresses these shortcomings in VAEs by reformulating the objective function associated with VAEs in order to match the aggregate/marginal posterior distribution to the prior. We use kernel density estimate (KDE) to model the aggregate posterior in high dimensions. The proposed method is named the \emph{aggregate variational autoencoder} (AVAE) and is built on the theoretical framework of the VAE. Empirical evaluation of the proposed method on multiple benchmark data sets demonstrates the effectiveness of the AVAE relative to state-of-the-art (SOTA) methods.

Analyzing the Domain Shift Immunity of Deep Homography Estimation

Homography estimation is a basic image-alignment method in many applications. Recently, with the development of convolutional neural networks (CNNs), some learning based approaches have shown great success in this task. However, the performance across different domains has never been researched. Unlike other common tasks (\eg, classification, detection, segmentation), CNN based homography estimation models show a domain shift immunity, which means a model can be trained on one dataset and tested on another without any transfer learning. To explain this unusual performance, we need to determine how CNNs estimate homography. In this study, we first show the domain shift immunity of different deep homography estimation models. We then use a shallow network with a specially designed dataset to analyze the features used for estimation. The results show that networks use low-level texture information to estimate homography. We also design some experiments to compare the performance between different texture densities and image features distorted on some common datasets to demonstrate our findings. Based on these findings, we provide an explanation of the domain shift immunity of deep homography estimation.

Neural Operator Learning for Ultrasound Tomography Inversion

Neural operator learning as a means of mapping between complex function spaces has garnered significant attention in the field of computational science and engineering (CS&E). In this paper, we apply Neural operator learning to the time-of-flight ultrasound computed tomography (USCT) problem. We learn the mapping between time-of-flight (TOF) data and the heterogeneous sound speed field using a full-wave solver to generate the training data. This novel application of operator learning circumnavigates the need to solve the computationally intensive iterative inverse problem. The operator learns the non-linear mapping offline and predicts the heterogeneous sound field with a single forward pass through the model. This is the first time operator learning has been used for ultrasound tomography and is the first step in potential real-time predictions of soft tissue distribution for tumor identification in beast imaging.

Physics Informed Convex Artificial Neural Networks (PICANNs) for Optimal Transport based Density Estimation

Optimal Mass Transport (OMT) is a well studied problem with a variety of applications in a diverse set of fields ranging from Physics to Computer Vision and in particular Statistics and Data Science. Since the original formulation of Monge in 1781 significant theoretical progress been made on the existence, uniqueness and properties of the optimal transport maps. The actual numerical computation of the transport maps, particularly in high dimensions, remains a challenging problem. By Brenier's theorem, the continuous OMT problem can be reduced to that of solving a non-linear PDE of Monge-Ampere type whose solution is a convex function. In this paper, building on recent developments of input convex neural networks and physics informed neural networks for solving PDE's, we propose a Deep Learning approach to solve the continuous OMT problem. To demonstrate the versatility of our framework we focus on the ubiquitous density estimation and generative modeling tasks in statistics and machine learning. Finally as an example we show how our framework can be incorporated with an autoencoder to estimate an effective probabilistic generative model.

Learning Multiparametric Biomarkers for Assessing MR-Guided Focused Ultrasound Treatments Using Volume-Conserving Registration

Noninvasive MR-guided focused ultrasound (MRgFUS) treatments are promising alternatives to the surgical removal of malignant tumors. A significant challenge is assessing the treated tissue immediately after MRgFUS procedures. Although current clinical assessment uses the immediate nonperfused volume (NPV) biomarker derived from contrast enhanced imaging, the use of contrast agent prevents continuing MRgFUS treatment if margins are not adequate. In addition, the NPV has been shown to provide variable accuracy for the true treatment outcome as evaluated by follow-up biomarkers. This work presents a novel, noncontrast, learned multiparametric MR biomarker that is conducive for intratreatment assessment. MRgFUS ablations were performed in a rabbit VX2 tumor model. Multiparametric MRI was obtained both during and immediately after the MRgFUS ablation, as well as during follow-up imaging. Segmentation of the NPV obtained during follow-up imaging was used to train a neural network on noncontrast multiparametric MR images. The NPV follow-up segmentation was registered to treatment-day images using a novel volume-conserving registration algorithm, allowing a voxel-wise correlation between imaging sessions. Contrasted with state-of-the-art registration algorithms that change the average volume by 16.8%, the presented volume-conserving registration algorithm changes the average volume by only 0.28%. After registration, the learned multiparametric MR biomarker predicted the follow-up NPV with an average DICE coefficient of 0.71, outperforming the DICE coefficient of 0.53 from the current standard of NPV obtained immediately after the ablation treatment. Noncontrast multiparametric MR imaging can provide a more accurate prediction of treated tissue immediately after treatment. Noncontrast assessment of MRgFUS procedures will potentially lead to more efficacious MRgFUS ablation treatments.