The Silent Majority: Demystifying Memorization Effect in the Presence of Spurious Correlations

Machine learning models often rely on simple spurious features -- patterns in training data that correlate with targets but are not causally related to them, like image backgrounds in foreground classification. This reliance typically leads to imbalanced test performance across minority and majority groups. In this work, we take a closer look at the fundamental cause of such imbalanced performance through the lens of memorization, which refers to the ability to predict accurately on \textit{atypical} examples (minority groups) in the training set but failing in achieving the same accuracy in the testing set. This paper systematically shows the ubiquitous existence of spurious features in a small set of neurons within the network, providing the first-ever evidence that memorization may contribute to imbalanced group performance. Through three experimental sources of converging empirical evidence, we find the property of a small subset of neurons or channels in memorizing minority group information. Inspired by these findings, we articulate the hypothesis: the imbalanced group performance is a byproduct of ``noisy'' spurious memorization confined to a small set of neurons. To further substantiate this hypothesis, we show that eliminating these unnecessary spurious memorization patterns via a novel framework during training can significantly affect the model performance on minority groups. Our experimental results across various architectures and benchmarks offer new insights on how neural networks encode core and spurious knowledge, laying the groundwork for future research in demystifying robustness to spurious correlation.

Refining Skewed Perceptions in Vision-Language Models through Visual Representations

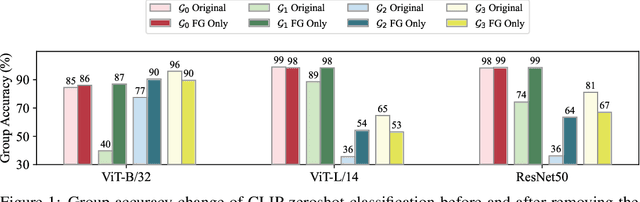
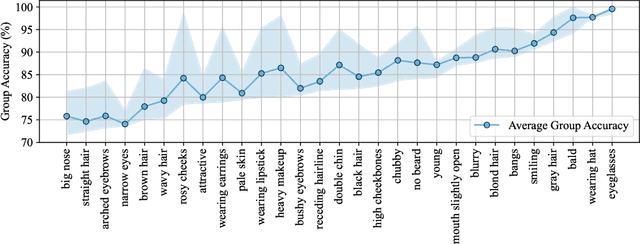
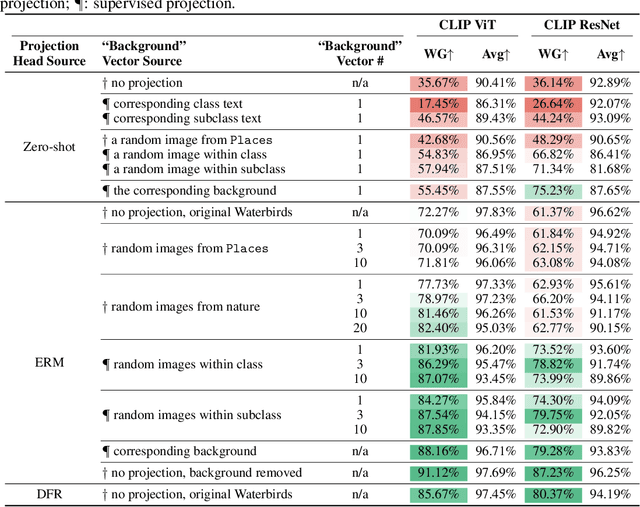
Large vision-language models (VLMs), such as CLIP, have become foundational, demonstrating remarkable success across a variety of downstream tasks. Despite their advantages, these models, akin to other foundational systems, inherit biases from the disproportionate distribution of real-world data, leading to misconceptions about the actual environment. Prevalent datasets like ImageNet are often riddled with non-causal, spurious correlations that can diminish VLM performance in scenarios where these contextual elements are absent. This study presents an investigation into how a simple linear probe can effectively distill task-specific core features from CLIP's embedding for downstream applications. Our analysis reveals that the CLIP text representations are often tainted by spurious correlations, inherited in the biased pre-training dataset. Empirical evidence suggests that relying on visual representations from CLIP, as opposed to text embedding, is more practical to refine the skewed perceptions in VLMs, emphasizing the superior utility of visual representations in overcoming embedded biases. Our codes will be available here.

Neural Operator Learning for Ultrasound Tomography Inversion

Neural operator learning as a means of mapping between complex function spaces has garnered significant attention in the field of computational science and engineering (CS&E). In this paper, we apply Neural operator learning to the time-of-flight ultrasound computed tomography (USCT) problem. We learn the mapping between time-of-flight (TOF) data and the heterogeneous sound speed field using a full-wave solver to generate the training data. This novel application of operator learning circumnavigates the need to solve the computationally intensive iterative inverse problem. The operator learns the non-linear mapping offline and predicts the heterogeneous sound field with a single forward pass through the model. This is the first time operator learning has been used for ultrasound tomography and is the first step in potential real-time predictions of soft tissue distribution for tumor identification in beast imaging.

Deep Learning the Shape of the Brain Connectome

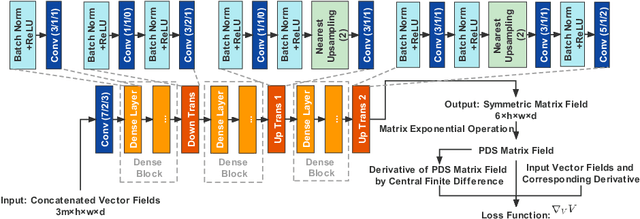
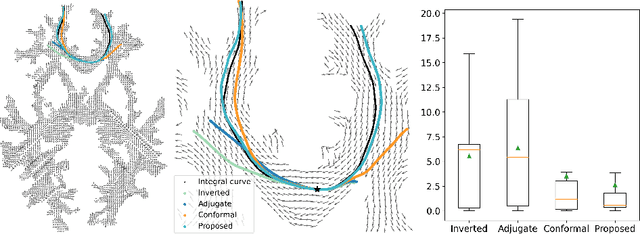
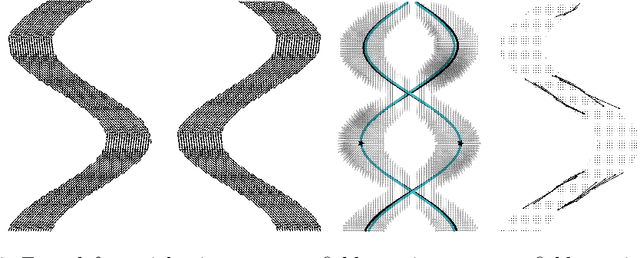
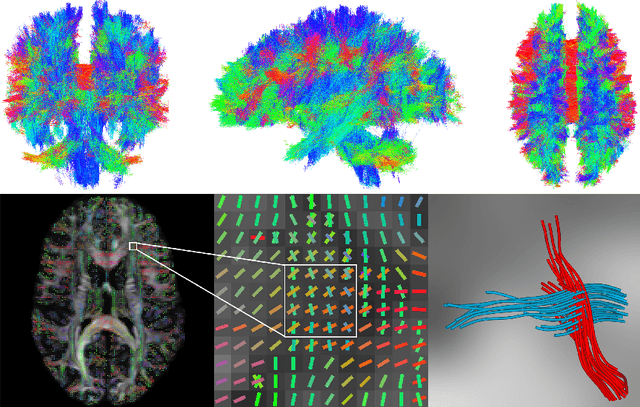
To statistically study the variability and differences between normal and abnormal brain connectomes, a mathematical model of the neural connections is required. In this paper, we represent the brain connectome as a Riemannian manifold, which allows us to model neural connections as geodesics. We show for the first time how one can leverage deep neural networks to estimate a Riemannian metric of the brain that can accommodate fiber crossings and is a natural modeling tool to infer the shape of the brain from DWMRI. Our method achieves excellent performance in geodesic-white-matter-pathway alignment and tackles the long-standing issue in previous methods: the inability to recover the crossing fibers with high fidelity.

Integrated Construction of Multimodal Atlases with Structural Connectomes in the Space of Riemannian Metrics

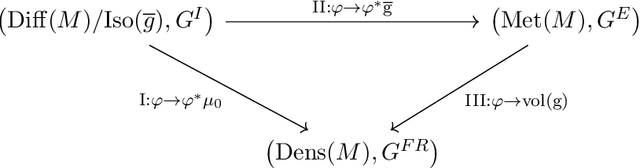
The structural network of the brain, or structural connectome, can be represented by fiber bundles generated by a variety of tractography methods. While such methods give qualitative insights into brain structure, there is controversy over whether they can provide quantitative information, especially at the population level. In order to enable population-level statistical analysis of the structural connectome, we propose representing a connectome as a Riemannian metric, which is a point on an infinite-dimensional manifold. We equip this manifold with the Ebin metric, a natural metric structure for this space, to get a Riemannian manifold along with its associated geometric properties. We then use this Riemannian framework to apply object-oriented statistical analysis to define an atlas as the Fr\'echet mean of a population of Riemannian metrics. This formulation ties into the existing framework for diffeomorphic construction of image atlases, allowing us to construct a multimodal atlas by simultaneously integrating complementary white matter structure details from DWMRI and cortical details from T1-weighted MRI. We illustrate our framework with 2D data examples of connectome registration and atlas formation. Finally, we build an example 3D multimodal atlas using T1 images and connectomes derived from diffusion tensors estimated from a subset of subjects from the Human Connectome Project.

Structural Connectome Atlas Construction in the Space of Riemannian Metrics

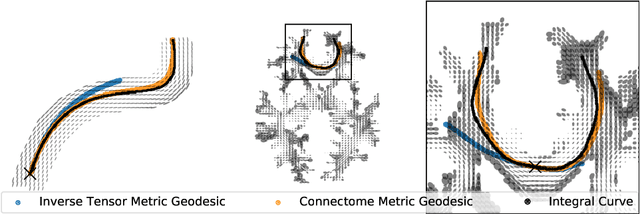
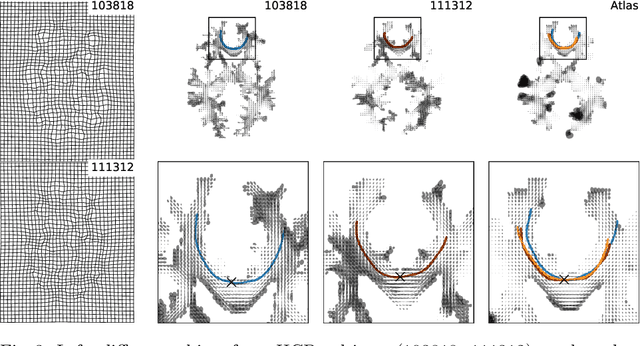
The structural connectome is often represented by fiber bundles generated from various types of tractography. We propose a method of analyzing connectomes by representing them as a Riemannian metric, thereby viewing them as points in an infinite-dimensional manifold. After equipping this space with a natural metric structure, the Ebin metric, we apply object-oriented statistical analysis to define an atlas as the Fr\'echet mean of a population of Riemannian metrics. We demonstrate connectome registration and atlas formation using connectomes derived from diffusion tensors estimated from a subset of subjects from the Human Connectome Project.