Self Supervised Networks for Learning Latent Space Representations of Human Body Scans and Motions

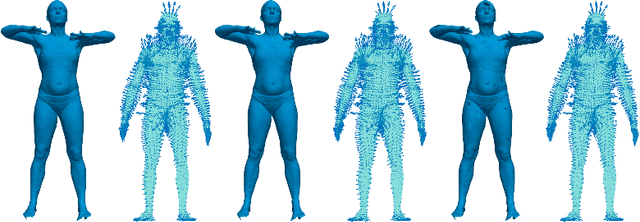
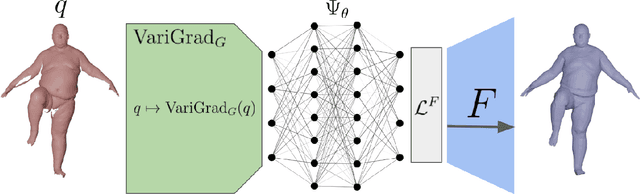
This paper introduces self-supervised neural network models to tackle several fundamental problems in the field of 3D human body analysis and processing. First, we propose VariShaPE (Varifold Shape Parameter Estimator), a novel architecture for the retrieval of latent space representations of body shapes and poses. This network offers a fast and robust method to estimate the embedding of arbitrary unregistered meshes into the latent space. Second, we complement the estimation of latent codes with MoGeN (Motion Geometry Network) a framework that learns the geometry on the latent space itself. This is achieved by lifting the body pose parameter space into a higher dimensional Euclidean space in which body motion mini-sequences from a training set of 4D data can be approximated by simple linear interpolation. Using the SMPL latent space representation we illustrate how the combination of these network models, once trained, can be used to perform a variety of tasks with very limited computational cost. This includes operations such as motion interpolation, extrapolation and transfer as well as random shape and pose generation.

The Z-Gromov-Wasserstein Distance

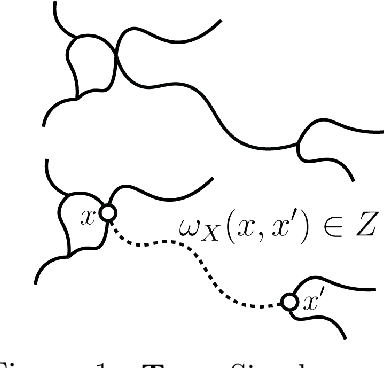
The Gromov-Wasserstein (GW) distance is a powerful tool for comparing metric measure spaces which has found broad applications in data science and machine learning. Driven by the need to analyze datasets whose objects have increasingly complex structure (such as node and edge-attributed graphs), several variants of GW distance have been introduced in the recent literature. With a view toward establishing a general framework for the theory of GW-like distances, this paper considers a vast generalization of the notion of a metric measure space: for an arbitrary metric space $Z$, we define a $Z$-network to be a measure space endowed with a kernel valued in $Z$. We introduce a method for comparing $Z$-networks by defining a generalization of GW distance, which we refer to as $Z$-Gromov-Wasserstein ($Z$-GW) distance. This construction subsumes many previously known metrics and offers a unified approach to understanding their shared properties. The paper demonstrates that the $Z$-GW distance defines a metric on the space of $Z$-networks which retains desirable properties of $Z$, such as separability, completeness, and geodesicity. Many of these properties were unknown for existing variants of GW distance that fall under our framework. Our focus is on foundational theory, but our results also include computable lower bounds and approximations of the distance which will be useful for practical applications.

Basis restricted elastic shape analysis on the space of unregistered surfaces

This paper introduces a new mathematical and numerical framework for surface analysis derived from the general setting of elastic Riemannian metrics on shape spaces. Traditionally, those metrics are defined over the infinite dimensional manifold of immersed surfaces and satisfy specific invariance properties enabling the comparison of surfaces modulo shape preserving transformations such as reparametrizations. The specificity of the approach we develop is to restrict the space of allowable transformations to predefined finite dimensional bases of deformation fields. These are estimated in a data-driven way so as to emulate specific types of surface transformations observed in a training set. The use of such bases allows to simplify the representation of the corresponding shape space to a finite dimensional latent space. However, in sharp contrast with methods involving e.g. mesh autoencoders, the latent space is here equipped with a non-Euclidean Riemannian metric precisely inherited from the family of aforementioned elastic metrics. We demonstrate how this basis restricted model can be then effectively implemented to perform a variety of tasks on surface meshes which, importantly, does not assume these to be pre-registered (i.e. with given point correspondences) or to even have a consistent mesh structure. We specifically validate our approach on human body shape and pose data as well as human face scans, and show how it generally outperforms state-of-the-art methods on problems such as shape registration, interpolation, motion transfer or random pose generation.

BaRe-ESA: A Riemannian Framework for Unregistered Human Body Shapes

We present BaRe-ESA, a novel Riemannian framework for human body scan representation, interpolation and extrapolation. BaRe-ESA operates directly on unregistered meshes, i.e., without the need to establish prior point to point correspondences or to assume a consistent mesh structure. Our method relies on a latent space representation, which is equipped with a Riemannian (non-Euclidean) metric associated to an invariant higher-order metric on the space of surfaces. Experimental results on the FAUST and DFAUST datasets show that BaRe-ESA brings significant improvements with respect to previous solutions in terms of shape registration, interpolation and extrapolation. The efficiency and strength of our model is further demonstrated in applications such as motion transfer and random generation of body shape and pose.

Elastic shape analysis of surfaces with second-order Sobolev metrics: a comprehensive numerical framework

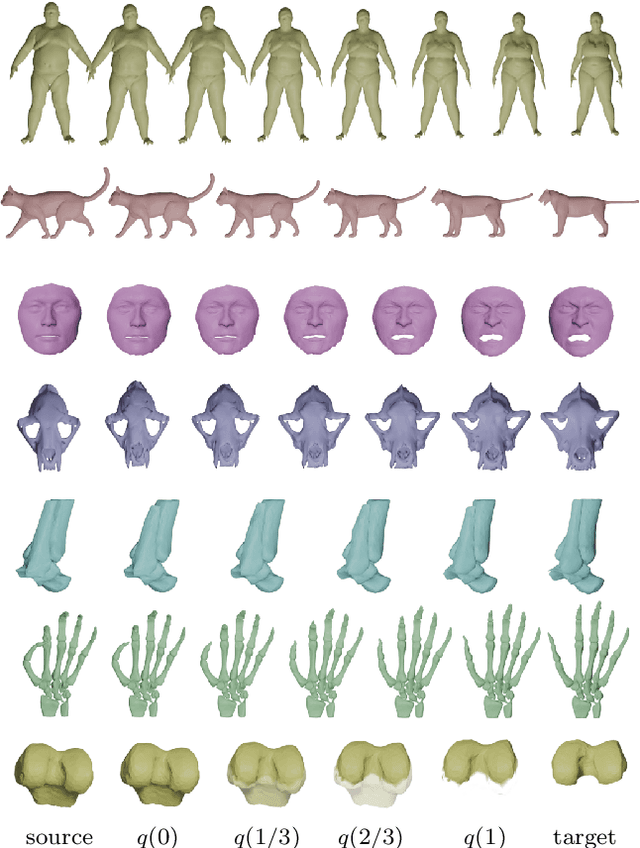
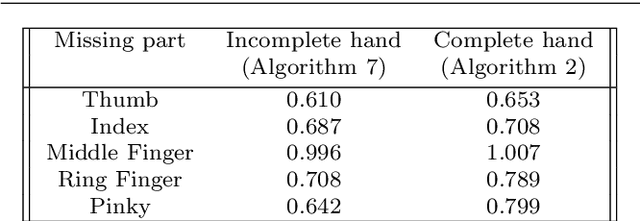
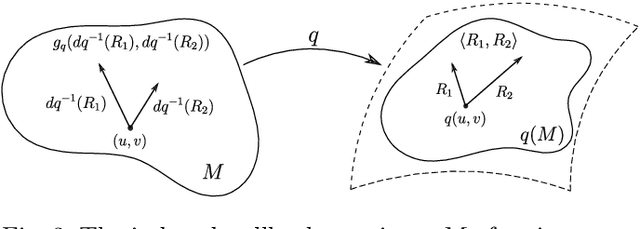
This paper introduces a set of numerical methods for Riemannian shape analysis of 3D surfaces within the setting of invariant (elastic) second-order Sobolev metrics. More specifically, we address the computation of geodesics and geodesic distances between parametrized or unparametrized immersed surfaces represented as 3D meshes. Building on this, we develop tools for the statistical shape analysis of sets of surfaces, including methods for estimating Karcher means and performing tangent PCA on shape populations, and for computing parallel transport along paths of surfaces. Our proposed approach fundamentally relies on a relaxed variational formulation for the geodesic matching problem via the use of varifold fidelity terms, which enable us to enforce reparametrization independence when computing geodesics between unparametrized surfaces, while also yielding versatile algorithms that allow us to compare surfaces with varying sampling or mesh structures. Importantly, we demonstrate how our relaxed variational framework can be extended to tackle partially observed data. The different benefits of our numerical pipeline are illustrated over various examples, synthetic and real.

Deep Learning the Shape of the Brain Connectome

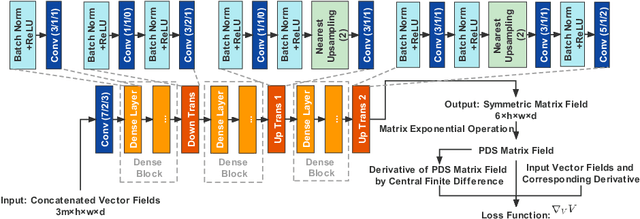
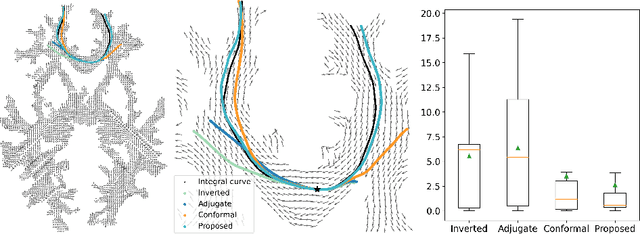
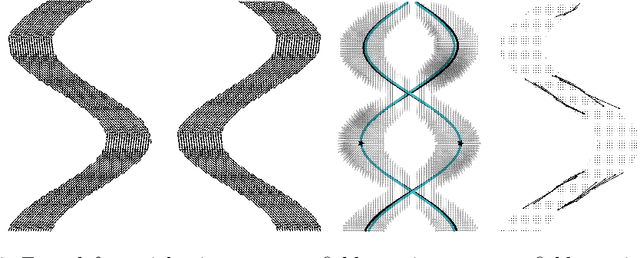
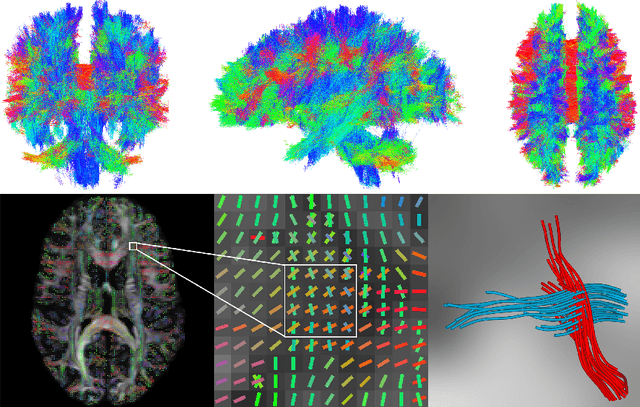
To statistically study the variability and differences between normal and abnormal brain connectomes, a mathematical model of the neural connections is required. In this paper, we represent the brain connectome as a Riemannian manifold, which allows us to model neural connections as geodesics. We show for the first time how one can leverage deep neural networks to estimate a Riemannian metric of the brain that can accommodate fiber crossings and is a natural modeling tool to infer the shape of the brain from DWMRI. Our method achieves excellent performance in geodesic-white-matter-pathway alignment and tackles the long-standing issue in previous methods: the inability to recover the crossing fibers with high fidelity.

Integrated Construction of Multimodal Atlases with Structural Connectomes in the Space of Riemannian Metrics

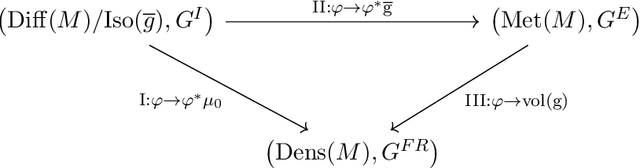
The structural network of the brain, or structural connectome, can be represented by fiber bundles generated by a variety of tractography methods. While such methods give qualitative insights into brain structure, there is controversy over whether they can provide quantitative information, especially at the population level. In order to enable population-level statistical analysis of the structural connectome, we propose representing a connectome as a Riemannian metric, which is a point on an infinite-dimensional manifold. We equip this manifold with the Ebin metric, a natural metric structure for this space, to get a Riemannian manifold along with its associated geometric properties. We then use this Riemannian framework to apply object-oriented statistical analysis to define an atlas as the Fr\'echet mean of a population of Riemannian metrics. This formulation ties into the existing framework for diffeomorphic construction of image atlases, allowing us to construct a multimodal atlas by simultaneously integrating complementary white matter structure details from DWMRI and cortical details from T1-weighted MRI. We illustrate our framework with 2D data examples of connectome registration and atlas formation. Finally, we build an example 3D multimodal atlas using T1 images and connectomes derived from diffusion tensors estimated from a subset of subjects from the Human Connectome Project.

IoT Virtualization with ML-based Information Extraction

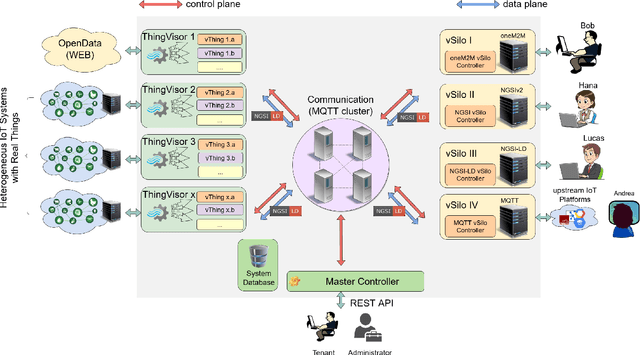
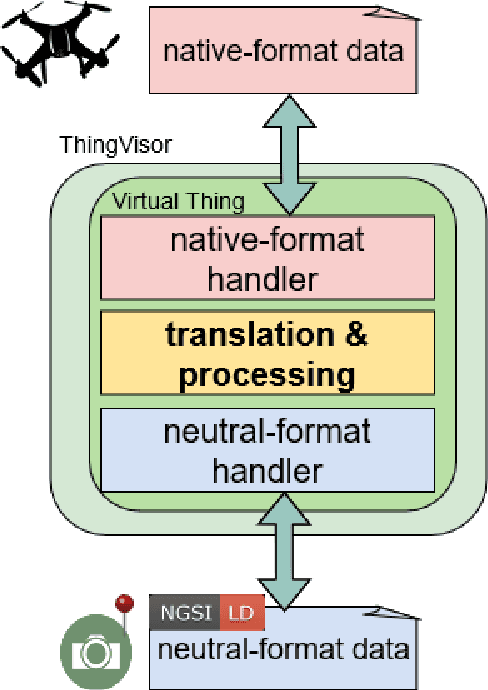
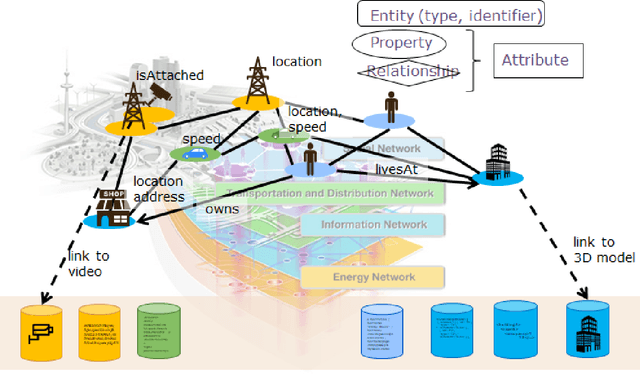
For IoT to reach its full potential, the sharing and reuse of information in different applications and across verticals is of paramount importance. However, there are a plethora of IoT platforms using different representations, protocols and interaction patterns. To address this issue, the Fed4IoT project has developed an IoT virtualization platform that, on the one hand, integrates information from many different source platforms and, on the other hand, makes the information required by the respective users available in the target platform of choice. To enable this, information is translated into a common, neutral exchange format. The format of choice is NGSI-LD, which is being standardized by the ETSI Industry Specification Group on Context Information Management (ETSI ISG CIM). Thing Visors are the components that translate the source information to NGSI-LD, which is then delivered to the target platform and translated into the target format. ThingVisors can be implemented by hand, but this requires significant human effort, especially considering the heterogeneity of low level information produced by a multitude of sensors. Thus, supporting the human developer and, ideally, fully automating the process of extracting and enriching data and translating it to NGSI-LD is a crucial step. Machine learning is a promising approach for this, but it typically requires large amounts of hand-labelled data for training, an effort that makes it unrealistic in many IoT scenarios. A programmatic labelling approach called knowledge infusion that encodes expert knowledge is used for matching a schema or ontology extracted from the data with a target schema or ontology, providing the basis for annotating the data and facilitating the translation to NGSI-LD.

Physics Informed Convex Artificial Neural Networks (PICANNs) for Optimal Transport based Density Estimation

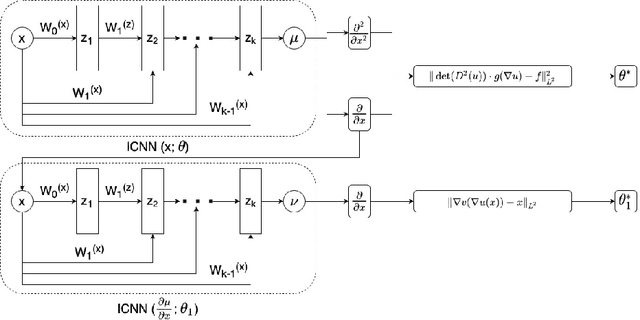
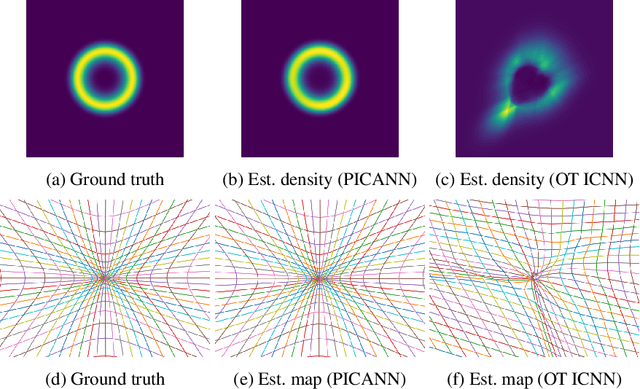
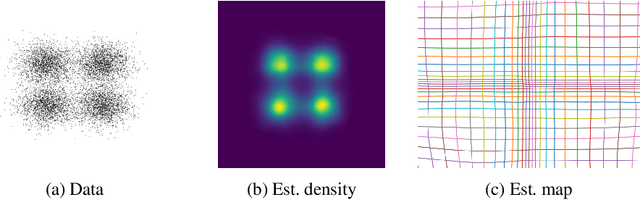
Optimal Mass Transport (OMT) is a well studied problem with a variety of applications in a diverse set of fields ranging from Physics to Computer Vision and in particular Statistics and Data Science. Since the original formulation of Monge in 1781 significant theoretical progress been made on the existence, uniqueness and properties of the optimal transport maps. The actual numerical computation of the transport maps, particularly in high dimensions, remains a challenging problem. By Brenier's theorem, the continuous OMT problem can be reduced to that of solving a non-linear PDE of Monge-Ampere type whose solution is a convex function. In this paper, building on recent developments of input convex neural networks and physics informed neural networks for solving PDE's, we propose a Deep Learning approach to solve the continuous OMT problem. To demonstrate the versatility of our framework we focus on the ubiquitous density estimation and generative modeling tasks in statistics and machine learning. Finally as an example we show how our framework can be incorporated with an autoencoder to estimate an effective probabilistic generative model.

Structural Connectome Atlas Construction in the Space of Riemannian Metrics

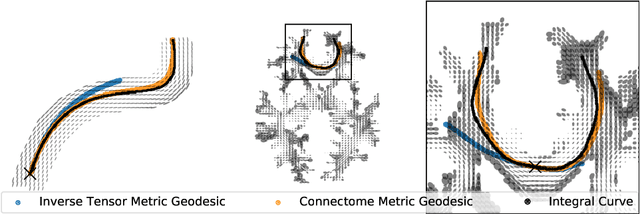
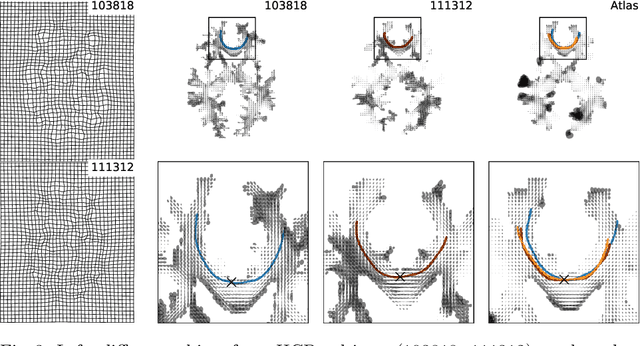
The structural connectome is often represented by fiber bundles generated from various types of tractography. We propose a method of analyzing connectomes by representing them as a Riemannian metric, thereby viewing them as points in an infinite-dimensional manifold. After equipping this space with a natural metric structure, the Ebin metric, we apply object-oriented statistical analysis to define an atlas as the Fr\'echet mean of a population of Riemannian metrics. We demonstrate connectome registration and atlas formation using connectomes derived from diffusion tensors estimated from a subset of subjects from the Human Connectome Project.