Emmanuel Hartman
Conic Formulations of Transport Metrics for Unbalanced Measure Networks and Hypernetworks
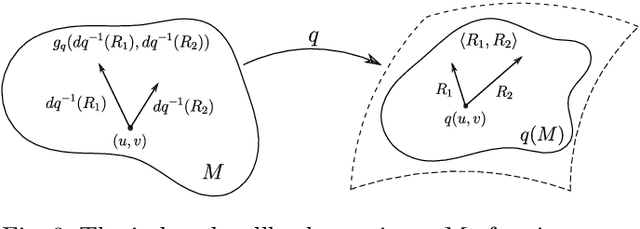
Aug 14, 2025Abstract:The Gromov-Wasserstein (GW) variant of optimal transport, designed to compare probability densities defined over distinct metric spaces, has emerged as an important tool for the analysis of data with complex structure, such as ensembles of point clouds or networks. To overcome certain limitations, such as the restriction to comparisons of measures of equal mass and sensitivity to outliers, several unbalanced or partial transport relaxations of the GW distance have been introduced in the recent literature. This paper is concerned with the Conic Gromov-Wasserstein (CGW) distance introduced by S\'{e}journ\'{e}, Vialard, and Peyr\'{e}. We provide a novel formulation in terms of semi-couplings, and extend the framework beyond the metric measure space setting, to compare more general network and hypernetwork structures. With this new formulation, we establish several fundamental properties of the CGW metric, including its scaling behavior under dilation, variational convergence in the limit of volume growth constraints, and comparison bounds with established optimal transport metrics. We further derive quantitative bounds that characterize the robustness of the CGW metric to perturbations in the underlying measures. The hypernetwork formulation of CGW admits a simple and provably convergent block coordinate ascent algorithm for its estimation, and we demonstrate the computational tractability and scalability of our approach through experiments on synthetic and real-world high-dimensional and structured datasets.
Self Supervised Networks for Learning Latent Space Representations of Human Body Scans and Motions
Nov 05, 2024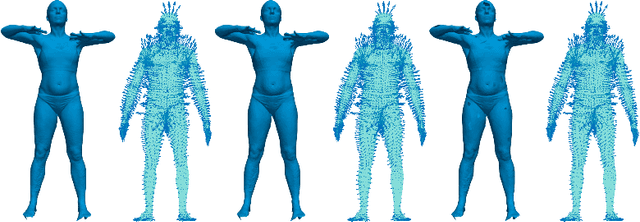


Abstract:This paper introduces self-supervised neural network models to tackle several fundamental problems in the field of 3D human body analysis and processing. First, we propose VariShaPE (Varifold Shape Parameter Estimator), a novel architecture for the retrieval of latent space representations of body shapes and poses. This network offers a fast and robust method to estimate the embedding of arbitrary unregistered meshes into the latent space. Second, we complement the estimation of latent codes with MoGeN (Motion Geometry Network) a framework that learns the geometry on the latent space itself. This is achieved by lifting the body pose parameter space into a higher dimensional Euclidean space in which body motion mini-sequences from a training set of 4D data can be approximated by simple linear interpolation. Using the SMPL latent space representation we illustrate how the combination of these network models, once trained, can be used to perform a variety of tasks with very limited computational cost. This includes operations such as motion interpolation, extrapolation and transfer as well as random shape and pose generation.
Basis restricted elastic shape analysis on the space of unregistered surfaces
Nov 07, 2023Abstract:This paper introduces a new mathematical and numerical framework for surface analysis derived from the general setting of elastic Riemannian metrics on shape spaces. Traditionally, those metrics are defined over the infinite dimensional manifold of immersed surfaces and satisfy specific invariance properties enabling the comparison of surfaces modulo shape preserving transformations such as reparametrizations. The specificity of the approach we develop is to restrict the space of allowable transformations to predefined finite dimensional bases of deformation fields. These are estimated in a data-driven way so as to emulate specific types of surface transformations observed in a training set. The use of such bases allows to simplify the representation of the corresponding shape space to a finite dimensional latent space. However, in sharp contrast with methods involving e.g. mesh autoencoders, the latent space is here equipped with a non-Euclidean Riemannian metric precisely inherited from the family of aforementioned elastic metrics. We demonstrate how this basis restricted model can be then effectively implemented to perform a variety of tasks on surface meshes which, importantly, does not assume these to be pre-registered (i.e. with given point correspondences) or to even have a consistent mesh structure. We specifically validate our approach on human body shape and pose data as well as human face scans, and show how it generally outperforms state-of-the-art methods on problems such as shape registration, interpolation, motion transfer or random pose generation.
VariGrad: A Novel Feature Vector Architecture for Geometric Deep Learning on Unregistered Data
Jul 07, 2023



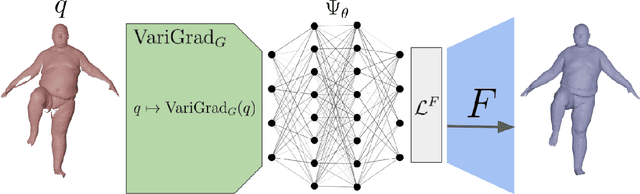
Abstract:We present a novel geometric deep learning layer that leverages the varifold gradient (VariGrad) to compute feature vector representations of 3D geometric data. These feature vectors can be used in a variety of downstream learning tasks such as classification, registration, and shape reconstruction. Our model's use of parameterization independent varifold representations of geometric data allows our model to be both trained and tested on data independent of the given sampling or parameterization. We demonstrate the efficiency, generalizability, and robustness to resampling demonstrated by the proposed VariGrad layer.
BaRe-ESA: A Riemannian Framework for Unregistered Human Body Shapes
Nov 23, 2022



Abstract:We present BaRe-ESA, a novel Riemannian framework for human body scan representation, interpolation and extrapolation. BaRe-ESA operates directly on unregistered meshes, i.e., without the need to establish prior point to point correspondences or to assume a consistent mesh structure. Our method relies on a latent space representation, which is equipped with a Riemannian (non-Euclidean) metric associated to an invariant higher-order metric on the space of surfaces. Experimental results on the FAUST and DFAUST datasets show that BaRe-ESA brings significant improvements with respect to previous solutions in terms of shape registration, interpolation and extrapolation. The efficiency and strength of our model is further demonstrated in applications such as motion transfer and random generation of body shape and pose.
Elastic shape analysis of surfaces with second-order Sobolev metrics: a comprehensive numerical framework
Apr 08, 2022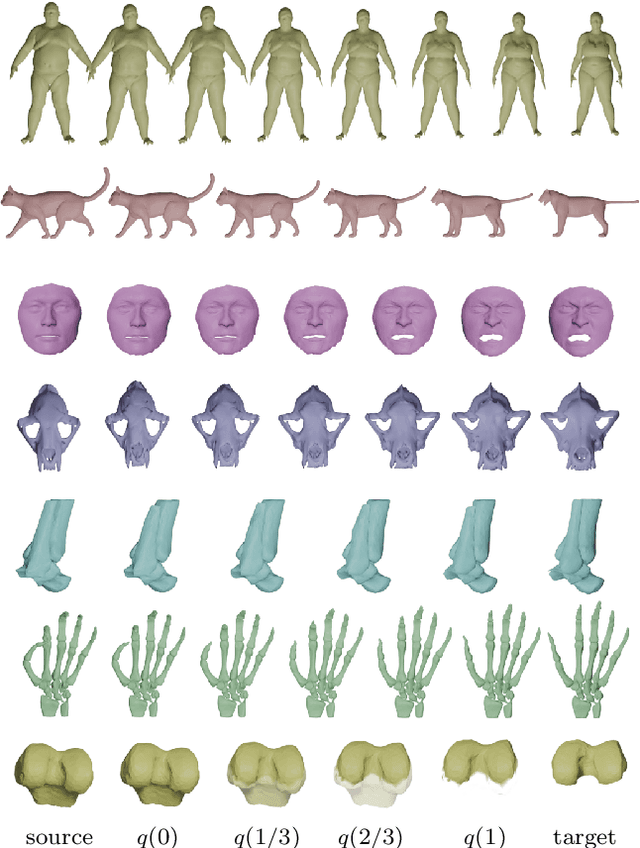
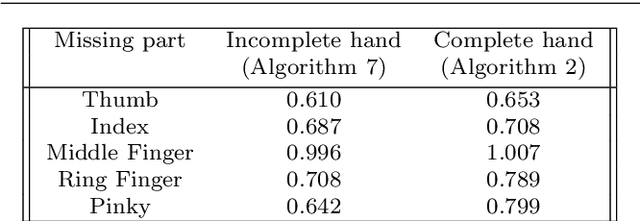

Abstract:This paper introduces a set of numerical methods for Riemannian shape analysis of 3D surfaces within the setting of invariant (elastic) second-order Sobolev metrics. More specifically, we address the computation of geodesics and geodesic distances between parametrized or unparametrized immersed surfaces represented as 3D meshes. Building on this, we develop tools for the statistical shape analysis of sets of surfaces, including methods for estimating Karcher means and performing tangent PCA on shape populations, and for computing parallel transport along paths of surfaces. Our proposed approach fundamentally relies on a relaxed variational formulation for the geodesic matching problem via the use of varifold fidelity terms, which enable us to enforce reparametrization independence when computing geodesics between unparametrized surfaces, while also yielding versatile algorithms that allow us to compare surfaces with varying sampling or mesh structures. Importantly, we demonstrate how our relaxed variational framework can be extended to tackle partially observed data. The different benefits of our numerical pipeline are illustrated over various examples, synthetic and real.
Supervised deep learning of elastic SRV distances on the shape space of curves
Jan 13, 2021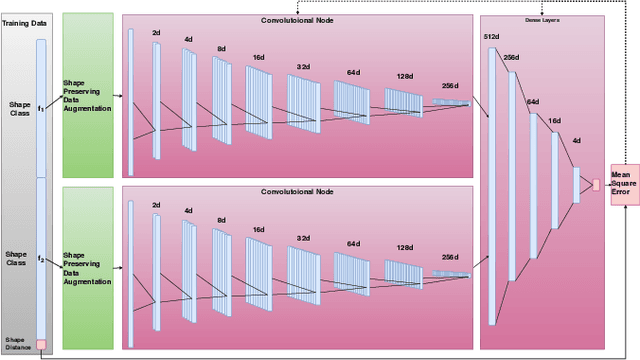
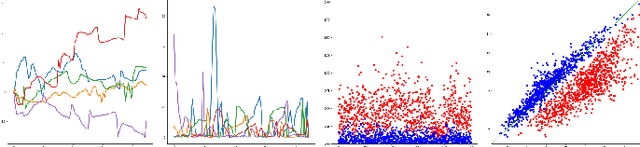
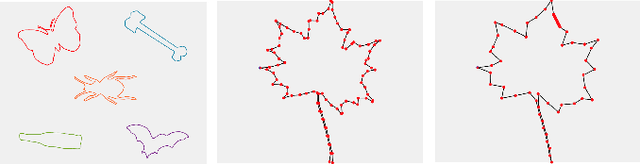
Abstract:Motivated by applications from computer vision to bioinformatics, the field of shape analysis deals with problems where one wants to analyze geometric objects, such as curves, while ignoring actions that preserve their shape, such as translations, rotations, or reparametrizations. Mathematical tools have been developed to define notions of distances, averages, and optimal deformations for geometric objects. One such framework, which has proven to be successful in many applications, is based on the square root velocity (SRV) transform, which allows one to define a computable distance between spatial curves regardless of how they are parametrized. This paper introduces a supervised deep learning framework for the direct computation of SRV distances between curves, which usually requires an optimization over the group of reparametrizations that act on the curves. The benefits of our approach in terms of computational speed and accuracy are illustrated via several numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge