Learning the Night Sky with Deep Generative Priors

Recovering sharper images from blurred observations, referred to as deconvolution, is an ill-posed problem where classical approaches often produce unsatisfactory results. In ground-based astronomy, combining multiple exposures to achieve images with higher signal-to-noise ratios is complicated by the variation of point-spread functions across exposures due to atmospheric effects. We develop an unsupervised multi-frame method for denoising, deblurring, and coadding images inspired by deep generative priors. We use a carefully chosen convolutional neural network architecture that combines information from multiple observations, regularizes the joint likelihood over these observations, and allows us to impose desired constraints, such as non-negativity of pixel values in the sharp, restored image. With an eye towards the Rubin Observatory, we analyze 4K by 4K Hyper Suprime-Cam exposures and obtain preliminary results which yield promising restored images and extracted source lists.

Elastic shape analysis of surfaces with second-order Sobolev metrics: a comprehensive numerical framework

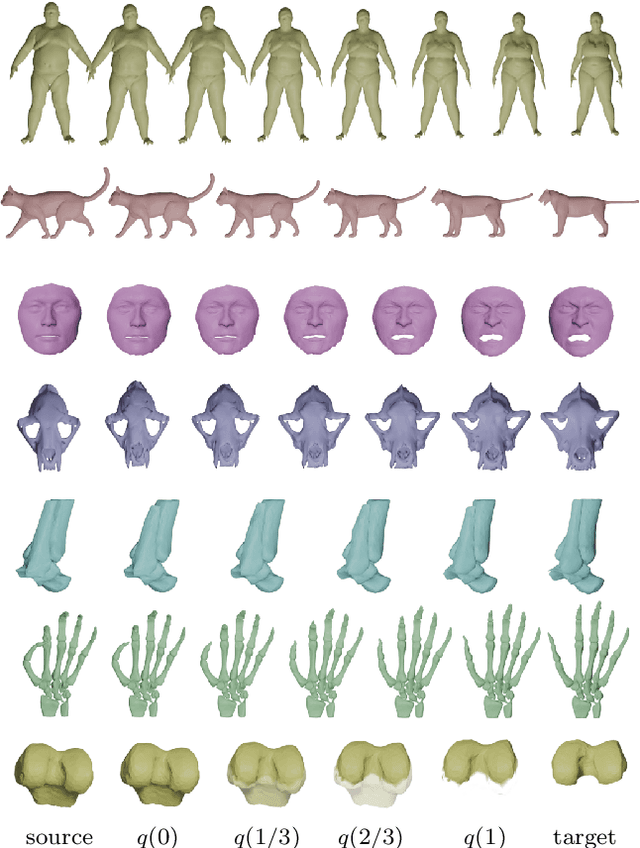
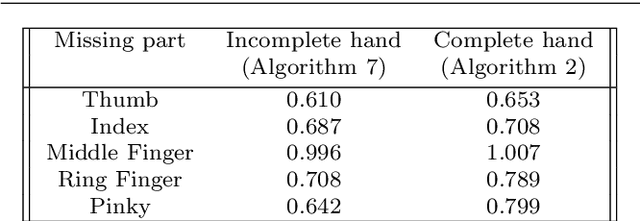
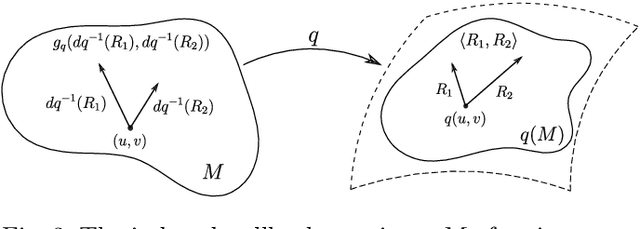
This paper introduces a set of numerical methods for Riemannian shape analysis of 3D surfaces within the setting of invariant (elastic) second-order Sobolev metrics. More specifically, we address the computation of geodesics and geodesic distances between parametrized or unparametrized immersed surfaces represented as 3D meshes. Building on this, we develop tools for the statistical shape analysis of sets of surfaces, including methods for estimating Karcher means and performing tangent PCA on shape populations, and for computing parallel transport along paths of surfaces. Our proposed approach fundamentally relies on a relaxed variational formulation for the geodesic matching problem via the use of varifold fidelity terms, which enable us to enforce reparametrization independence when computing geodesics between unparametrized surfaces, while also yielding versatile algorithms that allow us to compare surfaces with varying sampling or mesh structures. Importantly, we demonstrate how our relaxed variational framework can be extended to tackle partially observed data. The different benefits of our numerical pipeline are illustrated over various examples, synthetic and real.

Supervised deep learning of elastic SRV distances on the shape space of curves

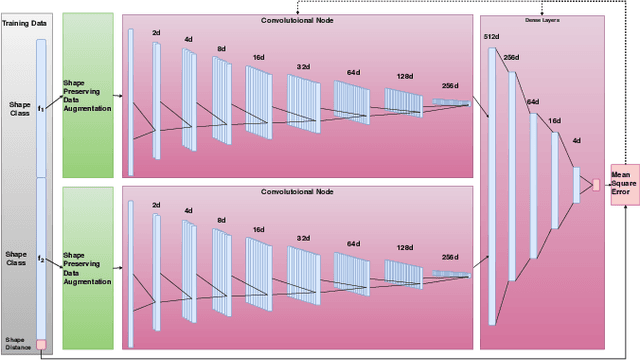
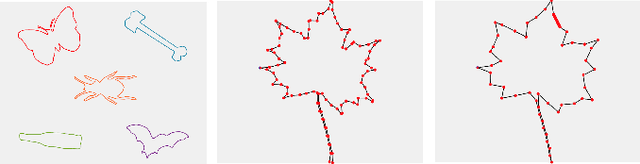
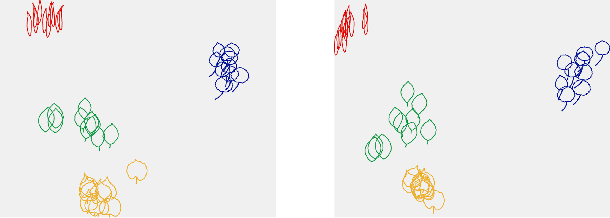
Motivated by applications from computer vision to bioinformatics, the field of shape analysis deals with problems where one wants to analyze geometric objects, such as curves, while ignoring actions that preserve their shape, such as translations, rotations, or reparametrizations. Mathematical tools have been developed to define notions of distances, averages, and optimal deformations for geometric objects. One such framework, which has proven to be successful in many applications, is based on the square root velocity (SRV) transform, which allows one to define a computable distance between spatial curves regardless of how they are parametrized. This paper introduces a supervised deep learning framework for the direct computation of SRV distances between curves, which usually requires an optimization over the group of reparametrizations that act on the curves. The benefits of our approach in terms of computational speed and accuracy are illustrated via several numerical experiments.

An inexact matching approach for the comparison of plane curves with general elastic metrics

This paper introduces a new mathematical formulation and numerical approach for the computation of distances and geodesics between immersed planar curves. Our approach combines the general simplifying transform for first-order elastic metrics that was recently introduced by Kurtek and Needham, together with a relaxation of the matching constraint using parametrization-invariant fidelity metrics. The main advantages of this formulation are that it leads to a simple optimization problem for discretized curves, and that it provides a flexible approach to deal with noisy, inconsistent or corrupted data. These benefits are illustrated via a few preliminary numerical results.