Diffeomorphic Latent Neural Operators for Data-Efficient Learning of Solutions to Partial Differential Equations

A computed approximation of the solution operator to a system of partial differential equations (PDEs) is needed in various areas of science and engineering. Neural operators have been shown to be quite effective at predicting these solution generators after training on high-fidelity ground truth data (e.g. numerical simulations). However, in order to generalize well to unseen spatial domains, neural operators must be trained on an extensive amount of geometrically varying data samples that may not be feasible to acquire or simulate in certain contexts (e.g., patient-specific medical data, large-scale computationally intensive simulations.) We propose that in order to learn a PDE solution operator that can generalize across multiple domains without needing to sample enough data expressive enough for all possible geometries, we can train instead a latent neural operator on just a few ground truth solution fields diffeomorphically mapped from different geometric/spatial domains to a fixed reference configuration. Furthermore, the form of the solutions is dependent on the choice of mapping to and from the reference domain. We emphasize that preserving properties of the differential operator when constructing these mappings can significantly reduce the data requirement for achieving an accurate model due to the regularity of the solution fields that the latent neural operator is training on. We provide motivating numerical experimentation that demonstrates an extreme case of this consideration by exploiting the conformal invariance of the Laplacian

Diffeomorphic Latent Neural Operator Learning for Data-Efficient Predictions of Solutions to Partial Differential Equations

A computed approximation of the solution operator to a system of partial differential equations (PDEs) is needed in various areas of science and engineering. Neural operators have been shown to be quite effective at predicting these solution generators after training on high-fidelity ground truth data (e.g. numerical simulations). However, in order to generalize well to unseen spatial domains, neural operators must be trained on an extensive amount of geometrically varying data samples that may not be feasible to acquire or simulate in certain contexts (i.e., patient-specific medical data, large-scale computationally intensive simulations.) We propose that in order to learn a PDE solution operator that can generalize across multiple domains without needing to sample enough data expressive enough for all possible geometries, we can train instead a latent neural operator on just a few ground truth solution fields diffeomorphically mapped from different geometric/spatial domains to a fixed reference configuration. Furthermore, the form of the solutions is dependent on the choice of mapping to and from the reference domain. We emphasize that preserving properties of the differential operator when constructing these mappings can significantly reduce the data requirement for achieving an accurate model due to the regularity of the solution fields that the latent neural operator is training on. We provide motivating numerical experimentation that demonstrates an extreme case of this consideration by exploiting the conformal invariance of the Laplacian

Self Supervised Networks for Learning Latent Space Representations of Human Body Scans and Motions

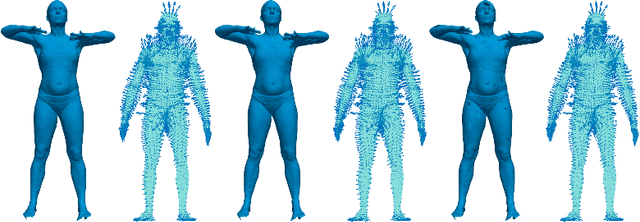
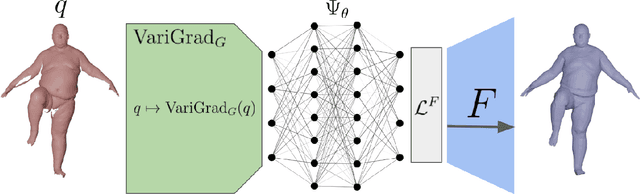
This paper introduces self-supervised neural network models to tackle several fundamental problems in the field of 3D human body analysis and processing. First, we propose VariShaPE (Varifold Shape Parameter Estimator), a novel architecture for the retrieval of latent space representations of body shapes and poses. This network offers a fast and robust method to estimate the embedding of arbitrary unregistered meshes into the latent space. Second, we complement the estimation of latent codes with MoGeN (Motion Geometry Network) a framework that learns the geometry on the latent space itself. This is achieved by lifting the body pose parameter space into a higher dimensional Euclidean space in which body motion mini-sequences from a training set of 4D data can be approximated by simple linear interpolation. Using the SMPL latent space representation we illustrate how the combination of these network models, once trained, can be used to perform a variety of tasks with very limited computational cost. This includes operations such as motion interpolation, extrapolation and transfer as well as random shape and pose generation.

DIMON: Learning Solution Operators of Partial Differential Equations on a Diffeomorphic Family of Domains

The solution of a PDE over varying initial/boundary conditions on multiple domains is needed in a wide variety of applications, but it is computationally expensive if the solution is computed de novo whenever the initial/boundary conditions of the domain change. We introduce a general operator learning framework, called DIffeomorphic Mapping Operator learNing (DIMON) to learn approximate PDE solutions over a family of domains $\{\Omega_{\theta}}_\theta$, that learns the map from initial/boundary conditions and domain $\Omega_\theta$ to the solution of the PDE, or to specified functionals thereof. DIMON is based on transporting a given problem (initial/boundary conditions and domain $\Omega_{\theta}$) to a problem on a reference domain $\Omega_{0}$, where training data from multiple problems is used to learn the map to the solution on $\Omega_{0}$, which is then re-mapped to the original domain $\Omega_{\theta}$. We consider several problems to demonstrate the performance of the framework in learning both static and time-dependent PDEs on non-rigid geometries; these include solving the Laplace equation, reaction-diffusion equations, and a multiscale PDE that characterizes the electrical propagation on the left ventricle. This work paves the way toward the fast prediction of PDE solutions on a family of domains and the application of neural operators in engineering and precision medicine.

Basis restricted elastic shape analysis on the space of unregistered surfaces

This paper introduces a new mathematical and numerical framework for surface analysis derived from the general setting of elastic Riemannian metrics on shape spaces. Traditionally, those metrics are defined over the infinite dimensional manifold of immersed surfaces and satisfy specific invariance properties enabling the comparison of surfaces modulo shape preserving transformations such as reparametrizations. The specificity of the approach we develop is to restrict the space of allowable transformations to predefined finite dimensional bases of deformation fields. These are estimated in a data-driven way so as to emulate specific types of surface transformations observed in a training set. The use of such bases allows to simplify the representation of the corresponding shape space to a finite dimensional latent space. However, in sharp contrast with methods involving e.g. mesh autoencoders, the latent space is here equipped with a non-Euclidean Riemannian metric precisely inherited from the family of aforementioned elastic metrics. We demonstrate how this basis restricted model can be then effectively implemented to perform a variety of tasks on surface meshes which, importantly, does not assume these to be pre-registered (i.e. with given point correspondences) or to even have a consistent mesh structure. We specifically validate our approach on human body shape and pose data as well as human face scans, and show how it generally outperforms state-of-the-art methods on problems such as shape registration, interpolation, motion transfer or random pose generation.

BaRe-ESA: A Riemannian Framework for Unregistered Human Body Shapes

We present BaRe-ESA, a novel Riemannian framework for human body scan representation, interpolation and extrapolation. BaRe-ESA operates directly on unregistered meshes, i.e., without the need to establish prior point to point correspondences or to assume a consistent mesh structure. Our method relies on a latent space representation, which is equipped with a Riemannian (non-Euclidean) metric associated to an invariant higher-order metric on the space of surfaces. Experimental results on the FAUST and DFAUST datasets show that BaRe-ESA brings significant improvements with respect to previous solutions in terms of shape registration, interpolation and extrapolation. The efficiency and strength of our model is further demonstrated in applications such as motion transfer and random generation of body shape and pose.

A Diffeomorphic Flow-based Variational Framework for Multi-speaker Emotion Conversion

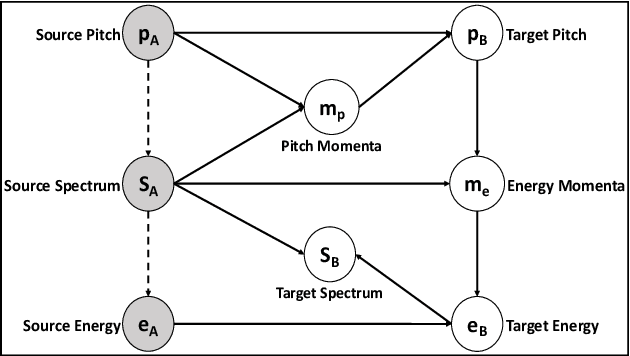
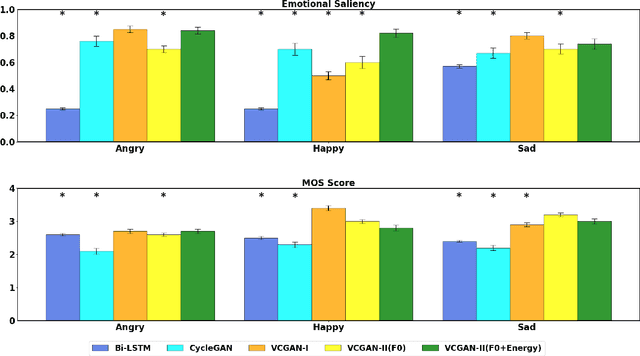
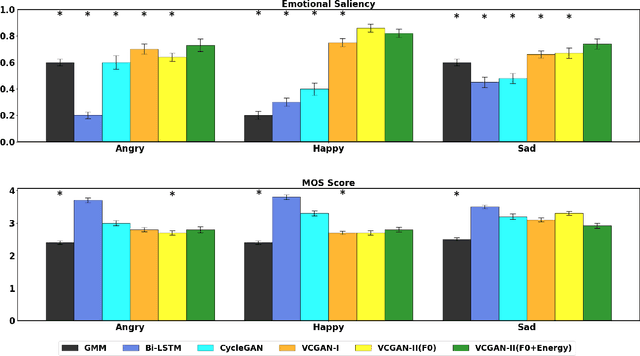
This paper introduces a new framework for non-parallel emotion conversion in speech. Our framework is based on two key contributions. First, we propose a stochastic version of the popular CycleGAN model. Our modified loss function introduces a Kullback Leibler (KL) divergence term that aligns the source and target data distributions learned by the generators, thus overcoming the limitations of sample wise generation. By using a variational approximation to this stochastic loss function, we show that our KL divergence term can be implemented via a paired density discriminator. We term this new architecture a variational CycleGAN (VCGAN). Second, we model the prosodic features of target emotion as a smooth and learnable deformation of the source prosodic features. This approach provides implicit regularization that offers key advantages in terms of better range alignment to unseen and out of distribution speakers. We conduct rigorous experiments and comparative studies to demonstrate that our proposed framework is fairly robust with high performance against several state-of-the-art baselines.

Elastic shape analysis of surfaces with second-order Sobolev metrics: a comprehensive numerical framework

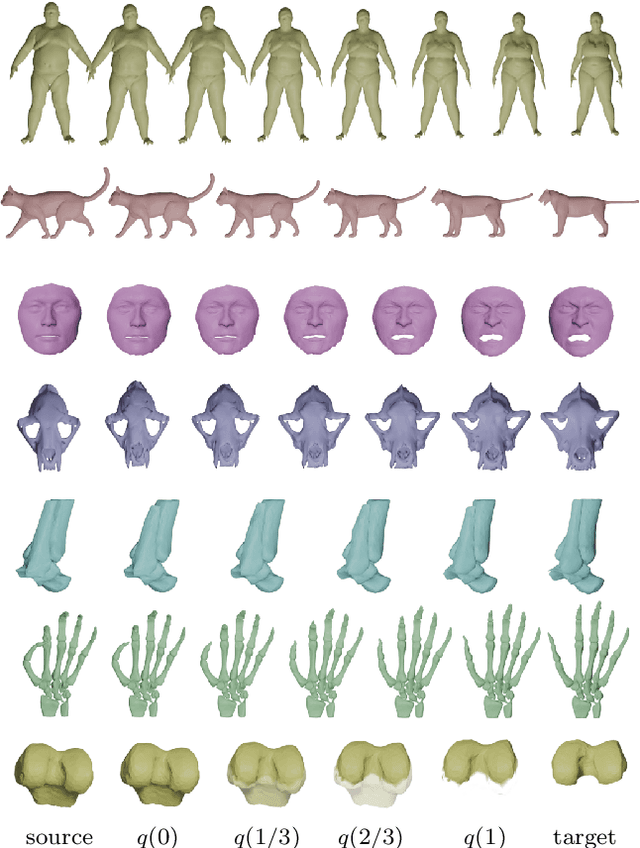
This paper introduces a set of numerical methods for Riemannian shape analysis of 3D surfaces within the setting of invariant (elastic) second-order Sobolev metrics. More specifically, we address the computation of geodesics and geodesic distances between parametrized or unparametrized immersed surfaces represented as 3D meshes. Building on this, we develop tools for the statistical shape analysis of sets of surfaces, including methods for estimating Karcher means and performing tangent PCA on shape populations, and for computing parallel transport along paths of surfaces. Our proposed approach fundamentally relies on a relaxed variational formulation for the geodesic matching problem via the use of varifold fidelity terms, which enable us to enforce reparametrization independence when computing geodesics between unparametrized surfaces, while also yielding versatile algorithms that allow us to compare surfaces with varying sampling or mesh structures. Importantly, we demonstrate how our relaxed variational framework can be extended to tackle partially observed data. The different benefits of our numerical pipeline are illustrated over various examples, synthetic and real.

Supervised deep learning of elastic SRV distances on the shape space of curves

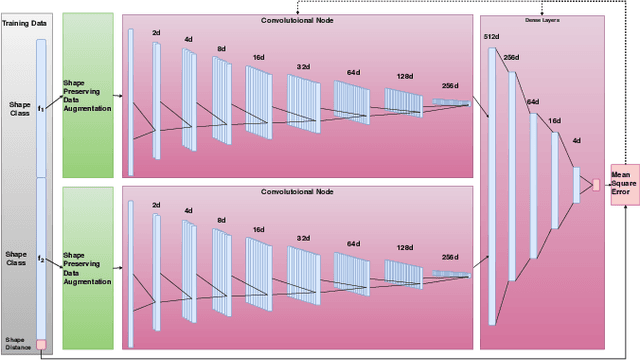
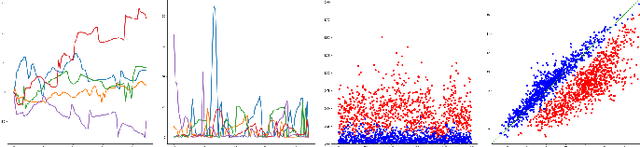
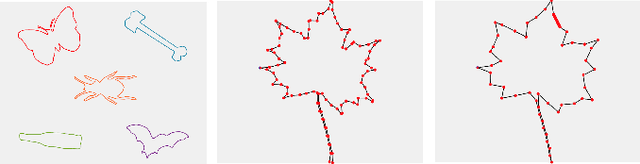
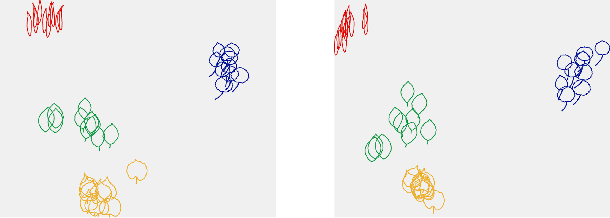
Motivated by applications from computer vision to bioinformatics, the field of shape analysis deals with problems where one wants to analyze geometric objects, such as curves, while ignoring actions that preserve their shape, such as translations, rotations, or reparametrizations. Mathematical tools have been developed to define notions of distances, averages, and optimal deformations for geometric objects. One such framework, which has proven to be successful in many applications, is based on the square root velocity (SRV) transform, which allows one to define a computable distance between spatial curves regardless of how they are parametrized. This paper introduces a supervised deep learning framework for the direct computation of SRV distances between curves, which usually requires an optimization over the group of reparametrizations that act on the curves. The benefits of our approach in terms of computational speed and accuracy are illustrated via several numerical experiments.

Multi-speaker Emotion Conversion via Latent Variable Regularization and a Chained Encoder-Decoder-Predictor Network

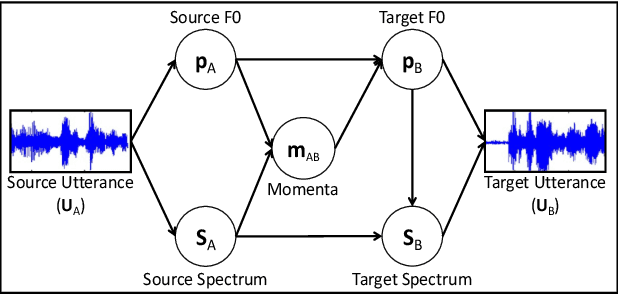
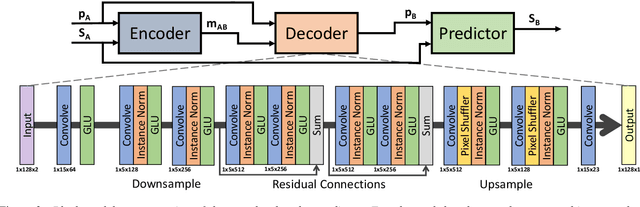
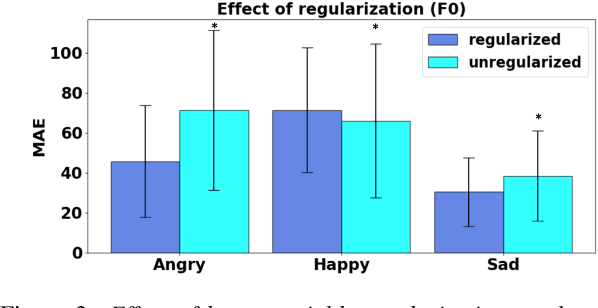
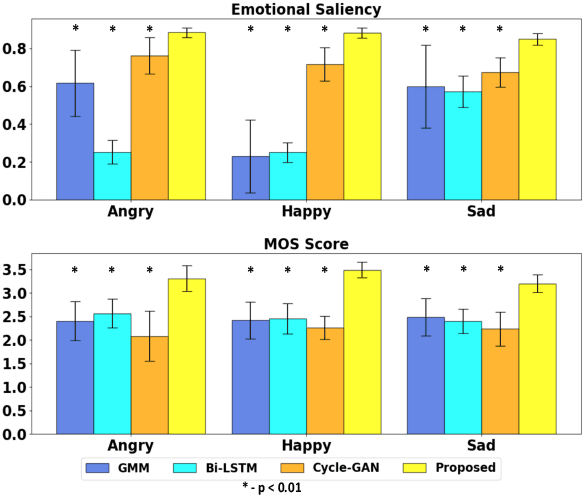
We propose a novel method for emotion conversion in speech based on a chained encoder-decoder-predictor neural network architecture. The encoder constructs a latent embedding of the fundamental frequency (F0) contour and the spectrum, which we regularize using the Large Diffeomorphic Metric Mapping (LDDMM) registration framework. The decoder uses this embedding to predict the modified F0 contour in a target emotional class. Finally, the predictor uses the original spectrum and the modified F0 contour to generate a corresponding target spectrum. Our joint objective function simultaneously optimizes the parameters of three model blocks. We show that our method outperforms the existing state-of-the-art approaches on both, the saliency of emotion conversion and the quality of resynthesized speech. In addition, the LDDMM regularization allows our model to convert phrases that were not present in training, thus providing evidence for out-of-sample generalization.