A Diffeomorphic Flow-based Variational Framework for Multi-speaker Emotion Conversion

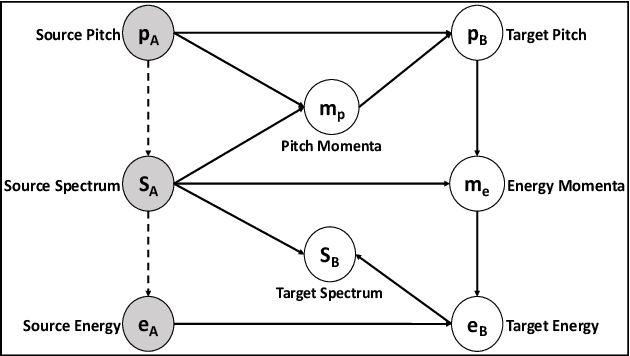
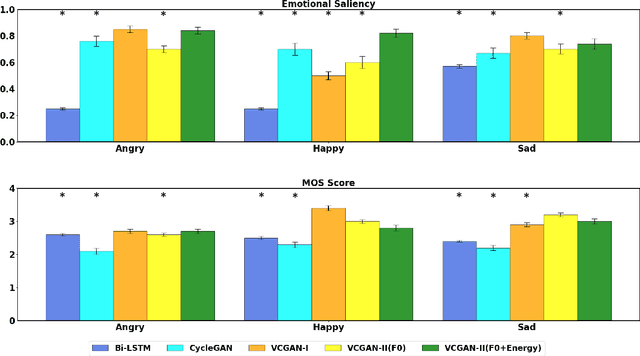
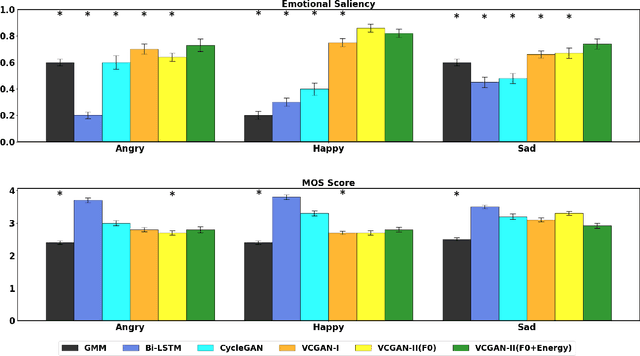
This paper introduces a new framework for non-parallel emotion conversion in speech. Our framework is based on two key contributions. First, we propose a stochastic version of the popular CycleGAN model. Our modified loss function introduces a Kullback Leibler (KL) divergence term that aligns the source and target data distributions learned by the generators, thus overcoming the limitations of sample wise generation. By using a variational approximation to this stochastic loss function, we show that our KL divergence term can be implemented via a paired density discriminator. We term this new architecture a variational CycleGAN (VCGAN). Second, we model the prosodic features of target emotion as a smooth and learnable deformation of the source prosodic features. This approach provides implicit regularization that offers key advantages in terms of better range alignment to unseen and out of distribution speakers. We conduct rigorous experiments and comparative studies to demonstrate that our proposed framework is fairly robust with high performance against several state-of-the-art baselines.

Multi-speaker Emotion Conversion via Latent Variable Regularization and a Chained Encoder-Decoder-Predictor Network

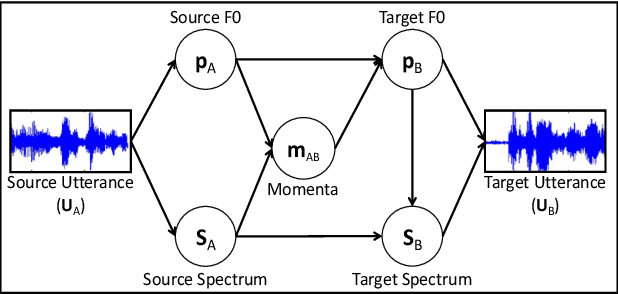
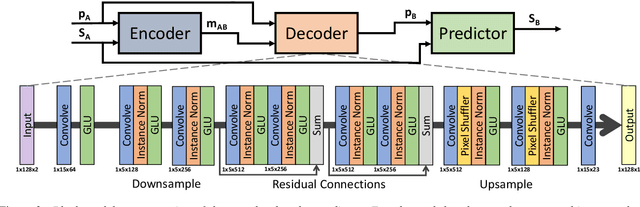
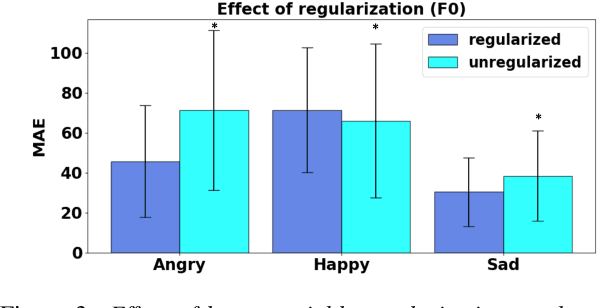
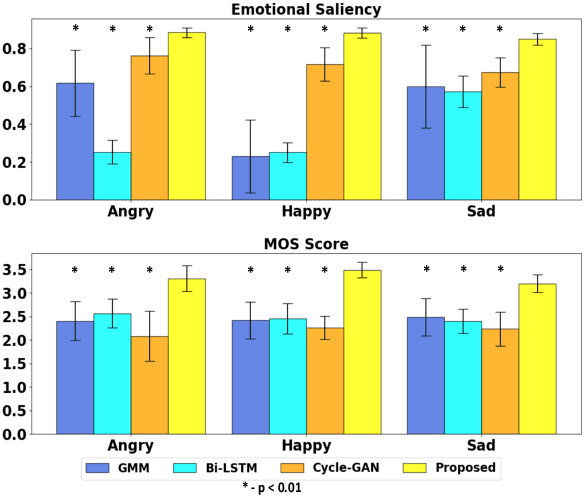
We propose a novel method for emotion conversion in speech based on a chained encoder-decoder-predictor neural network architecture. The encoder constructs a latent embedding of the fundamental frequency (F0) contour and the spectrum, which we regularize using the Large Diffeomorphic Metric Mapping (LDDMM) registration framework. The decoder uses this embedding to predict the modified F0 contour in a target emotional class. Finally, the predictor uses the original spectrum and the modified F0 contour to generate a corresponding target spectrum. Our joint objective function simultaneously optimizes the parameters of three model blocks. We show that our method outperforms the existing state-of-the-art approaches on both, the saliency of emotion conversion and the quality of resynthesized speech. In addition, the LDDMM regularization allows our model to convert phrases that were not present in training, thus providing evidence for out-of-sample generalization.

A numerical framework for elastic surface matching, comparison, and interpolation

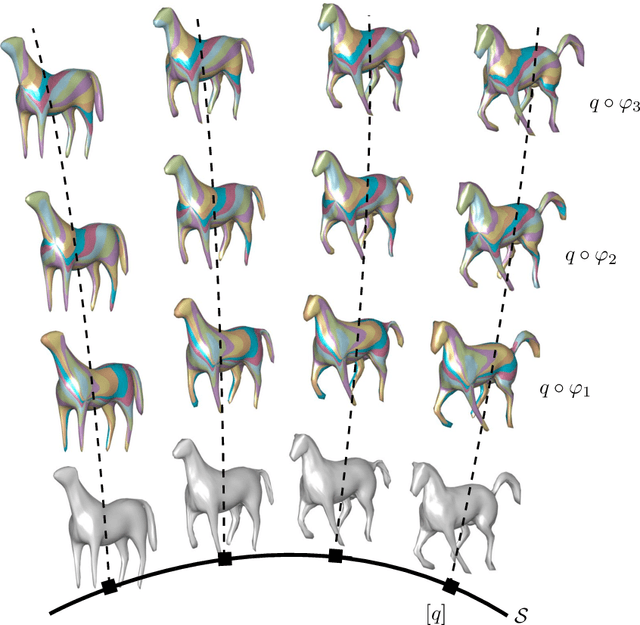
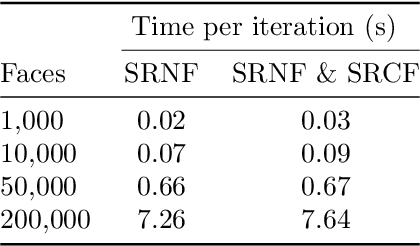
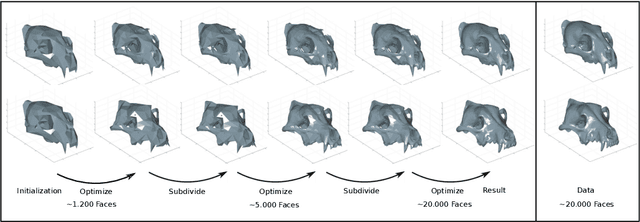
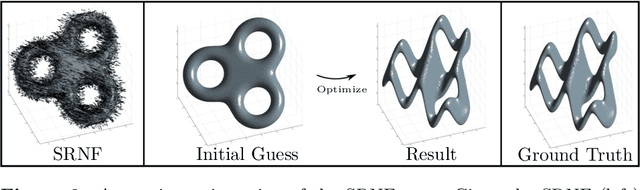
Surface comparison and matching is a challenging problem in computer vision. While reparametrization-invariant Sobolev metrics provide meaningful elastic distances and point correspondences via the geodesic boundary value problem, solving this problem numerically tends to be difficult. Square root normal fields (SRNF) considerably simplify the computation of certain elastic distances between parametrized surfaces. Yet they leave open the issue of finding optimal reparametrizations, which induce elastic distances between unparametrized surfaces. This issue has concentrated much effort in recent years and led to the development of several numerical frameworks. In this paper, we take an alternative approach which bypasses the direct estimation of reparametrizations: we relax the geodesic boundary constraint using an auxiliary parametrization-blind varifold fidelity metric. This reformulation has several notable benefits. By avoiding altogether the need for reparametrizations, it provides the flexibility to deal with simplicial meshes of arbitrary topologies and sampling patterns. Moreover, the problem lends itself to a coarse-to-fine multi-resolution implementation, which makes the algorithm scalable to large meshes. Furthermore, this approach extends readily to higher-order feature maps such as square root curvature fields and is also able to include surface textures in the matching problem. We demonstrate these advantages on several examples, synthetic and real.