A numerical framework for elastic surface matching, comparison, and interpolation

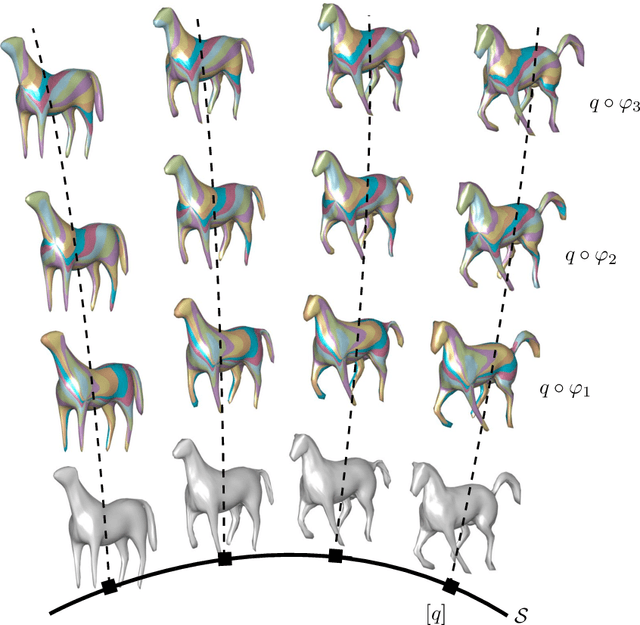
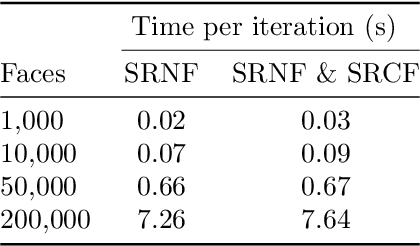
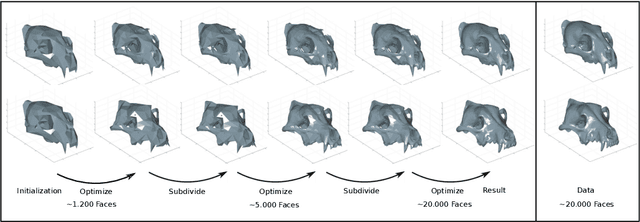
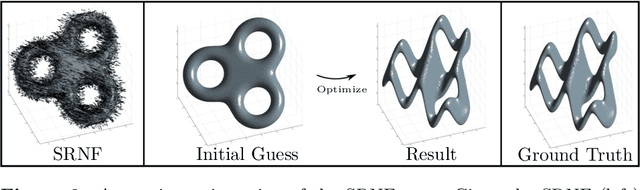
Surface comparison and matching is a challenging problem in computer vision. While reparametrization-invariant Sobolev metrics provide meaningful elastic distances and point correspondences via the geodesic boundary value problem, solving this problem numerically tends to be difficult. Square root normal fields (SRNF) considerably simplify the computation of certain elastic distances between parametrized surfaces. Yet they leave open the issue of finding optimal reparametrizations, which induce elastic distances between unparametrized surfaces. This issue has concentrated much effort in recent years and led to the development of several numerical frameworks. In this paper, we take an alternative approach which bypasses the direct estimation of reparametrizations: we relax the geodesic boundary constraint using an auxiliary parametrization-blind varifold fidelity metric. This reformulation has several notable benefits. By avoiding altogether the need for reparametrizations, it provides the flexibility to deal with simplicial meshes of arbitrary topologies and sampling patterns. Moreover, the problem lends itself to a coarse-to-fine multi-resolution implementation, which makes the algorithm scalable to large meshes. Furthermore, this approach extends readily to higher-order feature maps such as square root curvature fields and is also able to include surface textures in the matching problem. We demonstrate these advantages on several examples, synthetic and real.