Deep dynamic modeling with just two time points: Can we still allow for individual trajectories?

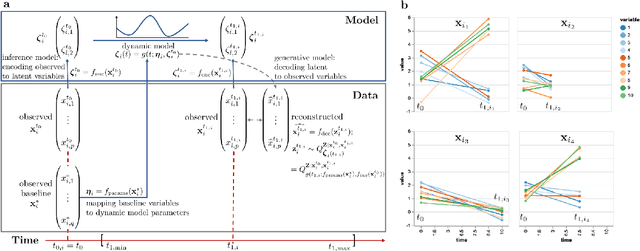
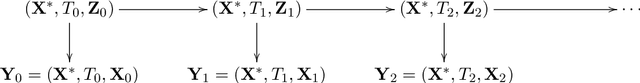
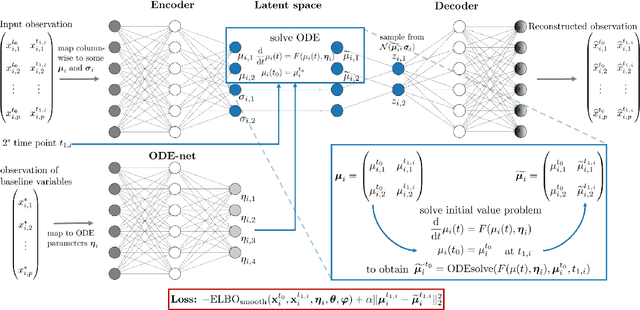
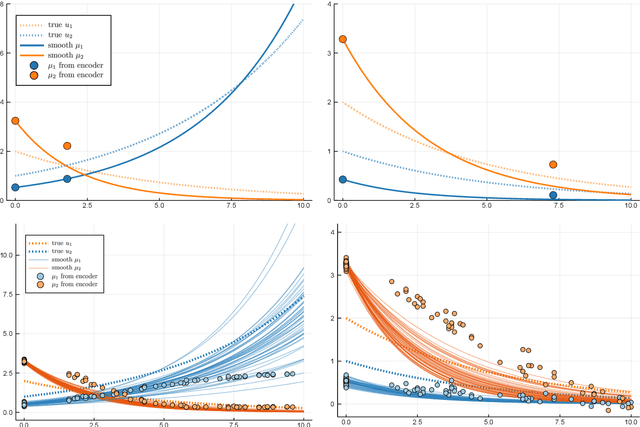
Longitudinal biomedical data are often characterized by a sparse time grid and individual-specific development patterns. Specifically, in epidemiological cohort studies and clinical registries we are facing the question of what can be learned from the data in an early phase of the study, when only a baseline characterization and one follow-up measurement are available. Inspired by recent advances that allow to combine deep learning with dynamic modeling, we investigate whether such approaches can be useful for uncovering complex structure, in particular for an extreme small data setting with only two observations time points for each individual. Irregular spacing in time could then be used to gain more information on individual dynamics by leveraging similarity of individuals. We provide a brief overview of how variational autoencoders (VAEs), as a deep learning approach, can be linked to ordinary differential equations (ODEs) for dynamic modeling, and then specifically investigate the feasibility of such an approach that infers individual-specific latent trajectories by including regularity assumptions and individuals' similarity. We also provide a description of this deep learning approach as a filtering task to give a statistical perspective. Using simulated data, we show to what extent the approach can recover individual trajectories from ODE systems with two and four unknown parameters and infer groups of individuals with similar trajectories, and where it breaks down. The results show that such dynamic deep learning approaches can be useful even in extreme small data settings, but need to be carefully adapted.

A numerical framework for elastic surface matching, comparison, and interpolation

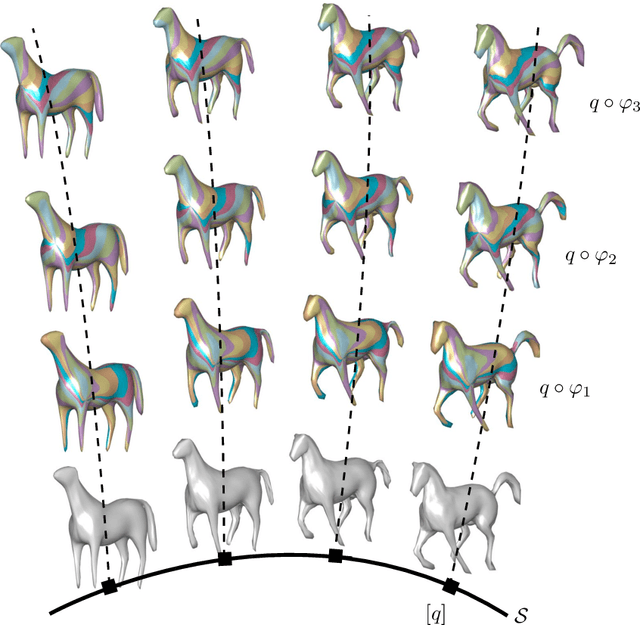
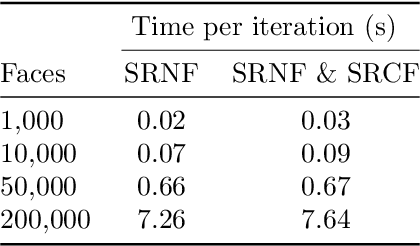
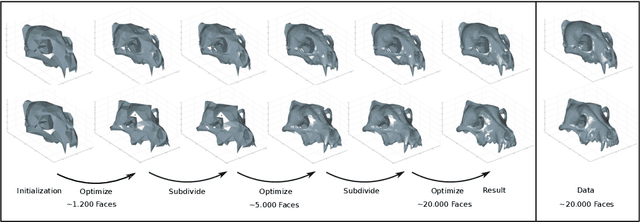
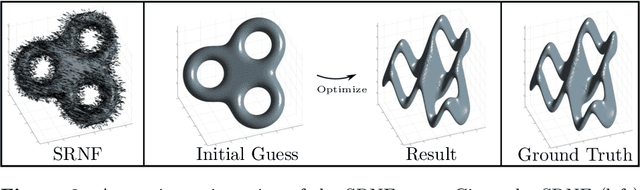
Surface comparison and matching is a challenging problem in computer vision. While reparametrization-invariant Sobolev metrics provide meaningful elastic distances and point correspondences via the geodesic boundary value problem, solving this problem numerically tends to be difficult. Square root normal fields (SRNF) considerably simplify the computation of certain elastic distances between parametrized surfaces. Yet they leave open the issue of finding optimal reparametrizations, which induce elastic distances between unparametrized surfaces. This issue has concentrated much effort in recent years and led to the development of several numerical frameworks. In this paper, we take an alternative approach which bypasses the direct estimation of reparametrizations: we relax the geodesic boundary constraint using an auxiliary parametrization-blind varifold fidelity metric. This reformulation has several notable benefits. By avoiding altogether the need for reparametrizations, it provides the flexibility to deal with simplicial meshes of arbitrary topologies and sampling patterns. Moreover, the problem lends itself to a coarse-to-fine multi-resolution implementation, which makes the algorithm scalable to large meshes. Furthermore, this approach extends readily to higher-order feature maps such as square root curvature fields and is also able to include surface textures in the matching problem. We demonstrate these advantages on several examples, synthetic and real.