Small Data Explainer -- The impact of small data methods in everyday life

The emergence of breakthrough artificial intelligence (AI) techniques has led to a renewed focus on how small data settings, i.e., settings with limited information, can benefit from such developments. This includes societal issues such as how best to include under-represented groups in data-driven policy and decision making, or the health benefits of assistive technologies such as wearables. We provide a conceptual overview, in particular contrasting small data with big data, and identify common themes from exemplary case studies and application areas. Potential solutions are described in a more detailed technical overview of current data analysis and modelling techniques, highlighting contributions from different disciplines, such as knowledge-driven modelling from statistics and data-driven modelling from computer science. By linking application settings, conceptual contributions and specific techniques, we highlight what is already feasible and suggest what an agenda for fully leveraging small data might look like.

Combining propensity score methods with variational autoencoders for generating synthetic data in presence of latent sub-groups

In settings requiring synthetic data generation based on a clinical cohort, e.g., due to data protection regulations, heterogeneity across individuals might be a nuisance that we need to control or faithfully preserve. The sources of such heterogeneity might be known, e.g., as indicated by sub-groups labels, or might be unknown and thus reflected only in properties of distributions, such as bimodality or skewness. We investigate how such heterogeneity can be preserved and controlled when obtaining synthetic data from variational autoencoders (VAEs), i.e., a generative deep learning technique that utilizes a low-dimensional latent representation. To faithfully reproduce unknown heterogeneity reflected in marginal distributions, we propose to combine VAEs with pre-transformations. For dealing with known heterogeneity due to sub-groups, we complement VAEs with models for group membership, specifically from propensity score regression. The evaluation is performed with a realistic simulation design that features sub-groups and challenging marginal distributions. The proposed approach faithfully recovers the latter, compared to synthetic data approaches that focus purely on marginal distributions. Propensity scores add complementary information, e.g., when visualized in the latent space, and enable sampling of synthetic data with or without sub-group specific characteristics. We also illustrate the proposed approach with real data from an international stroke trial that exhibits considerable distribution differences between study sites, in addition to bimodality. These results indicate that describing heterogeneity by statistical approaches, such as propensity score regression, might be more generally useful for complementing generative deep learning for obtaining synthetic data that faithfully reflects structure from clinical cohorts.

Investigating a domain adaptation approach for integrating different measurement instruments in a longitudinal clinical registry

In a longitudinal clinical registry, different measurement instruments might have been used for assessing individuals at different time points. To combine them, we investigate deep learning techniques for obtaining a joint latent representation, to which the items of different measurement instruments are mapped. This corresponds to domain adaptation, an established concept in computer science for image data. Using the proposed approach as an example, we evaluate the potential of domain adaptation in a longitudinal cohort setting with a rather small number of time points, motivated by an application with different motor function measurement instruments in a registry of spinal muscular atrophy (SMA) patients. There, we model trajectories in the latent representation by ordinary differential equations (ODEs), where person-specific ODE parameters are inferred from baseline characteristics. The goodness of fit and complexity of the ODE solutions then allows to judge the measurement instrument mappings. We subsequently explore how alignment can be improved by incorporating corresponding penalty terms into model fitting. To systematically investigate the effect of differences between measurement instruments, we consider several scenarios based on modified SMA data, including scenarios where a mapping should be feasible in principle and scenarios where no perfect mapping is available. While misalignment increases in more complex scenarios, some structure is still recovered, even if the availability of measurement instruments depends on patient state. A reasonable mapping is feasible also in the more complex real SMA dataset. These results indicate that domain adaptation might be more generally useful in statistical modeling for longitudinal registry data.

A statistical approach to latent dynamic modeling with differential equations

Ordinary differential equations (ODEs) can provide mechanistic models of temporally local changes of processes, where parameters are often informed by external knowledge. While ODEs are popular in systems modeling, they are less established for statistical modeling of longitudinal cohort data, e.g., in a clinical setting. Yet, modeling of local changes could also be attractive for assessing the trajectory of an individual in a cohort in the immediate future given its current status, where ODE parameters could be informed by further characteristics of the individual. However, several hurdles so far limit such use of ODEs, as compared to regression-based function fitting approaches. The potentially higher level of noise in cohort data might be detrimental to ODEs, as the shape of the ODE solution heavily depends on the initial value. In addition, larger numbers of variables multiply such problems and might be difficult to handle for ODEs. To address this, we propose to use each observation in the course of time as the initial value to obtain multiple local ODE solutions and build a combined estimator of the underlying dynamics. Neural networks are used for obtaining a low-dimensional latent space for dynamic modeling from a potentially large number of variables, and for obtaining patient-specific ODE parameters from baseline variables. Simultaneous identification of dynamic models and of a latent space is enabled by recently developed differentiable programming techniques. We illustrate the proposed approach in an application with spinal muscular atrophy patients and a corresponding simulation study. In particular, modeling of local changes in health status at any point in time is contrasted to the interpretation of functions obtained from a global regression. This more generally highlights how different application settings might demand different modeling strategies.

Using Differentiable Programming for Flexible Statistical Modeling

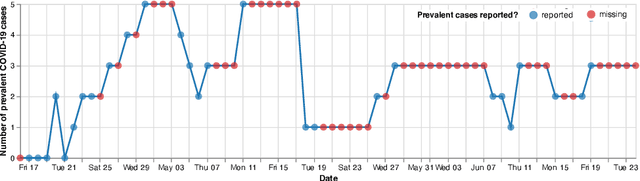
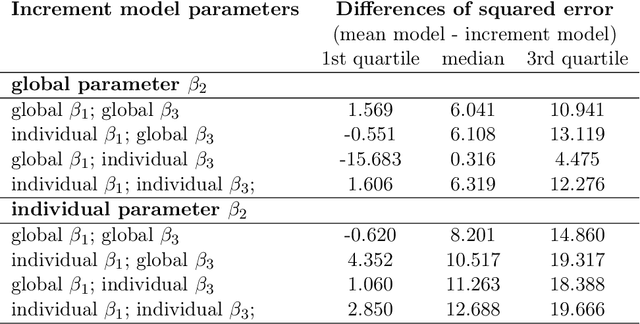
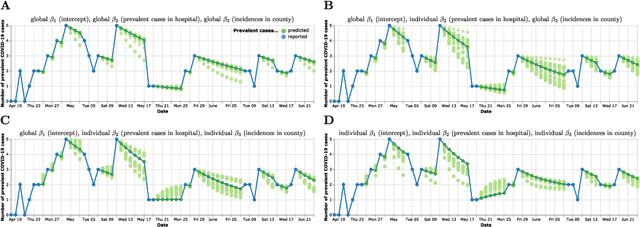
Differentiable programming has recently received much interest as a paradigm that facilitates taking gradients of computer programs. While the corresponding flexible gradient-based optimization approaches so far have been used predominantly for deep learning or enriching the latter with modeling components, we want to demonstrate that they can also be useful for statistical modeling per se, e.g., for quick prototyping when classical maximum likelihood approaches are challenging or not feasible. In an application from a COVID-19 setting, we utilize differentiable programming to quickly build and optimize a flexible prediction model adapted to the data quality challenges at hand. Specifically, we develop a regression model, inspired by delay differential equations, that can bridge temporal gaps of observations in the central German registry of COVID-19 intensive care cases for predicting future demand. With this exemplary modeling challenge, we illustrate how differentiable programming can enable simple gradient-based optimization of the model by automatic differentiation. This allowed us to quickly prototype a model under time pressure that outperforms simpler benchmark models. We thus exemplify the potential of differentiable programming also outside deep learning applications, to provide more options for flexible applied statistical modeling.

Deep dynamic modeling with just two time points: Can we still allow for individual trajectories?

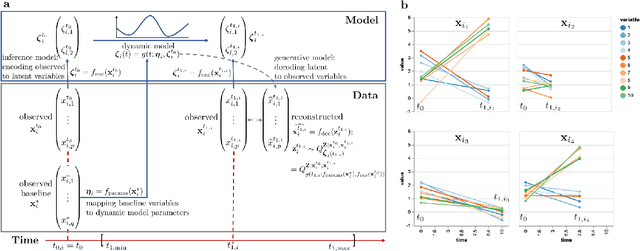
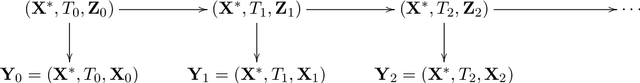
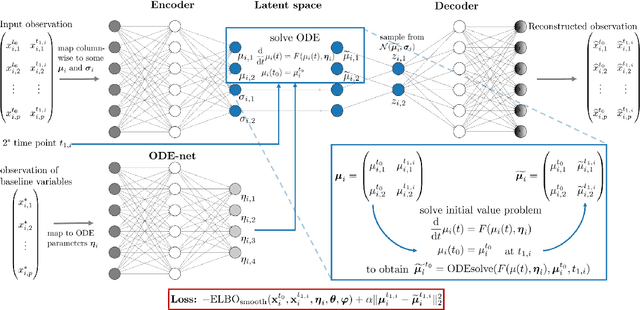
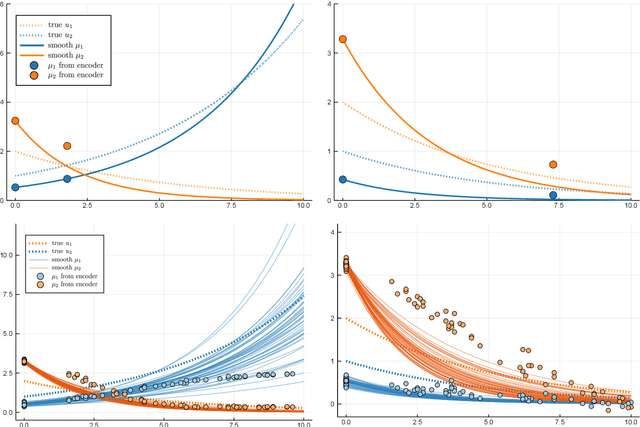
Longitudinal biomedical data are often characterized by a sparse time grid and individual-specific development patterns. Specifically, in epidemiological cohort studies and clinical registries we are facing the question of what can be learned from the data in an early phase of the study, when only a baseline characterization and one follow-up measurement are available. Inspired by recent advances that allow to combine deep learning with dynamic modeling, we investigate whether such approaches can be useful for uncovering complex structure, in particular for an extreme small data setting with only two observations time points for each individual. Irregular spacing in time could then be used to gain more information on individual dynamics by leveraging similarity of individuals. We provide a brief overview of how variational autoencoders (VAEs), as a deep learning approach, can be linked to ordinary differential equations (ODEs) for dynamic modeling, and then specifically investigate the feasibility of such an approach that infers individual-specific latent trajectories by including regularity assumptions and individuals' similarity. We also provide a description of this deep learning approach as a filtering task to give a statistical perspective. Using simulated data, we show to what extent the approach can recover individual trajectories from ODE systems with two and four unknown parameters and infer groups of individuals with similar trajectories, and where it breaks down. The results show that such dynamic deep learning approaches can be useful even in extreme small data settings, but need to be carefully adapted.

The JuliaConnectoR: a functionally oriented interface for integrating Julia in R

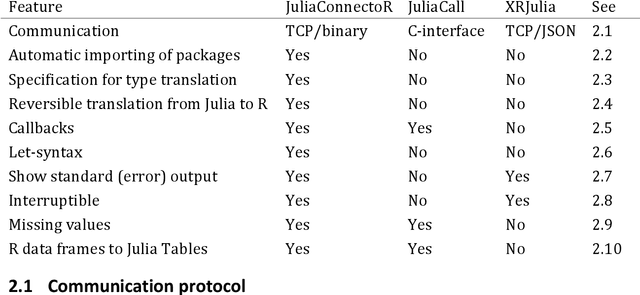
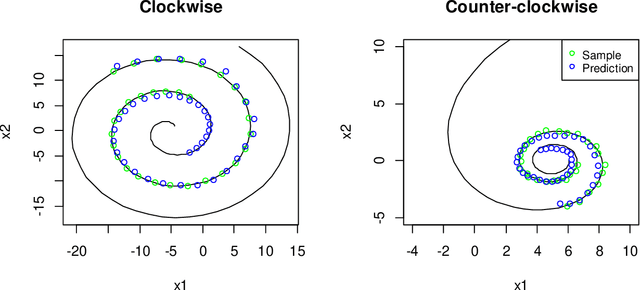
Like many groups considering the new programming language Julia, we faced the challenge of accessing the algorithms that we develop in Julia from R. Therefore, we developed the R package JuliaConnectoR, available from the CRAN repository and GitHub (https://github.com/stefan-m-lenz/JuliaConnectoR), in particular for making advanced deep learning tools available. For maintainability and stability, we decided to base communication between R and Julia on TCP, using an optimized binary format for exchanging data. Our package also specifically contains features that allow for a convenient interactive use in R. This makes it easy to develop R extensions with Julia or to simply call functionality from Julia packages in R. With its functionally oriented design, the JuliaConnectoR enables a clean programming style by avoiding state in Julia that is not visible in the R workspace. We illustrate the further features of our package with code examples, and also discuss advantages over the two alternative packages JuliaCall and XRJulia. Finally, we demonstrate the usage of the package with a more extensive example for employing neural ordinary differential equations, a recent deep learning technique that has received much attention. This example also provides more general guidance for integrating deep learning techniques from Julia into R.