A statistical approach to latent dynamic modeling with differential equations

Ordinary differential equations (ODEs) can provide mechanistic models of temporally local changes of processes, where parameters are often informed by external knowledge. While ODEs are popular in systems modeling, they are less established for statistical modeling of longitudinal cohort data, e.g., in a clinical setting. Yet, modeling of local changes could also be attractive for assessing the trajectory of an individual in a cohort in the immediate future given its current status, where ODE parameters could be informed by further characteristics of the individual. However, several hurdles so far limit such use of ODEs, as compared to regression-based function fitting approaches. The potentially higher level of noise in cohort data might be detrimental to ODEs, as the shape of the ODE solution heavily depends on the initial value. In addition, larger numbers of variables multiply such problems and might be difficult to handle for ODEs. To address this, we propose to use each observation in the course of time as the initial value to obtain multiple local ODE solutions and build a combined estimator of the underlying dynamics. Neural networks are used for obtaining a low-dimensional latent space for dynamic modeling from a potentially large number of variables, and for obtaining patient-specific ODE parameters from baseline variables. Simultaneous identification of dynamic models and of a latent space is enabled by recently developed differentiable programming techniques. We illustrate the proposed approach in an application with spinal muscular atrophy patients and a corresponding simulation study. In particular, modeling of local changes in health status at any point in time is contrasted to the interpretation of functions obtained from a global regression. This more generally highlights how different application settings might demand different modeling strategies.

Using Differentiable Programming for Flexible Statistical Modeling

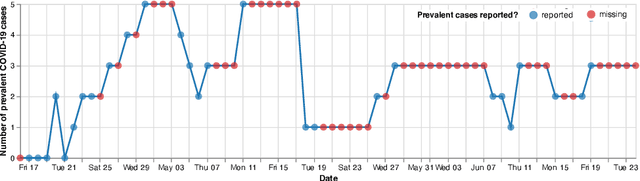
Differentiable programming has recently received much interest as a paradigm that facilitates taking gradients of computer programs. While the corresponding flexible gradient-based optimization approaches so far have been used predominantly for deep learning or enriching the latter with modeling components, we want to demonstrate that they can also be useful for statistical modeling per se, e.g., for quick prototyping when classical maximum likelihood approaches are challenging or not feasible. In an application from a COVID-19 setting, we utilize differentiable programming to quickly build and optimize a flexible prediction model adapted to the data quality challenges at hand. Specifically, we develop a regression model, inspired by delay differential equations, that can bridge temporal gaps of observations in the central German registry of COVID-19 intensive care cases for predicting future demand. With this exemplary modeling challenge, we illustrate how differentiable programming can enable simple gradient-based optimization of the model by automatic differentiation. This allowed us to quickly prototype a model under time pressure that outperforms simpler benchmark models. We thus exemplify the potential of differentiable programming also outside deep learning applications, to provide more options for flexible applied statistical modeling.