Elastic shape analysis of surfaces with second-order Sobolev metrics: a comprehensive numerical framework

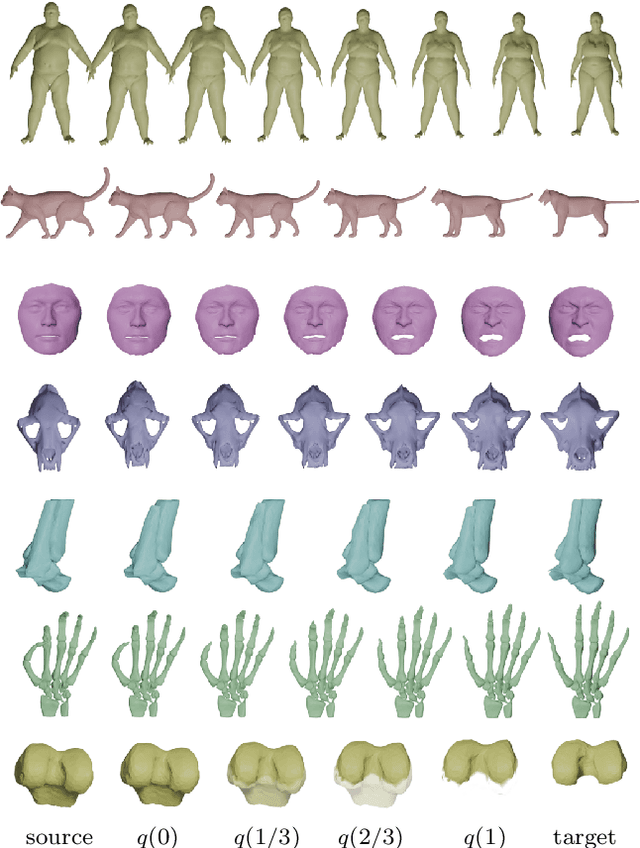
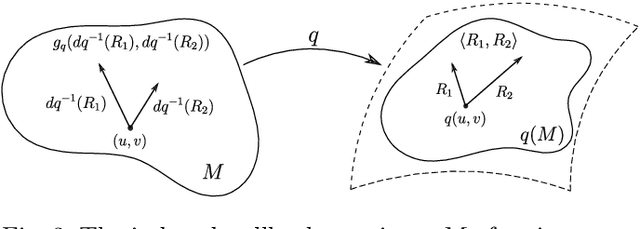
This paper introduces a set of numerical methods for Riemannian shape analysis of 3D surfaces within the setting of invariant (elastic) second-order Sobolev metrics. More specifically, we address the computation of geodesics and geodesic distances between parametrized or unparametrized immersed surfaces represented as 3D meshes. Building on this, we develop tools for the statistical shape analysis of sets of surfaces, including methods for estimating Karcher means and performing tangent PCA on shape populations, and for computing parallel transport along paths of surfaces. Our proposed approach fundamentally relies on a relaxed variational formulation for the geodesic matching problem via the use of varifold fidelity terms, which enable us to enforce reparametrization independence when computing geodesics between unparametrized surfaces, while also yielding versatile algorithms that allow us to compare surfaces with varying sampling or mesh structures. Importantly, we demonstrate how our relaxed variational framework can be extended to tackle partially observed data. The different benefits of our numerical pipeline are illustrated over various examples, synthetic and real.

Supervised deep learning of elastic SRV distances on the shape space of curves

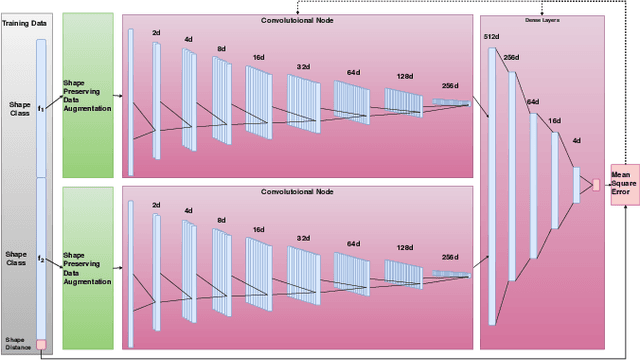
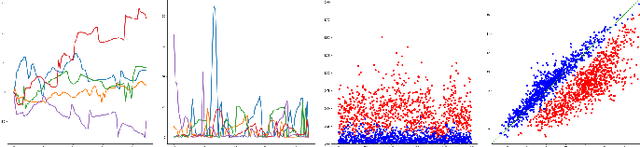
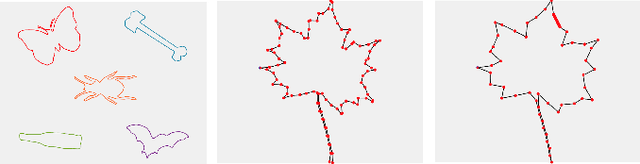
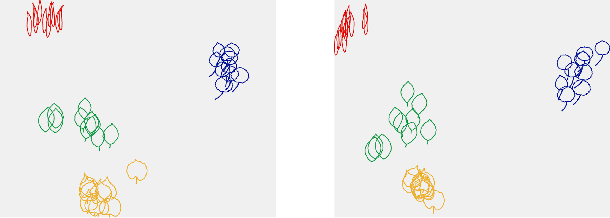
Motivated by applications from computer vision to bioinformatics, the field of shape analysis deals with problems where one wants to analyze geometric objects, such as curves, while ignoring actions that preserve their shape, such as translations, rotations, or reparametrizations. Mathematical tools have been developed to define notions of distances, averages, and optimal deformations for geometric objects. One such framework, which has proven to be successful in many applications, is based on the square root velocity (SRV) transform, which allows one to define a computable distance between spatial curves regardless of how they are parametrized. This paper introduces a supervised deep learning framework for the direct computation of SRV distances between curves, which usually requires an optimization over the group of reparametrizations that act on the curves. The benefits of our approach in terms of computational speed and accuracy are illustrated via several numerical experiments.

Video-Based Action Recognition Using Rate-Invariant Analysis of Covariance Trajectories

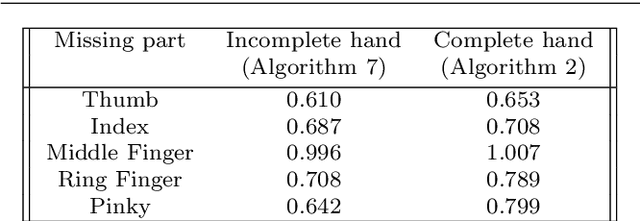
Statistical classification of actions in videos is mostly performed by extracting relevant features, particularly covariance features, from image frames and studying time series associated with temporal evolutions of these features. A natural mathematical representation of activity videos is in form of parameterized trajectories on the covariance manifold, i.e. the set of symmetric, positive-definite matrices (SPDMs). The variable execution-rates of actions implies variable parameterizations of the resulting trajectories, and complicates their classification. Since action classes are invariant to execution rates, one requires rate-invariant metrics for comparing trajectories. A recent paper represented trajectories using their transported square-root vector fields (TSRVFs), defined by parallel translating scaled-velocity vectors of trajectories to a reference tangent space on the manifold. To avoid arbitrariness of selecting the reference and to reduce distortion introduced during this mapping, we develop a purely intrinsic approach where SPDM trajectories are represented by redefining their TSRVFs at the starting points of the trajectories, and analyzed as elements of a vector bundle on the manifold. Using a natural Riemannain metric on vector bundles of SPDMs, we compute geodesic paths and geodesic distances between trajectories in the quotient space of this vector bundle, with respect to the re-parameterization group. This makes the resulting comparison of trajectories invariant to their re-parameterization. We demonstrate this framework on two applications involving video classification: visual speech recognition or lip-reading and hand-gesture recognition. In both cases we achieve results either comparable to or better than the current literature.