Unpaired Volumetric Harmonization of Brain MRI with Conditional Latent Diffusion

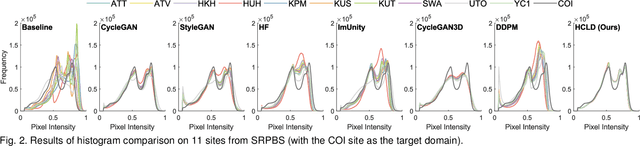
Multi-site structural MRI is increasingly used in neuroimaging studies to diversify subject cohorts. However, combining MR images acquired from various sites/centers may introduce site-related non-biological variations. Retrospective image harmonization helps address this issue, but current methods usually perform harmonization on pre-extracted hand-crafted radiomic features, limiting downstream applicability. Several image-level approaches focus on 2D slices, disregarding inherent volumetric information, leading to suboptimal outcomes. To this end, we propose a novel 3D MRI Harmonization framework through Conditional Latent Diffusion (HCLD) by explicitly considering image style and brain anatomy. It comprises a generalizable 3D autoencoder that encodes and decodes MRIs through a 4D latent space, and a conditional latent diffusion model that learns the latent distribution and generates harmonized MRIs with anatomical information from source MRIs while conditioned on target image style. This enables efficient volume-level MRI harmonization through latent style translation, without requiring paired images from target and source domains during training. The HCLD is trained and evaluated on 4,158 T1-weighted brain MRIs from three datasets in three tasks, assessing its ability to remove site-related variations while retaining essential biological features. Qualitative and quantitative experiments suggest the effectiveness of HCLD over several state-of-the-arts

Learning to Model the Relationship Between Brain Structural and Functional Connectomes

Recent advances in neuroimaging along with algorithmic innovations in statistical learning from network data offer a unique pathway to integrate brain structure and function, and thus facilitate revealing some of the brain's organizing principles at the system level. In this direction, we develop a supervised graph representation learning framework to model the relationship between brain structural connectivity (SC) and functional connectivity (FC) via a graph encoder-decoder system, where the SC is used as input to predict empirical FC. A trainable graph convolutional encoder captures direct and indirect interactions between brain regions-of-interest that mimic actual neural communications, as well as to integrate information from both the structural network topology and nodal (i.e., region-specific) attributes. The encoder learns node-level SC embeddings which are combined to generate (whole brain) graph-level representations for reconstructing empirical FC networks. The proposed end-to-end model utilizes a multi-objective loss function to jointly reconstruct FC networks and learn discriminative graph representations of the SC-to-FC mapping for downstream subject (i.e., graph-level) classification. Comprehensive experiments demonstrate that the learnt representations of said relationship capture valuable information from the intrinsic properties of the subject's brain networks and lead to improved accuracy in classifying a large population of heavy drinkers and non-drinkers from the Human Connectome Project. Our work offers new insights on the relationship between brain networks that support the promising prospect of using graph representation learning to discover more about human brain activity and function.

Amplitude Mean of Functional Data on $\mathbb{S}^2$

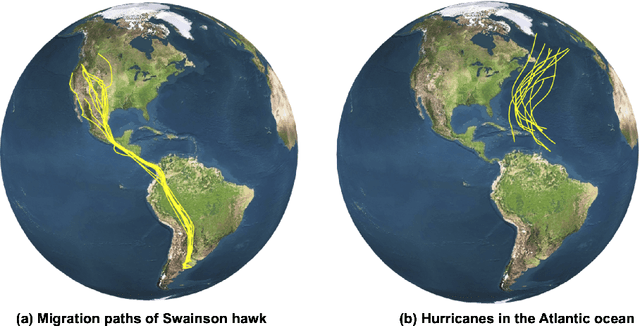
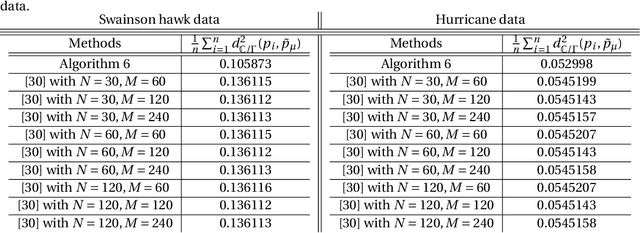
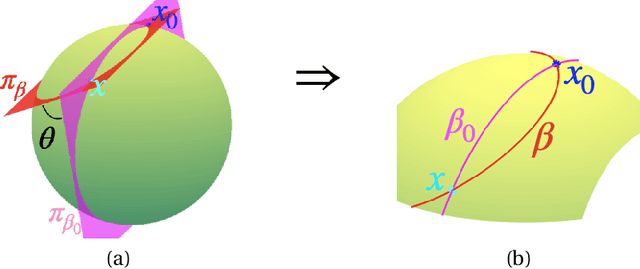
Manifold-valued functional data analysis (FDA) recently becomes an active area of research motivated by the raising availability of trajectories or longitudinal data observed on non-linear manifolds. The challenges of analyzing such data come from many aspects, including infinite dimensionality and nonlinearity, as well as time-domain or phase variability. In this paper, we study the amplitude part of manifold-valued functions on $\mathbb{S}^2$, which is invariant to random time warping or re-parameterization. Utilizing the nice geometry of $\mathbb{S}^2$, we develop a set of efficient and accurate tools for temporal alignment of functions, geodesic computing, and sample mean calculation. At the heart of these tools, they rely on gradient descent algorithms with carefully derived gradients. We show the advantages of these newly developed tools over its competitors with extensive simulations and real data and demonstrate the importance of considering the amplitude part of functions instead of mixing it with phase variability in manifold-valued FDA.

Auto-encoding graph-valued data with applications to brain connectomes

Our interest focuses on developing statistical methods for analysis of brain structural connectomes. Nodes in the brain connectome graph correspond to different regions of interest (ROIs) while edges correspond to white matter fiber connections between these ROIs. Due to the high-dimensionality and non-Euclidean nature of the data, it becomes challenging to conduct analyses of the population distribution of brain connectomes and relate connectomes to other factors, such as cognition. Current approaches focus on summarizing the graph using either pre-specified topological features or principal components analysis (PCA). In this article, we instead develop a nonlinear latent factor model for summarizing the brain graph in both unsupervised and supervised settings. The proposed approach builds on methods for hierarchical modeling of replicated graph data, as well as variational auto-encoders that use neural networks for dimensionality reduction. We refer to our method as Graph AuTo-Encoding (GATE). We compare GATE with tensor PCA and other competitors through simulations and applications to data from the Human Connectome Project (HCP).

Analyzing Dynamical Brain Functional Connectivity As Trajectories on Space of Covariance Matrices

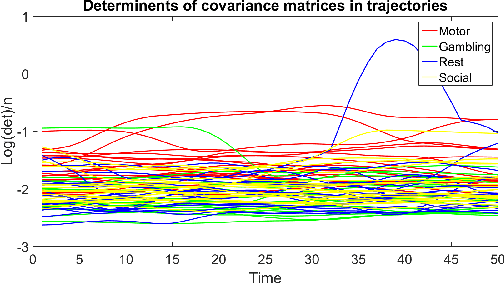
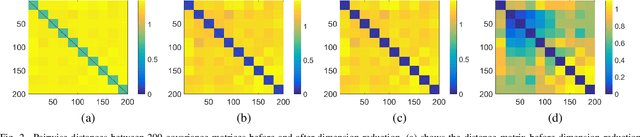
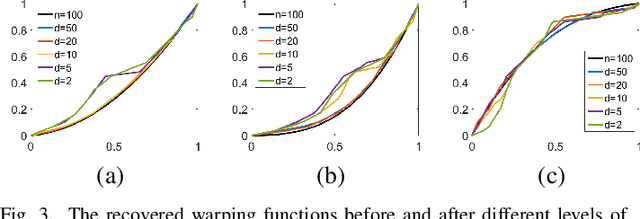
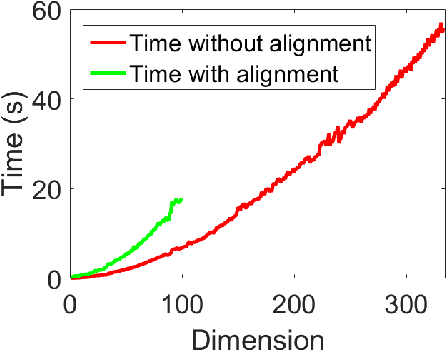
Human brain functional connectivity (FC) is often measured as the similarity of functional MRI responses across brain regions when a brain is either resting or performing a task. This paper aims to statistically analyze the dynamic nature of FC by representing the collective time-series data, over a set of brain regions, as a trajectory on the space of covariance matrices, or symmetric-positive definite matrices (SPDMs). We use a recently developed metric on the space of SPDMs for quantifying differences across FC observations, and for clustering and classification of FC trajectories. To facilitate large scale and high-dimensional data analysis, we propose a novel, metric-based dimensionality reduction technique to reduce data from large SPDMs to small SPDMs. We illustrate this comprehensive framework using data from the Human Connectome Project (HCP) database for multiple subjects and tasks, with task classification rates that match or outperform state-of-the-art techniques.

Discovering Common Change-Point Patterns in Functional Connectivity Across Subjects

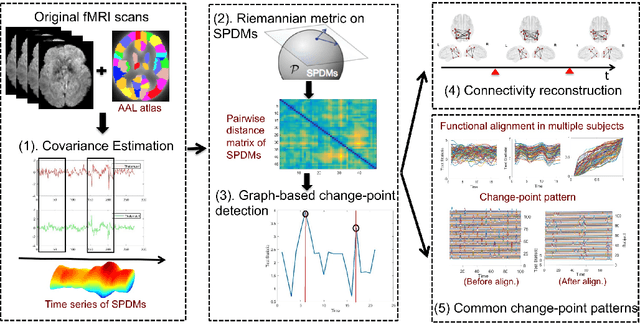
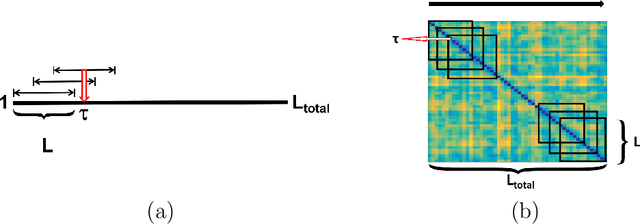
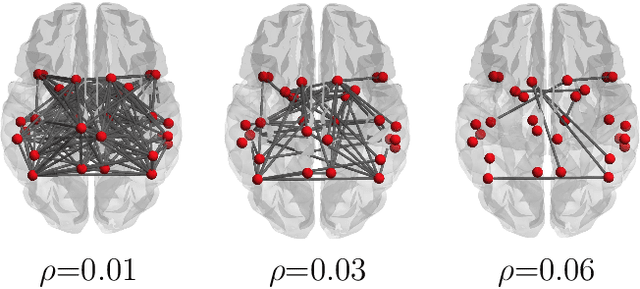
This paper studies change-points in human brain functional connectivity (FC) and seeks patterns that are common across multiple subjects under identical external stimulus. FC relates to the similarity of fMRI responses across different brain regions when the brain is simply resting or performing a task. While the dynamic nature of FC is well accepted, this paper develops a formal statistical test for finding {\it change-points} in times series associated with FC. It represents short-term connectivity by a symmetric positive-definite matrix, and uses a Riemannian metric on this space to develop a graphical method for detecting change-points in a time series of such matrices. It also provides a graphical representation of estimated FC for stationary subintervals in between the detected change-points. Furthermore, it uses a temporal alignment of the test statistic, viewed as a real-valued function over time, to remove inter-subject variability and to discover common change-point patterns across subjects. This method is illustrated using data from Human Connectome Project (HCP) database for multiple subjects and tasks.

Low-Rank Representation over the Manifold of Curves

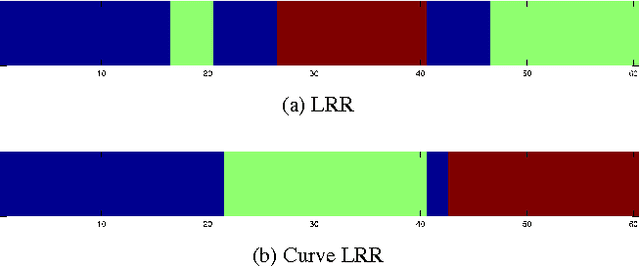
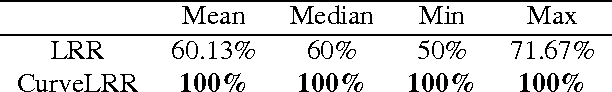
In machine learning it is common to interpret each data point as a vector in Euclidean space. However the data may actually be functional i.e.\ each data point is a function of some variable such as time and the function is discretely sampled. The naive treatment of functional data as traditional multivariate data can lead to poor performance since the algorithms are ignoring the correlation in the curvature of each function. In this paper we propose a method to analyse subspace structure of the functional data by using the state of the art Low-Rank Representation (LRR). Experimental evaluation on synthetic and real data reveals that this method massively outperforms conventional LRR in tasks concerning functional data.

Video-Based Action Recognition Using Rate-Invariant Analysis of Covariance Trajectories

Statistical classification of actions in videos is mostly performed by extracting relevant features, particularly covariance features, from image frames and studying time series associated with temporal evolutions of these features. A natural mathematical representation of activity videos is in form of parameterized trajectories on the covariance manifold, i.e. the set of symmetric, positive-definite matrices (SPDMs). The variable execution-rates of actions implies variable parameterizations of the resulting trajectories, and complicates their classification. Since action classes are invariant to execution rates, one requires rate-invariant metrics for comparing trajectories. A recent paper represented trajectories using their transported square-root vector fields (TSRVFs), defined by parallel translating scaled-velocity vectors of trajectories to a reference tangent space on the manifold. To avoid arbitrariness of selecting the reference and to reduce distortion introduced during this mapping, we develop a purely intrinsic approach where SPDM trajectories are represented by redefining their TSRVFs at the starting points of the trajectories, and analyzed as elements of a vector bundle on the manifold. Using a natural Riemannain metric on vector bundles of SPDMs, we compute geodesic paths and geodesic distances between trajectories in the quotient space of this vector bundle, with respect to the re-parameterization group. This makes the resulting comparison of trajectories invariant to their re-parameterization. We demonstrate this framework on two applications involving video classification: visual speech recognition or lip-reading and hand-gesture recognition. In both cases we achieve results either comparable to or better than the current literature.

Bayesian Clustering of Shapes of Curves

Unsupervised clustering of curves according to their shapes is an important problem with broad scientific applications. The existing model-based clustering techniques either rely on simple probability models (e.g., Gaussian) that are not generally valid for shape analysis or assume the number of clusters. We develop an efficient Bayesian method to cluster curve data using an elastic shape metric that is based on joint registration and comparison of shapes of curves. The elastic-inner product matrix obtained from the data is modeled using a Wishart distribution whose parameters are assigned carefully chosen prior distributions to allow for automatic inference on the number of clusters. Posterior is sampled through an efficient Markov chain Monte Carlo procedure based on the Chinese restaurant process to infer (1) the posterior distribution on the number of clusters, and (2) clustering configuration of shapes. This method is demonstrated on a variety of synthetic data and real data examples on protein structure analysis, cell shape analysis in microscopy images, and clustering of shaped from MPEG7 database.