Constrained Reweighting of Distributions: an Optimal Transport Approach

We commonly encounter the problem of identifying an optimally weight adjusted version of the empirical distribution of observed data, adhering to predefined constraints on the weights. Such constraints often manifest as restrictions on the moments, tail behaviour, shapes, number of modes, etc., of the resulting weight adjusted empirical distribution. In this article, we substantially enhance the flexibility of such methodology by introducing a nonparametrically imbued distributional constraints on the weights, and developing a general framework leveraging the maximum entropy principle and tools from optimal transport. The key idea is to ensure that the maximum entropy weight adjusted empirical distribution of the observed data is close to a pre-specified probability distribution in terms of the optimal transport metric while allowing for subtle departures. The versatility of the framework is demonstrated in the context of three disparate applications where data re-weighting is warranted to satisfy side constraints on the optimization problem at the heart of the statistical task: namely, portfolio allocation, semi-parametric inference for complex surveys, and ensuring algorithmic fairness in machine learning algorithms.

Generalized Regret Analysis of Thompson Sampling using Fractional Posteriors

Thompson sampling (TS) is one of the most popular and earliest algorithms to solve stochastic multi-armed bandit problems. We consider a variant of TS, named $\alpha$-TS, where we use a fractional or $\alpha$-posterior ($\alpha\in(0,1)$) instead of the standard posterior distribution. To compute an $\alpha$-posterior, the likelihood in the definition of the standard posterior is tempered with a factor $\alpha$. For $\alpha$-TS we obtain both instance-dependent $\mathcal{O}\left(\sum_{k \neq i^*} \Delta_k\left(\frac{\log(T)}{C(\alpha)\Delta_k^2} + \frac{1}{2} \right)\right)$ and instance-independent $\mathcal{O}(\sqrt{KT\log K})$ frequentist regret bounds under very mild conditions on the prior and reward distributions, where $\Delta_k$ is the gap between the true mean rewards of the $k^{th}$ and the best arms, and $C(\alpha)$ is a known constant. Both the sub-Gaussian and exponential family models satisfy our general conditions on the reward distribution. Our conditions on the prior distribution just require its density to be positive, continuous, and bounded. We also establish another instance-dependent regret upper bound that matches (up to constants) to that of improved UCB [Auer and Ortner, 2010]. Our regret analysis carefully combines recent theoretical developments in the non-asymptotic concentration analysis and Bernstein-von Mises type results for the $\alpha$-posterior distribution. Moreover, our analysis does not require additional structural properties such as closed-form posteriors or conjugate priors.

Memory Efficient And Minimax Distribution Estimation Under Wasserstein Distance Using Bayesian Histograms

We study Bayesian histograms for distribution estimation on $[0,1]^d$ under the Wasserstein $W_v, 1 \leq v < \infty$ distance in the i.i.d sampling regime. We newly show that when $d < 2v$, histograms possess a special \textit{memory efficiency} property, whereby in reference to the sample size $n$, order $n^{d/2v}$ bins are needed to obtain minimax rate optimality. This result holds for the posterior mean histogram and with respect to posterior contraction: under the class of Borel probability measures and some classes of smooth densities. The attained memory footprint overcomes existing minimax optimal procedures by a polynomial factor in $n$; for example an $n^{1 - d/2v}$ factor reduction in the footprint when compared to the empirical measure, a minimax estimator in the Borel probability measure class. Additionally constructing both the posterior mean histogram and the posterior itself can be done super--linearly in $n$. Due to the popularity of the $W_1,W_2$ metrics and the coverage provided by the $d < 2v$ case, our results are of most practical interest in the $(d=1,v =1,2), (d=2,v=2), (d=3,v=2)$ settings and we provide simulations demonstrating the theory in several of these instances.

On the Convergence of Coordinate Ascent Variational Inference

As a computational alternative to Markov chain Monte Carlo approaches, variational inference (VI) is becoming more and more popular for approximating intractable posterior distributions in large-scale Bayesian models due to its comparable efficacy and superior efficiency. Several recent works provide theoretical justifications of VI by proving its statistical optimality for parameter estimation under various settings; meanwhile, formal analysis on the algorithmic convergence aspects of VI is still largely lacking. In this paper, we consider the common coordinate ascent variational inference (CAVI) algorithm for implementing the mean-field (MF) VI towards optimizing a Kullback--Leibler divergence objective functional over the space of all factorized distributions. Focusing on the two-block case, we analyze the convergence of CAVI by leveraging the extensive toolbox from functional analysis and optimization. We provide general conditions for certifying global or local exponential convergence of CAVI. Specifically, a new notion of generalized correlation for characterizing the interaction between the constituting blocks in influencing the VI objective functional is introduced, which according to the theory, quantifies the algorithmic contraction rate of two-block CAVI. As illustrations, we apply the developed theory to a number of examples, and derive explicit problem-dependent upper bounds on the algorithmic contraction rate.

Fair Clustering via Hierarchical Fair-Dirichlet Process

The advent of ML-driven decision-making and policy formation has led to an increasing focus on algorithmic fairness. As clustering is one of the most commonly used unsupervised machine learning approaches, there has naturally been a proliferation of literature on {\em fair clustering}. A popular notion of fairness in clustering mandates the clusters to be {\em balanced}, i.e., each level of a protected attribute must be approximately equally represented in each cluster. Building upon the original framework, this literature has rapidly expanded in various aspects. In this article, we offer a novel model-based formulation of fair clustering, complementing the existing literature which is almost exclusively based on optimizing appropriate objective functions.

Robust probabilistic inference via a constrained transport metric

Flexible Bayesian models are typically constructed using limits of large parametric models with a multitude of parameters that are often uninterpretable. In this article, we offer a novel alternative by constructing an exponentially tilted empirical likelihood carefully designed to concentrate near a parametric family of distributions of choice with respect to a novel variant of the Wasserstein metric, which is then combined with a prior distribution on model parameters to obtain a robustified posterior. The proposed approach finds applications in a wide variety of robust inference problems, where we intend to perform inference on the parameters associated with the centering distribution in presence of outliers. Our proposed transport metric enjoys great computational simplicity, exploiting the Sinkhorn regularization for discrete optimal transport problems, and being inherently parallelizable. We demonstrate superior performance of our methodology when compared against state-of-the-art robust Bayesian inference methods. We also demonstrate equivalence of our approach with a nonparametric Bayesian formulation under a suitable asymptotic framework, testifying to its flexibility. The constrained entropy maximization that sits at the heart of our likelihood formulation finds its utility beyond robust Bayesian inference; an illustration is provided in a trustworthy machine learning application.

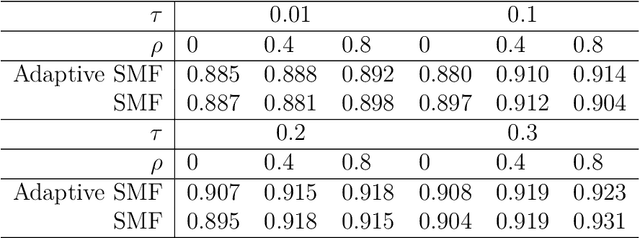
Factorized Fusion Shrinkage for Dynamic Relational Data

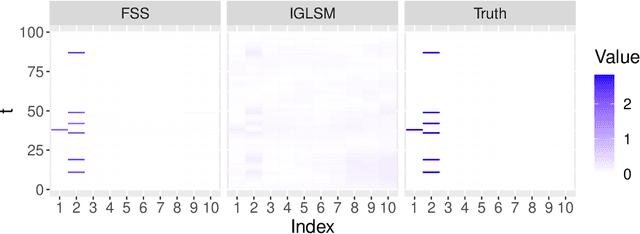
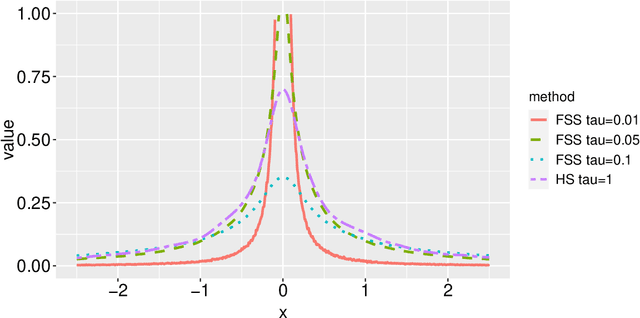
Modern data science applications often involve complex relational data with dynamic structures. An abrupt change in such dynamic relational data is typically observed in systems that undergo regime changes due to interventions. In such a case, we consider a factorized fusion shrinkage model in which all decomposed factors are dynamically shrunk towards group-wise fusion structures, where the shrinkage is obtained by applying global-local shrinkage priors to the successive differences of the row vectors of the factorized matrices. The proposed priors enjoy many favorable properties in comparison and clustering of the estimated dynamic latent factors. Comparing estimated latent factors involves both adjacent and long-term comparisons, with the time range of comparison considered as a variable. Under certain conditions, we demonstrate that the posterior distribution attains the minimax optimal rate up to logarithmic factors. In terms of computation, we present a structured mean-field variational inference framework that balances optimal posterior inference with computational scalability, exploiting both the dependence among components and across time. The framework can accommodate a wide variety of models, including dynamic matrix factorization, latent space models for networks and low-rank tensors. The effectiveness of our methodology is demonstrated through extensive simulations and real-world data analysis.

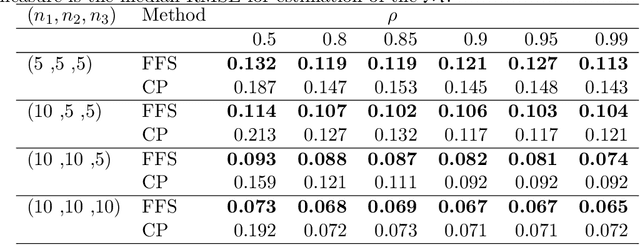
Structured Optimal Variational Inference for Dynamic Latent Space Models

We consider a latent space model for dynamic networks, where our objective is to estimate the pairwise inner products of the latent positions. To balance posterior inference and computational scalability, we present a structured mean-field variational inference framework, where the time-dependent properties of the dynamic networks are exploited to facilitate computation and inference. Additionally, an easy-to-implement block coordinate ascent algorithm is developed with message-passing type updates in each block, whereas the complexity per iteration is linear with the number of nodes and time points. To facilitate learning of the pairwise latent distances, we adopt a Gamma prior for the transition variance different from the literature. To certify the optimality, we demonstrate that the variational risk of the proposed variational inference approach attains the minimax optimal rate under certain conditions. En route, we derive the minimax lower bound, which might be of independent interest. To best of our knowledge, this is the first such exercise for dynamic latent space models. Simulations and real data analysis demonstrate the efficacy of our methodology and the efficiency of our algorithm. Finally, our proposed methodology can be readily extended to the case where the scales of the latent nodes are learned in a nodewise manner.

Off-Policy Evaluation Using Information Borrowing and Context-Based Switching

We consider the off-policy evaluation (OPE) problem in contextual bandits, where the goal is to estimate the value of a target policy using the data collected by a logging policy. Most popular approaches to the OPE are variants of the doubly robust (DR) estimator obtained by combining a direct method (DM) estimator and a correction term involving the inverse propensity score (IPS). Existing algorithms primarily focus on strategies to reduce the variance of the DR estimator arising from large IPS. We propose a new approach called the Doubly Robust with Information borrowing and Context-based switching (DR-IC) estimator that focuses on reducing both bias and variance. The DR-IC estimator replaces the standard DM estimator with a parametric reward model that borrows information from the 'closer' contexts through a correlation structure that depends on the IPS. The DR-IC estimator also adaptively interpolates between this modified DM estimator and a modified DR estimator based on a context-specific switching rule. We give provable guarantees on the performance of the DR-IC estimator. We also demonstrate the superior performance of the DR-IC estimator compared to the state-of-the-art OPE algorithms on a number of benchmark problems.

Statistical Guarantees for Transformation Based Models with Applications to Implicit Variational Inference

Transformation-based methods have been an attractive approach in non-parametric inference for problems such as unconditional and conditional density estimation due to their unique hierarchical structure that models the data as flexible transformation of a set of common latent variables. More recently, transformation-based models have been used in variational inference (VI) to construct flexible implicit families of variational distributions. However, their use in both non-parametric inference and variational inference lacks theoretical justification. We provide theoretical justification for the use of non-linear latent variable models (NL-LVMs) in non-parametric inference by showing that the support of the transformation induced prior in the space of densities is sufficiently large in the $L_1$ sense. We also show that, when a Gaussian process (GP) prior is placed on the transformation function, the posterior concentrates at the optimal rate up to a logarithmic factor. Adopting the flexibility demonstrated in the non-parametric setting, we use the NL-LVM to construct an implicit family of variational distributions, deemed GP-IVI. We delineate sufficient conditions under which GP-IVI achieves optimal risk bounds and approximates the true posterior in the sense of the Kullback-Leibler divergence. To the best of our knowledge, this is the first work on providing theoretical guarantees for implicit variational inference.