A unified Bayesian framework for interval hypothesis testing in clinical trials

The American Statistical Association (ASA) statement on statistical significance and P-values \cite{wasserstein2016asa} cautioned statisticians against making scientific decisions solely on the basis of traditional P-values. The statement delineated key issues with P-values, including a lack of transparency, an inability to quantify evidence in support of the null hypothesis, and an inability to measure the size of an effect or the importance of a result. In this article, we demonstrate that the interval null hypothesis framework (instead of the point null hypothesis framework), when used in tandem with Bayes factor-based tests, is instrumental in circumnavigating the key issues of P-values. Further, we note that specifying prior densities for Bayes factors is challenging and has been a reason for criticism of Bayesian hypothesis testing in existing literature. We address this by adapting Bayes factors directly based on common test statistics. We demonstrate, through numerical experiments and real data examples, that the proposed Bayesian interval hypothesis testing procedures can be calibrated to ensure frequentist error control while retaining their inherent interpretability. Finally, we illustrate the improved flexibility and applicability of the proposed methods by providing coherent frameworks for competitive landscape analysis and end-to-end Bayesian hypothesis tests in the context of reporting clinical trial outcomes.

Differentially Private Bayesian Tests

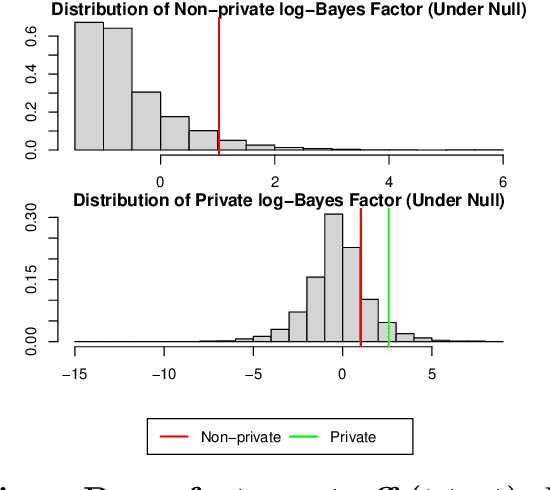
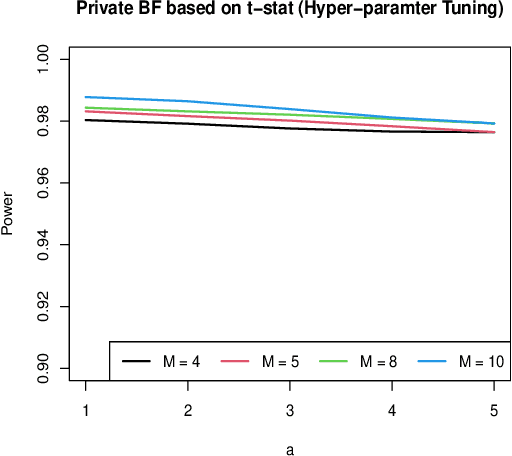
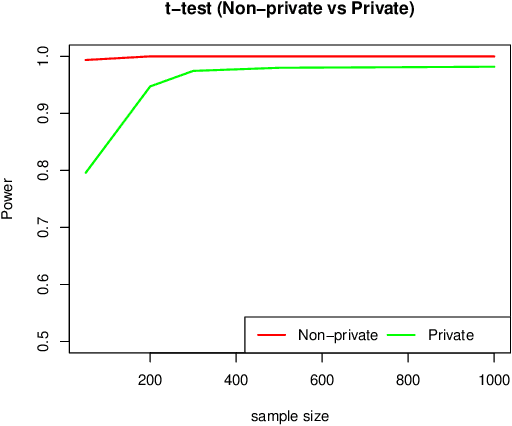
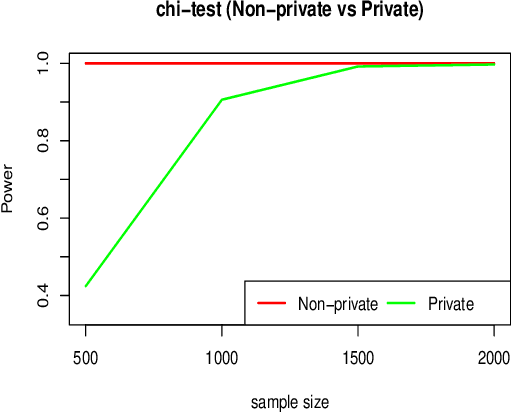
Differential privacy has emerged as an significant cornerstone in the realm of scientific hypothesis testing utilizing confidential data. In reporting scientific discoveries, Bayesian tests are widely adopted since they effectively circumnavigate the key criticisms of P-values, namely, lack of interpretability and inability to quantify evidence in support of the competing hypotheses. We present a novel differentially private Bayesian hypotheses testing framework that arise naturally under a principled data generative mechanism, inherently maintaining the interpretability of the resulting inferences. Furthermore, by focusing on differentially private Bayes factors based on widely used test statistics, we circumvent the need to model the complete data generative mechanism and ensure substantial computational benefits. We also provide a set of sufficient conditions to establish results on Bayes factor consistency under the proposed framework. The utility of the devised technology is showcased via several numerical experiments.

Constrained Reweighting of Distributions: an Optimal Transport Approach

We commonly encounter the problem of identifying an optimally weight adjusted version of the empirical distribution of observed data, adhering to predefined constraints on the weights. Such constraints often manifest as restrictions on the moments, tail behaviour, shapes, number of modes, etc., of the resulting weight adjusted empirical distribution. In this article, we substantially enhance the flexibility of such methodology by introducing a nonparametrically imbued distributional constraints on the weights, and developing a general framework leveraging the maximum entropy principle and tools from optimal transport. The key idea is to ensure that the maximum entropy weight adjusted empirical distribution of the observed data is close to a pre-specified probability distribution in terms of the optimal transport metric while allowing for subtle departures. The versatility of the framework is demonstrated in the context of three disparate applications where data re-weighting is warranted to satisfy side constraints on the optimization problem at the heart of the statistical task: namely, portfolio allocation, semi-parametric inference for complex surveys, and ensuring algorithmic fairness in machine learning algorithms.

Scalable Model-Based Gaussian Process Clustering

Gaussian process is an indispensable tool in clustering functional data, owing to it's flexibility and inherent uncertainty quantification. However, when the functional data is observed over a large grid (say, of length $p$), Gaussian process clustering quickly renders itself infeasible, incurring $O(p^2)$ space complexity and $O(p^3)$ time complexity per iteration; and thus prohibiting it's natural adaptation to large environmental applications. To ensure scalability of Gaussian process clustering in such applications, we propose to embed the popular Vecchia approximation for Gaussian processes at the heart of the clustering task, provide crucial theoretical insights towards algorithmic design, and finally develop a computationally efficient expectation maximization (EM) algorithm. Empirical evidence of the utility of our proposal is provided via simulations and analysis of polar temperature anomaly (\href{https://www.ncei.noaa.gov/access/monitoring/climate-at-a-glance/global/time-series}{noaa.gov}) data-sets.

Fair Clustering via Hierarchical Fair-Dirichlet Process

The advent of ML-driven decision-making and policy formation has led to an increasing focus on algorithmic fairness. As clustering is one of the most commonly used unsupervised machine learning approaches, there has naturally been a proliferation of literature on {\em fair clustering}. A popular notion of fairness in clustering mandates the clusters to be {\em balanced}, i.e., each level of a protected attribute must be approximately equally represented in each cluster. Building upon the original framework, this literature has rapidly expanded in various aspects. In this article, we offer a novel model-based formulation of fair clustering, complementing the existing literature which is almost exclusively based on optimizing appropriate objective functions.

Robust probabilistic inference via a constrained transport metric

Flexible Bayesian models are typically constructed using limits of large parametric models with a multitude of parameters that are often uninterpretable. In this article, we offer a novel alternative by constructing an exponentially tilted empirical likelihood carefully designed to concentrate near a parametric family of distributions of choice with respect to a novel variant of the Wasserstein metric, which is then combined with a prior distribution on model parameters to obtain a robustified posterior. The proposed approach finds applications in a wide variety of robust inference problems, where we intend to perform inference on the parameters associated with the centering distribution in presence of outliers. Our proposed transport metric enjoys great computational simplicity, exploiting the Sinkhorn regularization for discrete optimal transport problems, and being inherently parallelizable. We demonstrate superior performance of our methodology when compared against state-of-the-art robust Bayesian inference methods. We also demonstrate equivalence of our approach with a nonparametric Bayesian formulation under a suitable asymptotic framework, testifying to its flexibility. The constrained entropy maximization that sits at the heart of our likelihood formulation finds its utility beyond robust Bayesian inference; an illustration is provided in a trustworthy machine learning application.