Doubly Robust Fusion of Many Treatments for Policy Learning

Individualized treatment rules/recommendations (ITRs) aim to improve patient outcomes by tailoring treatments to the characteristics of each individual. However, when there are many treatment groups, existing methods face significant challenges due to data sparsity within treatment groups and highly unbalanced covariate distributions across groups. To address these challenges, we propose a novel calibration-weighted treatment fusion procedure that robustly balances covariates across treatment groups and fuses similar treatments using a penalized working model. The fusion procedure ensures the recovery of latent treatment group structures when either the calibration model or the outcome model is correctly specified. In the fused treatment space, practitioners can seamlessly apply state-of-the-art ITR learning methods with the flexibility to utilize a subset of covariates, thereby achieving robustness while addressing practical concerns such as fairness. We establish theoretical guarantees, including consistency, the oracle property of treatment fusion, and regret bounds when integrated with multi-armed ITR learning methods such as policy trees. Simulation studies show superior group recovery and policy value compared to existing approaches. We illustrate the practical utility of our method using a nationwide electronic health record-derived de-identified database containing data from patients with Chronic Lymphocytic Leukemia and Small Lymphocytic Lymphoma.

Overview and practical recommendations on using Shapley Values for identifying predictive biomarkers via CATE modeling

In recent years, two parallel research trends have emerged in machine learning, yet their intersections remain largely unexplored. On one hand, there has been a significant increase in literature focused on Individual Treatment Effect (ITE) modeling, particularly targeting the Conditional Average Treatment Effect (CATE) using meta-learner techniques. These approaches often aim to identify causal effects from observational data. On the other hand, the field of Explainable Machine Learning (XML) has gained traction, with various approaches developed to explain complex models and make their predictions more interpretable. A prominent technique in this area is Shapley Additive Explanations (SHAP), which has become mainstream in data science for analyzing supervised learning models. However, there has been limited exploration of SHAP application in identifying predictive biomarkers through CATE models, a crucial aspect in pharmaceutical precision medicine. We address inherent challenges associated with the SHAP concept in multi-stage CATE strategies and introduce a surrogate estimation approach that is agnostic to the choice of CATE strategy, effectively reducing computational burdens in high-dimensional data. Using this approach, we conduct simulation benchmarking to evaluate the ability to accurately identify biomarkers using SHAP values derived from various CATE meta-learners and Causal Forest.

A unified Bayesian framework for interval hypothesis testing in clinical trials

The American Statistical Association (ASA) statement on statistical significance and P-values \cite{wasserstein2016asa} cautioned statisticians against making scientific decisions solely on the basis of traditional P-values. The statement delineated key issues with P-values, including a lack of transparency, an inability to quantify evidence in support of the null hypothesis, and an inability to measure the size of an effect or the importance of a result. In this article, we demonstrate that the interval null hypothesis framework (instead of the point null hypothesis framework), when used in tandem with Bayes factor-based tests, is instrumental in circumnavigating the key issues of P-values. Further, we note that specifying prior densities for Bayes factors is challenging and has been a reason for criticism of Bayesian hypothesis testing in existing literature. We address this by adapting Bayes factors directly based on common test statistics. We demonstrate, through numerical experiments and real data examples, that the proposed Bayesian interval hypothesis testing procedures can be calibrated to ensure frequentist error control while retaining their inherent interpretability. Finally, we illustrate the improved flexibility and applicability of the proposed methods by providing coherent frameworks for competitive landscape analysis and end-to-end Bayesian hypothesis tests in the context of reporting clinical trial outcomes.

When Doubly Robust Methods Meet Machine Learning for Estimating Treatment Effects from Real-World Data: A Comparative Study

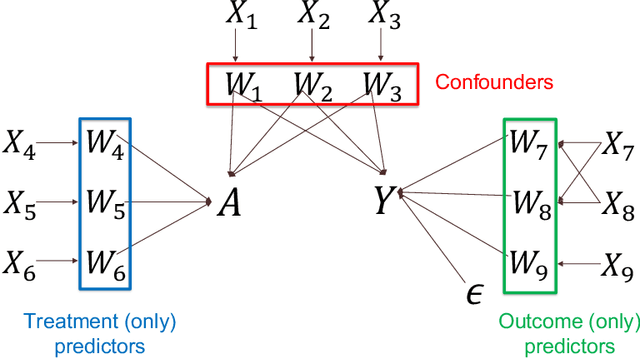
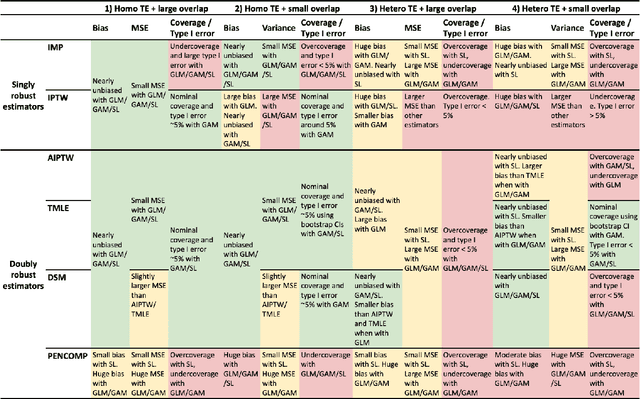
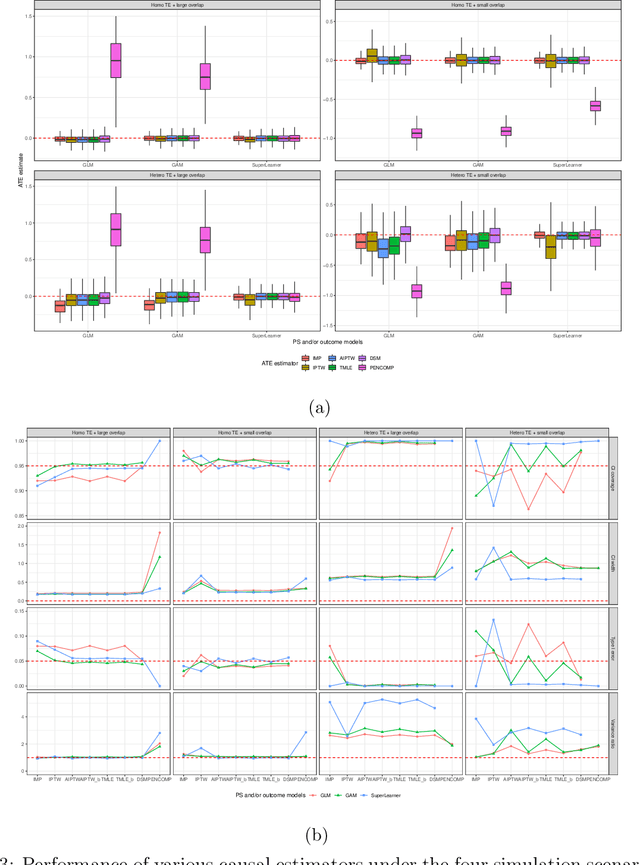
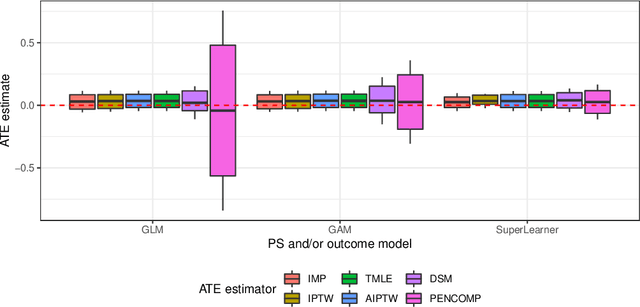
Observational cohort studies are increasingly being used for comparative effectiveness research and to assess the safety of therapeutics. Recently, various doubly robust methods have been proposed for average treatment effect estimation by combining the treatment model and the outcome model via different vehicles, such as matching, weighting, and regression. The key advantage of the doubly robust estimators is that they require either the treatment model or the outcome model to be correctly specified to obtain a consistent estimator of the average treatment effect, and therefore lead to a more accurate and often more precise inference. However, little work has been done to understand how doubly robust estimators differ due to their unique strategies of using the treatment and outcome models and how machine learning techniques can be combined with these estimators to boost their performance. Also, little has been understood about the challenges of covariates selection, overlapping of the covariate distribution, and treatment effect heterogeneity on the performance of these doubly robust estimators. Here we examine multiple popular doubly robust methods in the categories of matching, weighting, or regression, and compare their performance using different treatment and outcome modeling via extensive simulations and a real-world application. We found that incorporating machine learning with doubly robust estimators such as the targeted maximum likelihood estimator outperforms. Practical guidance on how to apply doubly robust estimators is provided.