Overview and practical recommendations on using Shapley Values for identifying predictive biomarkers via CATE modeling

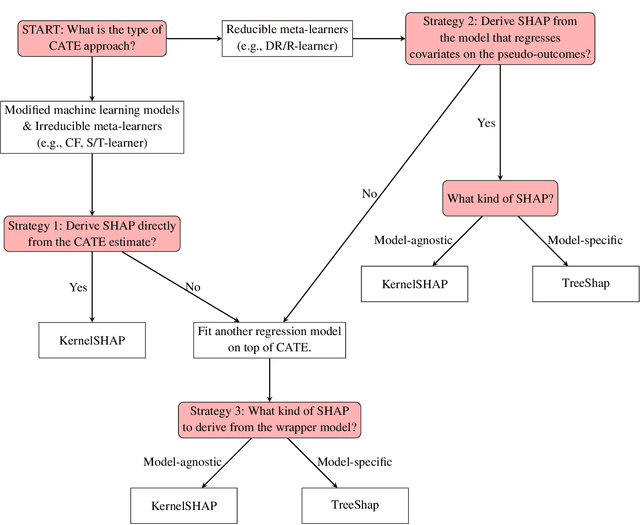
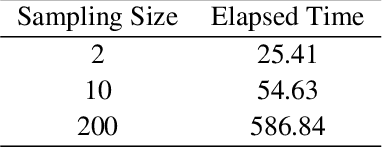
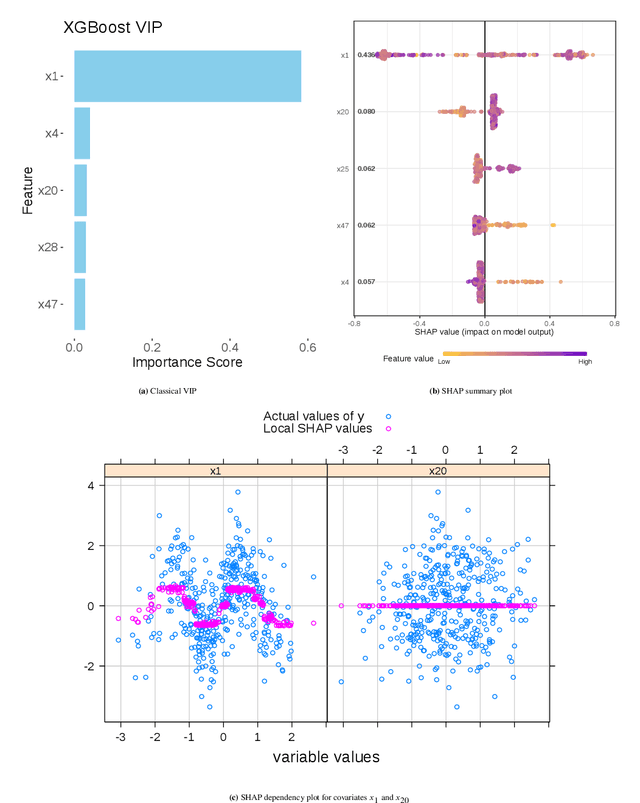
In recent years, two parallel research trends have emerged in machine learning, yet their intersections remain largely unexplored. On one hand, there has been a significant increase in literature focused on Individual Treatment Effect (ITE) modeling, particularly targeting the Conditional Average Treatment Effect (CATE) using meta-learner techniques. These approaches often aim to identify causal effects from observational data. On the other hand, the field of Explainable Machine Learning (XML) has gained traction, with various approaches developed to explain complex models and make their predictions more interpretable. A prominent technique in this area is Shapley Additive Explanations (SHAP), which has become mainstream in data science for analyzing supervised learning models. However, there has been limited exploration of SHAP application in identifying predictive biomarkers through CATE models, a crucial aspect in pharmaceutical precision medicine. We address inherent challenges associated with the SHAP concept in multi-stage CATE strategies and introduce a surrogate estimation approach that is agnostic to the choice of CATE strategy, effectively reducing computational burdens in high-dimensional data. Using this approach, we conduct simulation benchmarking to evaluate the ability to accurately identify biomarkers using SHAP values derived from various CATE meta-learners and Causal Forest.

Inferring Causal Direction from Observational Data: A Complexity Approach

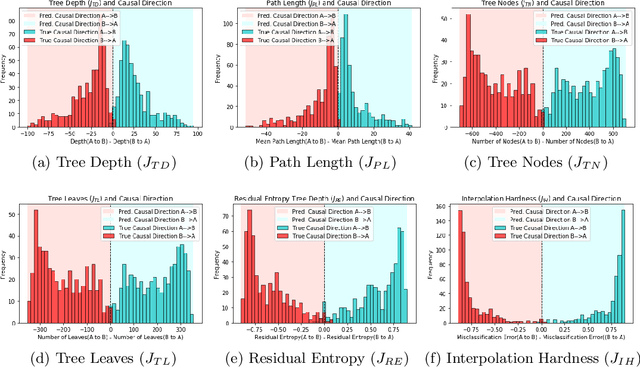
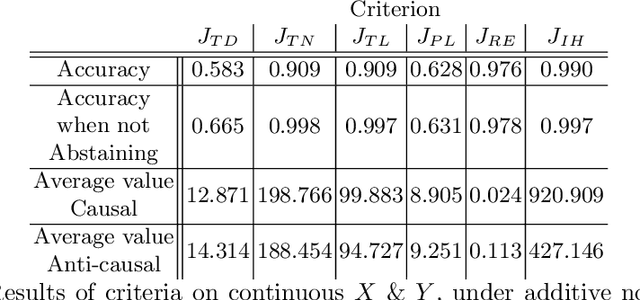
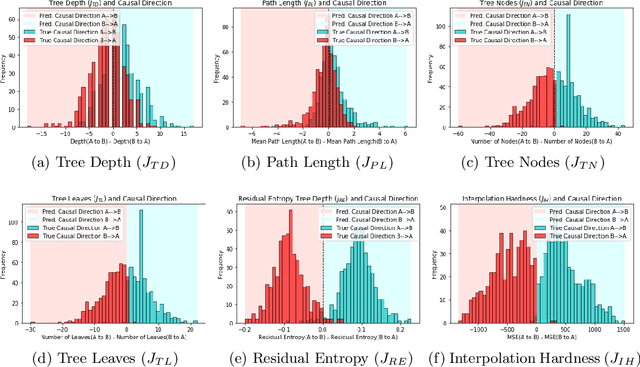
At the heart of causal structure learning from observational data lies a deceivingly simple question: given two statistically dependent random variables, which one has a causal effect on the other? This is impossible to answer using statistical dependence testing alone and requires that we make additional assumptions. We propose several fast and simple criteria for distinguishing cause and effect in pairs of discrete or continuous random variables. The intuition behind them is that predicting the effect variable using the cause variable should be `simpler' than the reverse -- different notions of `simplicity' giving rise to different criteria. We demonstrate the accuracy of the criteria on synthetic data generated under a broad family of causal mechanisms and types of noise.

Multi-target regression via output space quantization

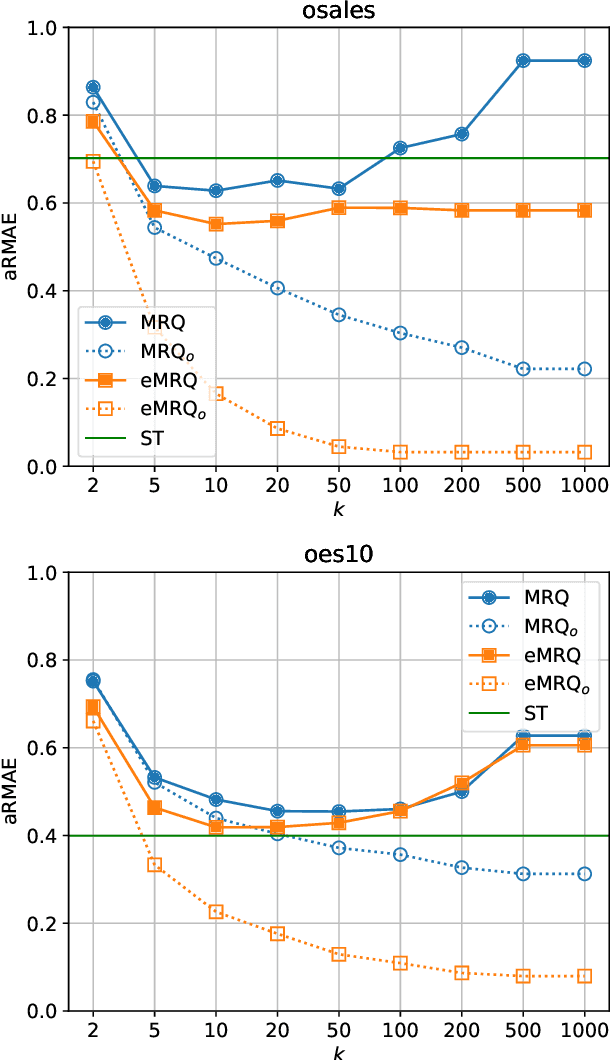
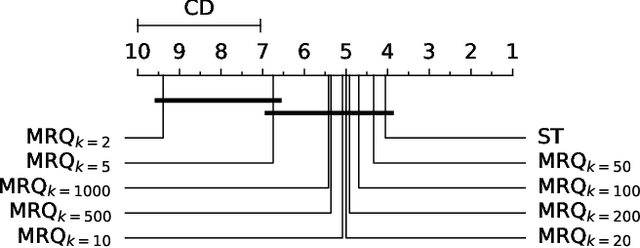
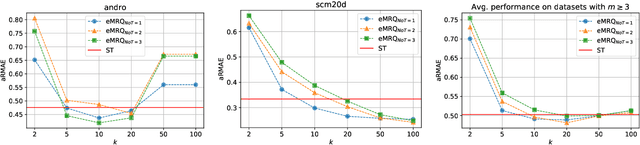
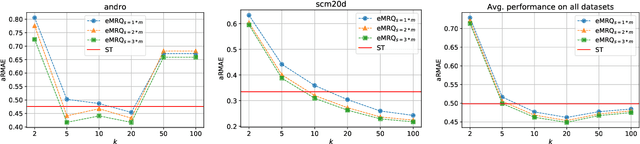
Multi-target regression is concerned with the prediction of multiple continuous target variables using a shared set of predictors. Two key challenges in multi-target regression are: (a) modelling target dependencies and (b) scalability to large output spaces. In this paper, a new multi-target regression method is proposed that tries to jointly address these challenges via a novel problem transformation approach. The proposed method, called MRQ, is based on the idea of quantizing the output space in order to transform the multiple continuous targets into one or more discrete ones. Learning on the transformed output space naturally enables modeling of target dependencies while the quantization strategy can be flexibly parameterized to control the trade-off between prediction accuracy and computational efficiency. Experiments on a large collection of benchmark datasets show that MRQ is both highly scalable and also competitive with the state-of-the-art in terms of accuracy. In particular, an ensemble version of MRQ obtains the best overall accuracy, while being an order of magnitude faster than the runner up method.

Ranking Biomarkers Through Mutual Information

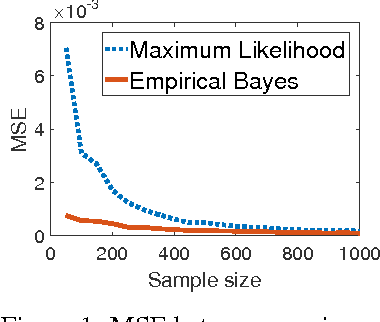
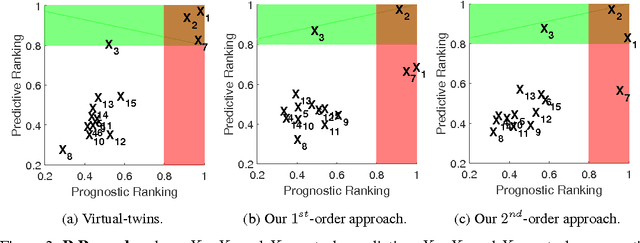
We study information theoretic methods for ranking biomarkers. In clinical trials there are two, closely related, types of biomarkers: predictive and prognostic, and disentangling them is a key challenge. Our first step is to phrase biomarker ranking in terms of optimizing an information theoretic quantity. This formalization of the problem will enable us to derive rankings of predictive/prognostic biomarkers, by estimating different, high dimensional, conditional mutual information terms. To estimate these terms, we suggest efficient low dimensional approximations, and we derive an empirical Bayes estimator, which is suitable for small or sparse datasets. Finally, we introduce a new visualisation tool that captures the prognostic and the predictive strength of a set of biomarkers. We believe this representation will prove to be a powerful tool in biomarker discovery.