Deconfounded Warm-Start Thompson Sampling with Applications to Precision Medicine

Randomized clinical trials often require large patient cohorts before drawing definitive conclusions, yet abundant observational data from parallel studies remains underutilized due to confounding and hidden biases. To bridge this gap, we propose Deconfounded Warm-Start Thompson Sampling (DWTS), a practical approach that leverages a Doubly Debiased LASSO (DDL) procedure to identify a sparse set of reliable measured covariates and combines them with key hidden covariates to form a reduced context. By initializing Thompson Sampling (LinTS) priors with DDL-estimated means and variances on these measured features -- while keeping uninformative priors on hidden features -- DWTS effectively harnesses confounded observational data to kick-start adaptive clinical trials. Evaluated on both a purely synthetic environment and a virtual environment created using real cardiovascular risk dataset, DWTS consistently achieves lower cumulative regret than standard LinTS, showing how offline causal insights from observational data can improve trial efficiency and support more personalized treatment decisions.

Generalized Regret Analysis of Thompson Sampling using Fractional Posteriors

Thompson sampling (TS) is one of the most popular and earliest algorithms to solve stochastic multi-armed bandit problems. We consider a variant of TS, named $\alpha$-TS, where we use a fractional or $\alpha$-posterior ($\alpha\in(0,1)$) instead of the standard posterior distribution. To compute an $\alpha$-posterior, the likelihood in the definition of the standard posterior is tempered with a factor $\alpha$. For $\alpha$-TS we obtain both instance-dependent $\mathcal{O}\left(\sum_{k \neq i^*} \Delta_k\left(\frac{\log(T)}{C(\alpha)\Delta_k^2} + \frac{1}{2} \right)\right)$ and instance-independent $\mathcal{O}(\sqrt{KT\log K})$ frequentist regret bounds under very mild conditions on the prior and reward distributions, where $\Delta_k$ is the gap between the true mean rewards of the $k^{th}$ and the best arms, and $C(\alpha)$ is a known constant. Both the sub-Gaussian and exponential family models satisfy our general conditions on the reward distribution. Our conditions on the prior distribution just require its density to be positive, continuous, and bounded. We also establish another instance-dependent regret upper bound that matches (up to constants) to that of improved UCB [Auer and Ortner, 2010]. Our regret analysis carefully combines recent theoretical developments in the non-asymptotic concentration analysis and Bernstein-von Mises type results for the $\alpha$-posterior distribution. Moreover, our analysis does not require additional structural properties such as closed-form posteriors or conjugate priors.

Facial De-morphing: Extracting Component Faces from a Single Morph

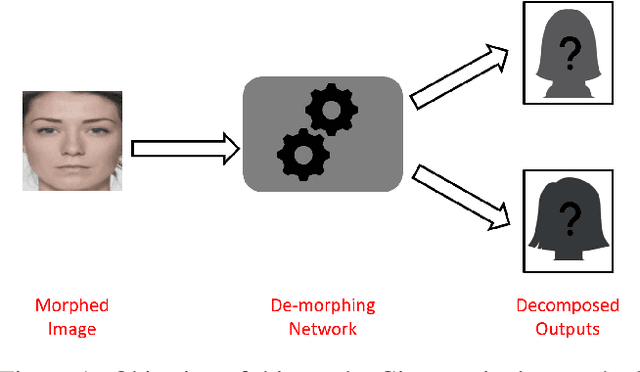
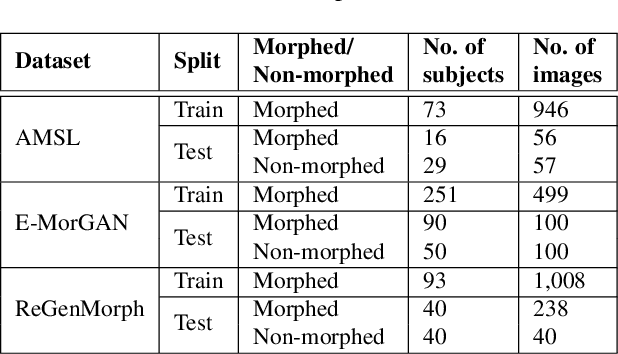
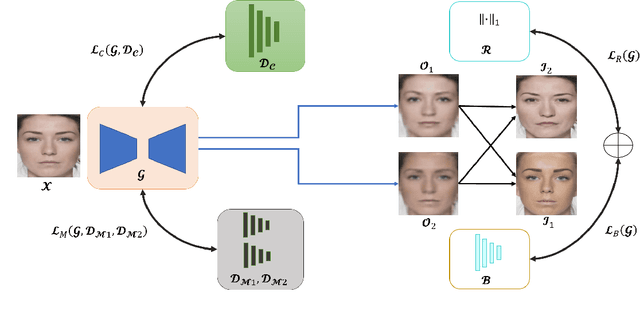
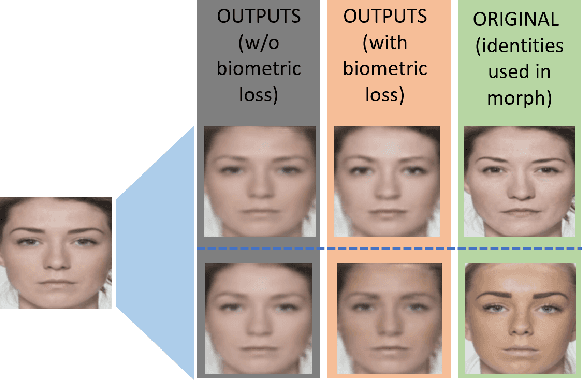
A face morph is created by strategically combining two or more face images corresponding to multiple identities. The intention is for the morphed image to match with multiple identities. Current morph attack detection strategies can detect morphs but cannot recover the images or identities used in creating them. The task of deducing the individual face images from a morphed face image is known as \textit{de-morphing}. Existing work in de-morphing assume the availability of a reference image pertaining to one identity in order to recover the image of the accomplice - i.e., the other identity. In this work, we propose a novel de-morphing method that can recover images of both identities simultaneously from a single morphed face image without needing a reference image or prior information about the morphing process. We propose a generative adversarial network that achieves single image-based de-morphing with a surprisingly high degree of visual realism and biometric similarity with the original face images. We demonstrate the performance of our method on landmark-based morphs and generative model-based morphs with promising results.

Bayesian Joint Chance Constrained Optimization: Approximations and Statistical Consistency

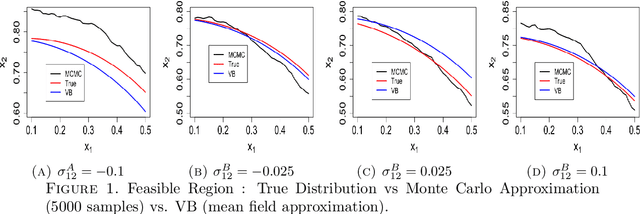
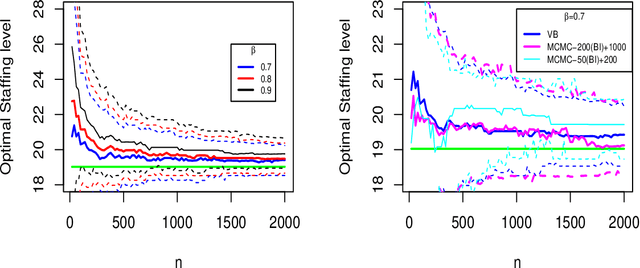
This paper considers data-driven chance-constrained stochastic optimization problems in a Bayesian framework. Bayesian posteriors afford a principled mechanism to incorporate data and prior knowledge into stochastic optimization problems. However, the computation of Bayesian posteriors is typically an intractable problem, and has spawned a large literature on approximate Bayesian computation. Here, in the context of chance-constrained optimization, we focus on the question of statistical consistency (in an appropriate sense) of the optimal value, computed using an approximate posterior distribution. To this end, we rigorously prove a frequentist consistency result demonstrating the convergence of the optimal value to the optimal value of a fixed, parameterized constrained optimization problem. We augment this by also establishing a probabilistic rate of convergence of the optimal value. We also prove the convex feasibility of the approximate Bayesian stochastic optimization problem. Finally, we demonstrate the utility of our approach on an optimal staffing problem for an M/M/c queueing model.

Variational Bayesian Methods for Stochastically Constrained System Design Problems

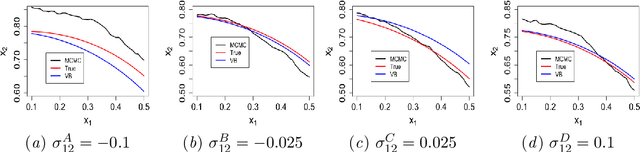
We study system design problems stated as parameterized stochastic programs with a chance-constraint set. We adopt a Bayesian approach that requires the computation of a posterior predictive integral which is usually intractable. In addition, for the problem to be a well-defined convex program, we must retain the convexity of the feasible set. Consequently, we propose a variational Bayes-based method to approximately compute the posterior predictive integral that ensures tractability and retains the convexity of the feasible set. Under certain regularity conditions, we also show that the solution set obtained using variational Bayes converges to the true solution set as the number of observations tends to infinity. We also provide bounds on the probability of qualifying a true infeasible point (with respect to the true constraints) as feasible under the VB approximation for a given number of samples.

Asymptotic Consistency of Loss-Calibrated Variational Bayes

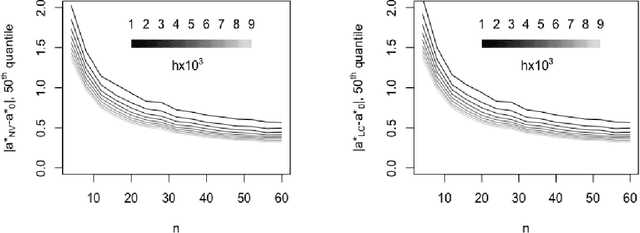
This paper establishes the asymptotic consistency of the {\it loss-calibrated variational Bayes} (LCVB) method. LCVB was proposed in~\cite{LaSiGh2011} as a method for approximately computing Bayesian posteriors in a `loss aware' manner. This methodology is also highly relevant in general data-driven decision-making contexts. Here, we not only establish the asymptotic consistency of the calibrated approximate posterior, but also the asymptotic consistency of decision rules. We also establish the asymptotic consistency of decision rules obtained from a `naive' variational Bayesian procedure.

Asymptotic Consistency of $α-$Rényi-Approximate Posteriors

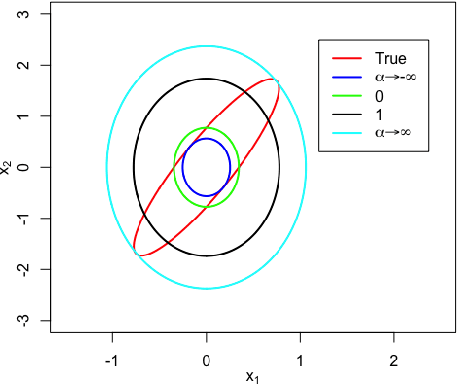
We study the asymptotic consistency properties of $\alpha$-R\'enyi approximate posteriors, a class of variational Bayesian methods that approximate an intractable Bayesian posterior with a member of a tractable family of distributions, the member chosen to minimize the $\alpha$-R\'enyi divergence from the true posterior. Unique to our work is that we consider settings with $\alpha > 1$, resulting in approximations that upperbound the log-likelihood, and consequently have wider spread than traditional variational approaches that minimize the Kullback-Liebler (KL) divergence from the posterior. Our primary result identifies sufficient conditions under which consistency holds, centering around the existence of a `good' sequence of distributions in the approximating family that possesses, among other properties, the right rate of convergence to a limit distribution. We also further characterize the good sequence by demonstrating that a sequence of distributions that converges too quickly cannot be a good sequence. We also illustrate the existence of good sequence with a number of examples. As an auxiliary result of our main theorems, we also recover the consistency of the idealized expectation propagation (EP) approximate posterior that minimizes the KL divergence from the posterior. Our results complement a growing body of work focused on the frequentist properties of variational Bayesian methods.