Asymptotic Consistency of $α-$Rényi-Approximate Posteriors

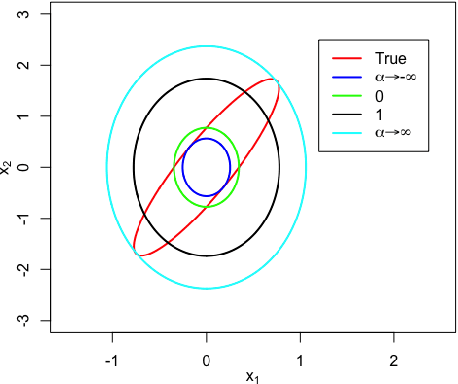
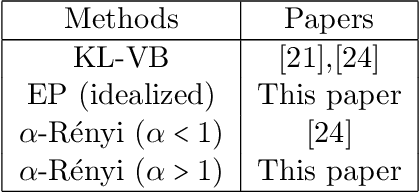
We study the asymptotic consistency properties of $\alpha$-R\'enyi approximate posteriors, a class of variational Bayesian methods that approximate an intractable Bayesian posterior with a member of a tractable family of distributions, the member chosen to minimize the $\alpha$-R\'enyi divergence from the true posterior. Unique to our work is that we consider settings with $\alpha > 1$, resulting in approximations that upperbound the log-likelihood, and consequently have wider spread than traditional variational approaches that minimize the Kullback-Liebler (KL) divergence from the posterior. Our primary result identifies sufficient conditions under which consistency holds, centering around the existence of a `good' sequence of distributions in the approximating family that possesses, among other properties, the right rate of convergence to a limit distribution. We also further characterize the good sequence by demonstrating that a sequence of distributions that converges too quickly cannot be a good sequence. We also illustrate the existence of good sequence with a number of examples. As an auxiliary result of our main theorems, we also recover the consistency of the idealized expectation propagation (EP) approximate posterior that minimizes the KL divergence from the posterior. Our results complement a growing body of work focused on the frequentist properties of variational Bayesian methods.