Offline Estimation of Controlled Markov Chains: Minimax Nonparametric Estimators and Sample Efficiency

Controlled Markov chains (CMCs) form the bedrock for model-based reinforcement learning. In this work, we consider the estimation of the transition probability matrices of a finite-state finite-control CMC using a fixed dataset, collected using a so-called logging policy, and develop minimax sample complexity bounds for nonparametric estimation of these transition probability matrices. Our results are general, and the statistical bounds depend on the logging policy through a natural mixing coefficient. We demonstrate an interesting trade-off between stronger assumptions on mixing versus requiring more samples to achieve a particular PAC-bound. We demonstrate the validity of our results under various examples, such as ergodic Markov chains, weakly ergodic inhomogeneous Markov chains, and controlled Markov chains with non-stationary Markov, episodic, and greedy controls. Lastly, we use these sample complexity bounds to establish concomitant ones for offline evaluation of stationary, Markov policies.

Distributed Sparse Regression via Penalization

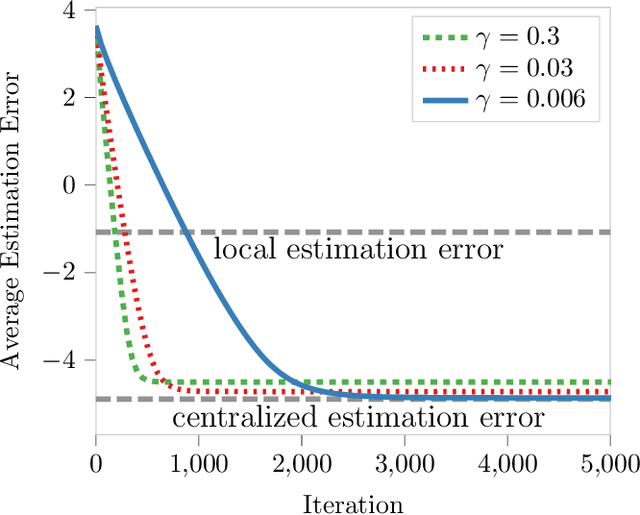
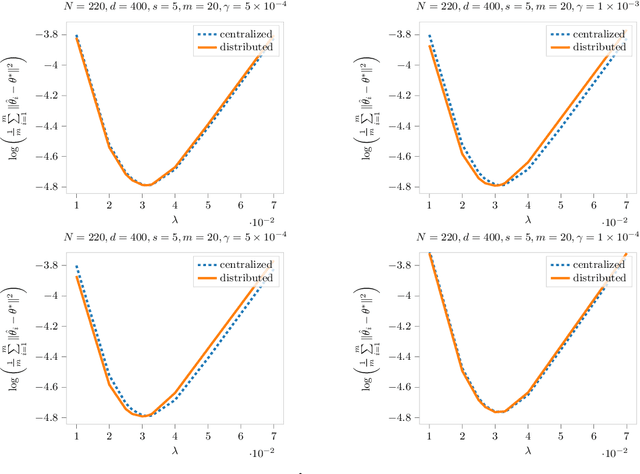
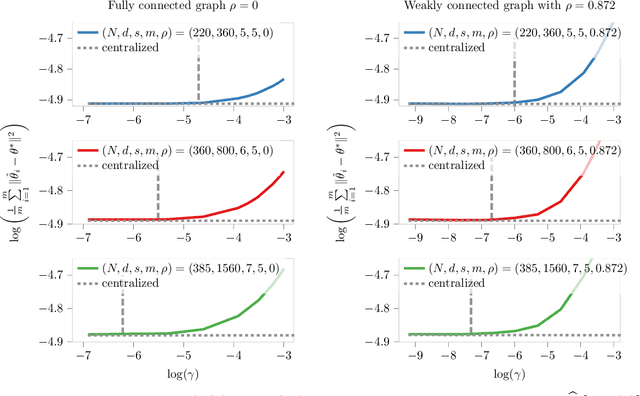
We study sparse linear regression over a network of agents, modeled as an undirected graph (with no centralized node). The estimation problem is formulated as the minimization of the sum of the local LASSO loss functions plus a quadratic penalty of the consensus constraint -- the latter being instrumental to obtain distributed solution methods. While penalty-based consensus methods have been extensively studied in the optimization literature, their statistical and computational guarantees in the high dimensional setting remain unclear. This work provides an answer to this open problem. Our contribution is two-fold. First, we establish statistical consistency of the estimator: under a suitable choice of the penalty parameter, the optimal solution of the penalized problem achieves near optimal minimax rate $\mathcal{O}(s \log d/N)$ in $\ell_2$-loss, where $s$ is the sparsity value, $d$ is the ambient dimension, and $N$ is the total sample size in the network -- this matches centralized sample rates. Second, we show that the proximal-gradient algorithm applied to the penalized problem, which naturally leads to distributed implementations, converges linearly up to a tolerance of the order of the centralized statistical error -- the rate scales as $\mathcal{O}(d)$, revealing an unavoidable speed-accuracy dilemma.Numerical results demonstrate the tightness of the derived sample rate and convergence rate scalings.

Bayesian Joint Chance Constrained Optimization: Approximations and Statistical Consistency

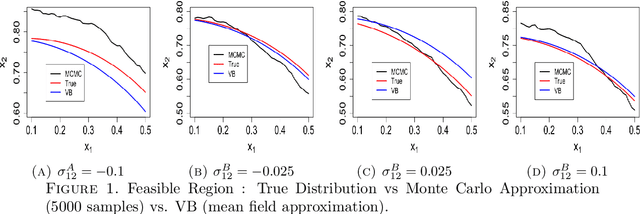
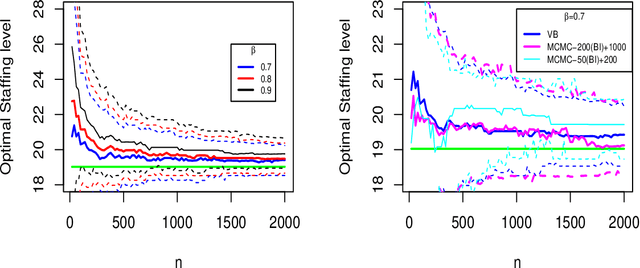
This paper considers data-driven chance-constrained stochastic optimization problems in a Bayesian framework. Bayesian posteriors afford a principled mechanism to incorporate data and prior knowledge into stochastic optimization problems. However, the computation of Bayesian posteriors is typically an intractable problem, and has spawned a large literature on approximate Bayesian computation. Here, in the context of chance-constrained optimization, we focus on the question of statistical consistency (in an appropriate sense) of the optimal value, computed using an approximate posterior distribution. To this end, we rigorously prove a frequentist consistency result demonstrating the convergence of the optimal value to the optimal value of a fixed, parameterized constrained optimization problem. We augment this by also establishing a probabilistic rate of convergence of the optimal value. We also prove the convex feasibility of the approximate Bayesian stochastic optimization problem. Finally, we demonstrate the utility of our approach on an optimal staffing problem for an M/M/c queueing model.

Estimating Stochastic Poisson Intensities Using Deep Latent Models

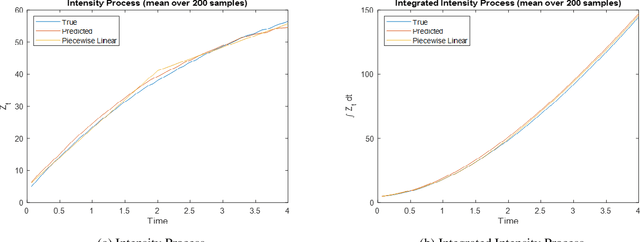
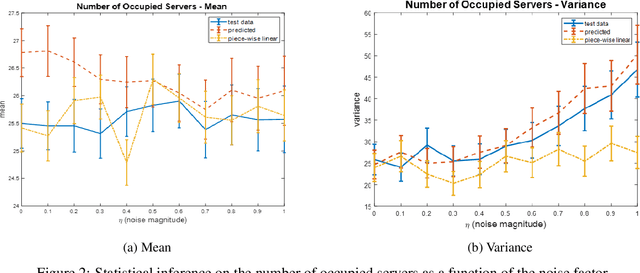
We present methodology for estimating the stochastic intensity of a doubly stochastic Poisson process. Statistical and theoretical analyses of traffic traces show that these processes are appropriate models of high intensity traffic arriving at an array of service systems. The statistical estimation of the underlying latent stochastic intensity process driving the traffic model involves a rather complicated nonlinear filtering problem. We develop a novel simulation methodology, using deep neural networks to approximate the path measures induced by the stochastic intensity process, for solving this nonlinear filtering problem. Our simulation studies demonstrate that the method is quite accurate on both in-sample estimation and on an out-of-sample performance prediction task for an infinite server queue.

Variational Bayesian Methods for Stochastically Constrained System Design Problems

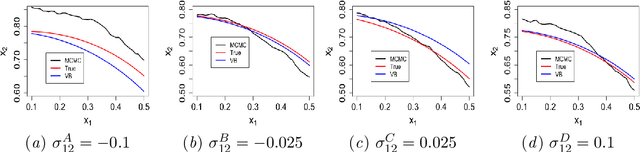
We study system design problems stated as parameterized stochastic programs with a chance-constraint set. We adopt a Bayesian approach that requires the computation of a posterior predictive integral which is usually intractable. In addition, for the problem to be a well-defined convex program, we must retain the convexity of the feasible set. Consequently, we propose a variational Bayes-based method to approximately compute the posterior predictive integral that ensures tractability and retains the convexity of the feasible set. Under certain regularity conditions, we also show that the solution set obtained using variational Bayes converges to the true solution set as the number of observations tends to infinity. We also provide bounds on the probability of qualifying a true infeasible point (with respect to the true constraints) as feasible under the VB approximation for a given number of samples.

Asymptotic Consistency of Loss-Calibrated Variational Bayes

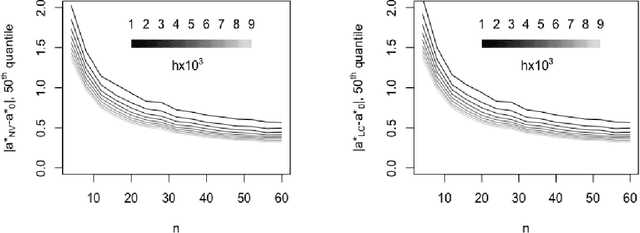
This paper establishes the asymptotic consistency of the {\it loss-calibrated variational Bayes} (LCVB) method. LCVB was proposed in~\cite{LaSiGh2011} as a method for approximately computing Bayesian posteriors in a `loss aware' manner. This methodology is also highly relevant in general data-driven decision-making contexts. Here, we not only establish the asymptotic consistency of the calibrated approximate posterior, but also the asymptotic consistency of decision rules. We also establish the asymptotic consistency of decision rules obtained from a `naive' variational Bayesian procedure.

Asymptotic Consistency of $α-$Rényi-Approximate Posteriors

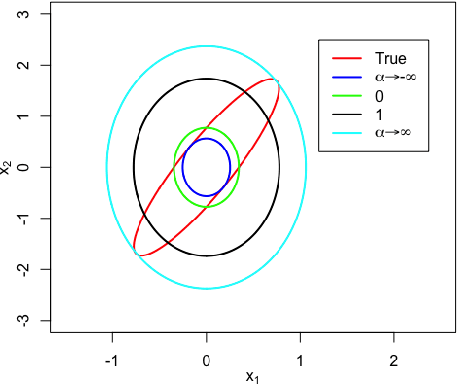
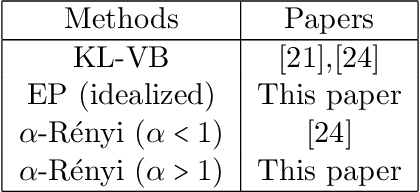
We study the asymptotic consistency properties of $\alpha$-R\'enyi approximate posteriors, a class of variational Bayesian methods that approximate an intractable Bayesian posterior with a member of a tractable family of distributions, the member chosen to minimize the $\alpha$-R\'enyi divergence from the true posterior. Unique to our work is that we consider settings with $\alpha > 1$, resulting in approximations that upperbound the log-likelihood, and consequently have wider spread than traditional variational approaches that minimize the Kullback-Liebler (KL) divergence from the posterior. Our primary result identifies sufficient conditions under which consistency holds, centering around the existence of a `good' sequence of distributions in the approximating family that possesses, among other properties, the right rate of convergence to a limit distribution. We also further characterize the good sequence by demonstrating that a sequence of distributions that converges too quickly cannot be a good sequence. We also illustrate the existence of good sequence with a number of examples. As an auxiliary result of our main theorems, we also recover the consistency of the idealized expectation propagation (EP) approximate posterior that minimizes the KL divergence from the posterior. Our results complement a growing body of work focused on the frequentist properties of variational Bayesian methods.