Offline Estimation of Controlled Markov Chains: Minimax Nonparametric Estimators and Sample Efficiency

Controlled Markov chains (CMCs) form the bedrock for model-based reinforcement learning. In this work, we consider the estimation of the transition probability matrices of a finite-state finite-control CMC using a fixed dataset, collected using a so-called logging policy, and develop minimax sample complexity bounds for nonparametric estimation of these transition probability matrices. Our results are general, and the statistical bounds depend on the logging policy through a natural mixing coefficient. We demonstrate an interesting trade-off between stronger assumptions on mixing versus requiring more samples to achieve a particular PAC-bound. We demonstrate the validity of our results under various examples, such as ergodic Markov chains, weakly ergodic inhomogeneous Markov chains, and controlled Markov chains with non-stationary Markov, episodic, and greedy controls. Lastly, we use these sample complexity bounds to establish concomitant ones for offline evaluation of stationary, Markov policies.

Set Twister for Single-hop Node Classification

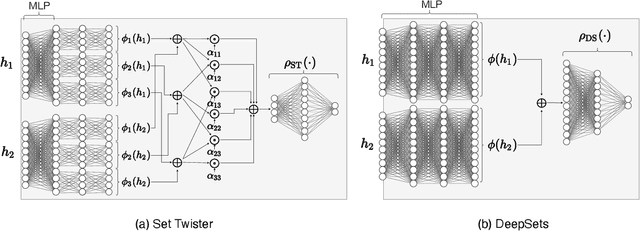
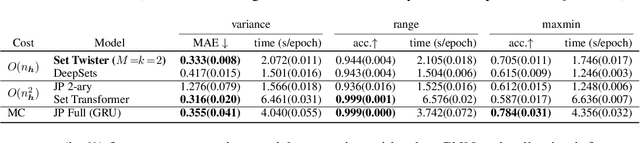
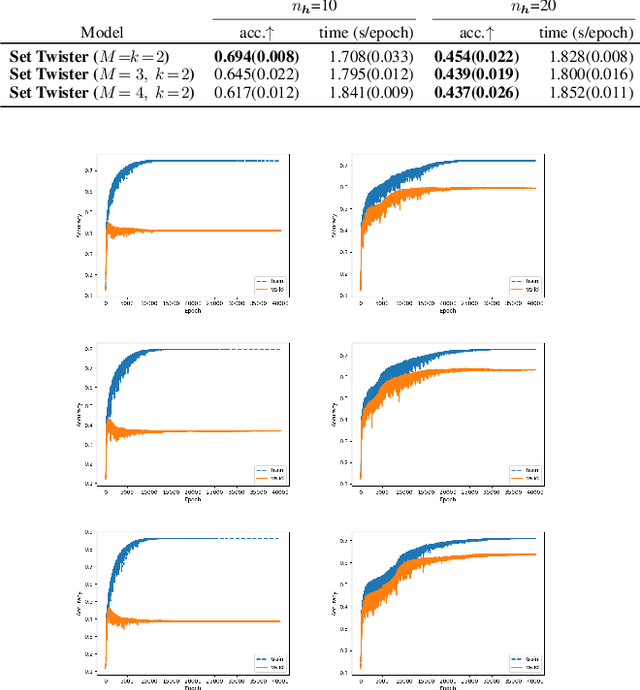
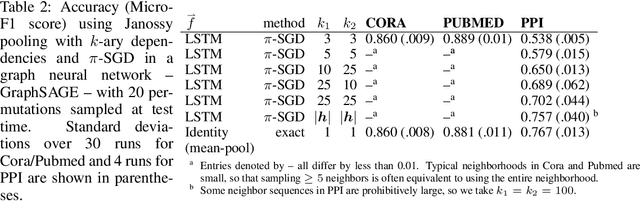
Node classification is a central task in relational learning, with the current state-of-the-art hinging on two key principles: (i) predictions are permutation-invariant to the ordering of a node's neighbors, and (ii) predictions are a function of the node's $r$-hop neighborhood topology and attributes, $r \geq 2$. Both graph neural networks and collective inference methods (e.g., belief propagation) rely on information from up to $r$-hops away. In this work, we study if the use of more powerful permutation-invariant functions can sometimes avoid the need for classifiers to collect information beyond $1$-hop. Towards this, we introduce a new architecture, the Set Twister, which generalizes DeepSets (Zaheer et al., 2017), a simple and widely-used permutation-invariant representation. Set Twister theoretically increases expressiveness of DeepSets, allowing it to capture higher-order dependencies, while keeping its simplicity and low computational cost. Empirically, we see accuracy improvements of Set Twister over DeepSets as well as a variety of graph neural networks and collective inference schemes in several tasks, while showcasing its implementation simplicity and computational efficiency.

Contextual Unsupervised Outlier Detection in Sequences

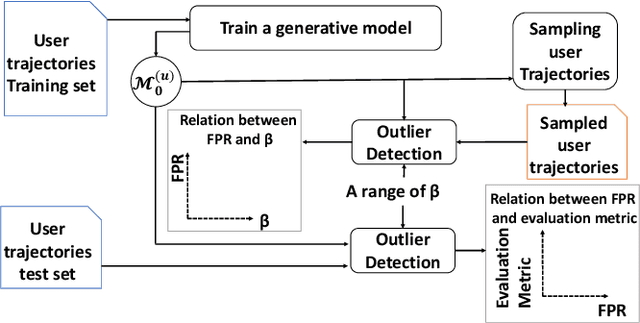
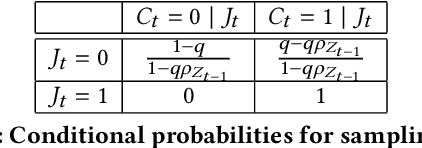
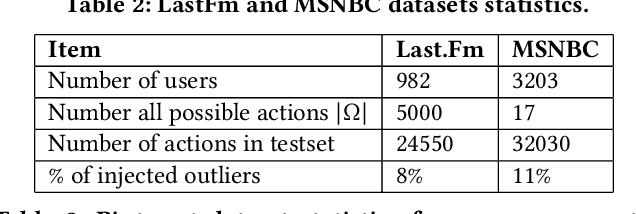
This work proposes an unsupervised learning framework for trajectory (sequence) outlier detection that combines ranking tests with user sequence models. The overall framework identifies sequence outliers at a desired false positive rate (FPR), in an otherwise parameter-free manner. We evaluate our methodology on a collection of real and simulated datasets based on user actions at the websites last.fm and msnbc.com, where we know ground truth, and demonstrate improved accuracy over existing approaches. We also apply our approach to a large real-world dataset of Pinterest and Facebook users, where we find that users tend to re-share Pinterest posts of Facebook friends significantly more than other types of users, pointing to a potential influence of Facebook friendship on sharing behavior on Pinterest.

Community detection over a heterogeneous population of non-aligned networks

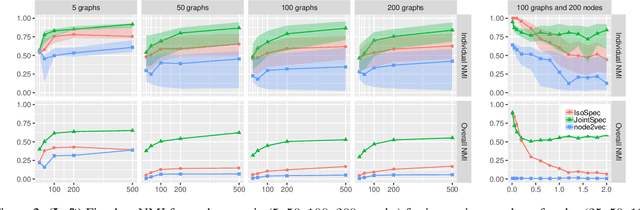
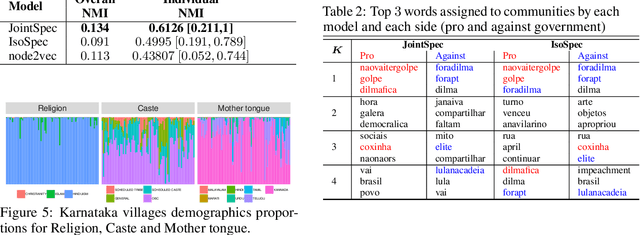
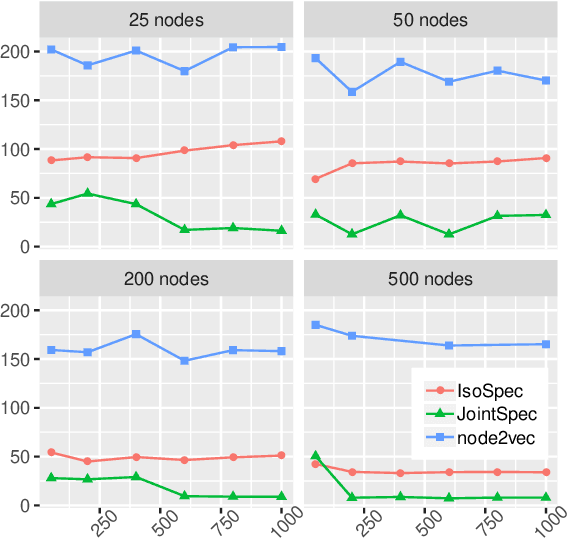
Clustering and community detection with multiple graphs have typically focused on aligned graphs, where there is a mapping between nodes across the graphs (e.g., multi-view, multi-layer, temporal graphs). However, there are numerous application areas with multiple graphs that are only partially aligned, or even unaligned. These graphs are often drawn from the same population, with communities of potentially different sizes that exhibit similar structure. In this paper, we develop a joint stochastic blockmodel (Joint SBM) to estimate shared communities across sets of heterogeneous non-aligned graphs. We derive an efficient spectral clustering approach to learn the parameters of the joint SBM. We evaluate the model on both synthetic and real-world datasets and show that the joint model is able to exploit cross-graph information to better estimate the communities compared to learning separate SBMs on each individual graph.

Relational Pooling for Graph Representations

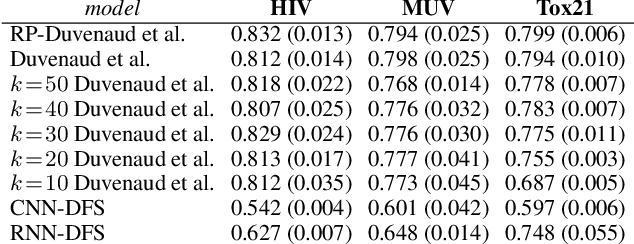
This work generalizes graph neural networks (GNNs) beyond those based on the Weisfeiler-Lehman (WL) algorithm, graph Laplacians, and graph diffusion kernels. Our approach, denoted Relational Pooling (RP), draws from the theory of finite partial exchangeability to provide a framework with maximal representation power for graphs. RP can work with existing graph representation models, and somewhat counterintuitively, can make them even more powerful than the original WL isomorphism test. Additionally, RP is the first theoretically sound framework to use architectures like Recurrent Neural Networks and Convolutional Neural Networks for graph classification. RP also has graph kernels as a special case. We demonstrate improved performance of novel RP-based graph representations over current state-of-the-art methods on a number of tasks.

Janossy Pooling: Learning Deep Permutation-Invariant Functions for Variable-Size Inputs

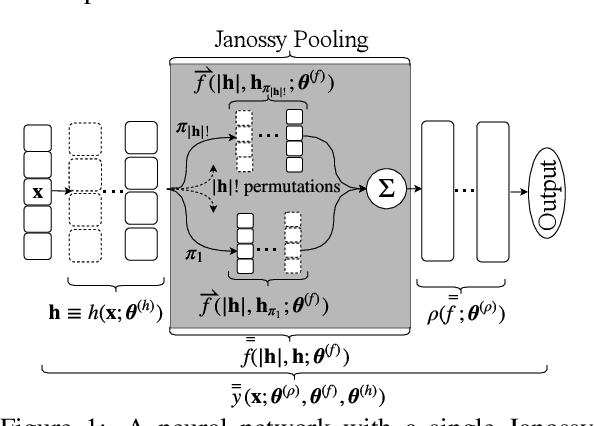
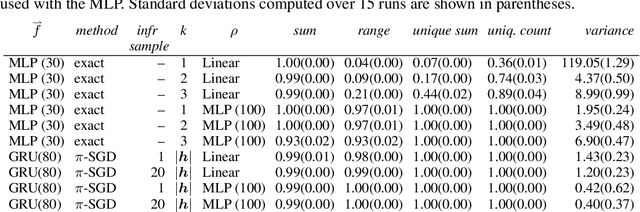
We consider a simple and overarching representation for permutation-invariant functions of sequences (or set functions). Our approach, which we call Janossy pooling, expresses a permutation-invariant function as the average of a permutation-sensitive function applied to all reorderings of the input sequence. This allows us to leverage the rich and mature literature on permutation-sensitive functions to construct novel and flexible permutation-invariant functions. If carried out naively, Janossy pooling can be computationally prohibitive. To allow computational tractability, we consider three kinds of approximations: canonical orderings of sequences, functions with k-order interactions, and stochastic optimization algorithms with random permutations. Our framework unifies a variety of existing work in the literature, and suggests possible modeling and algorithmic extensions. We explore a few in our experiments, which demonstrate improved performance over current state-of-the-art methods.

Flexible Mixture Modeling on Constrained Spaces

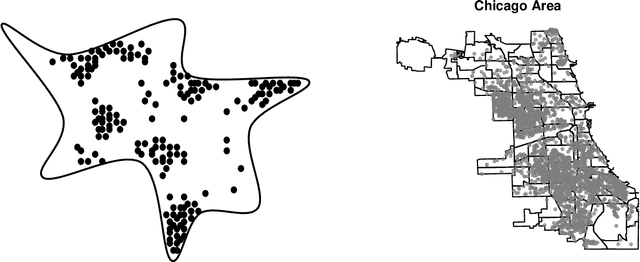
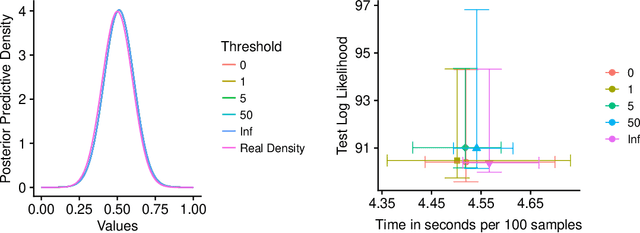
This paper addresses challenges in flexibly modeling multimodal data that lie on constrained spaces. Applications include climate or crime measurements in a geographical area, or flow-cytometry experiments, where unsuitable recordings are discarded. A simple approach to modeling such data is through the use of mixture models, with each component following an appropriate truncated distribution. Problems arise when the truncation involves complicated constraints, leading to difficulties in specifying the component distributions, and in evaluating their normalization constants. Bayesian inference over the parameters of these models results in posterior distributions that are doubly-intractable. We address this problem via an algorithm based on rejection sampling and data augmentation. We view samples from a truncated distribution as outcomes of a rejection sampling scheme, where proposals are made from a simple mixture model, and are rejected if they violate the constraints. Our scheme proceeds by imputing the rejected samples given mixture parameters, and then resampling parameters given all samples. We study two modeling approaches: mixtures of truncated components and truncated mixtures of components. In both situations, we describe exact Markov chain Monte Carlo sampling algorithms, as well as approximations that bound the number of rejected samples, achieving computational efficiency and lower variance at the cost of asymptotic bias. Overall, our methodology only requires practitioners to provide an indicator function for the set of interest. We present results on simulated data and apply our algorithm to two problems, one involving flow-cytometry data, and the other, crime recorded in the city of Chicago.

Multi-level hypothesis testing for populations of heterogeneous networks

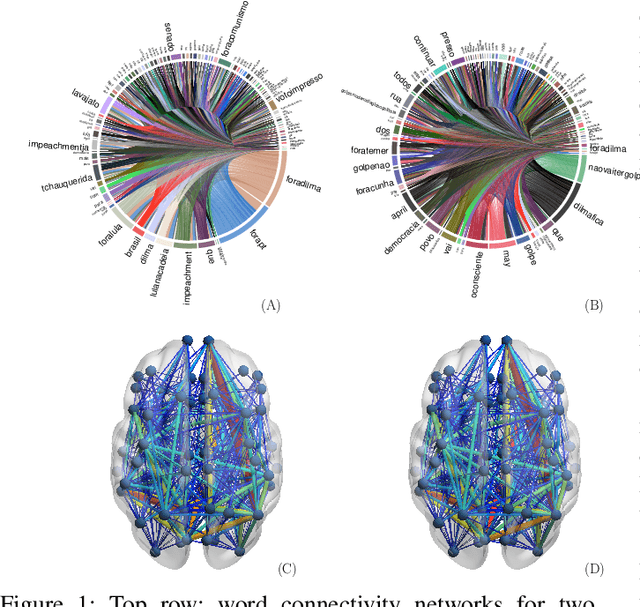
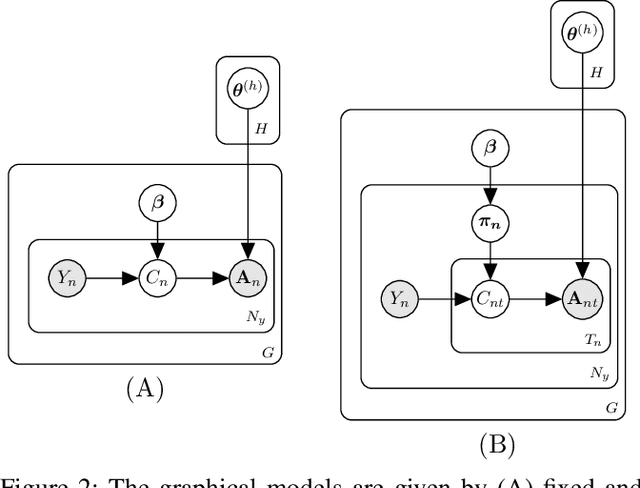
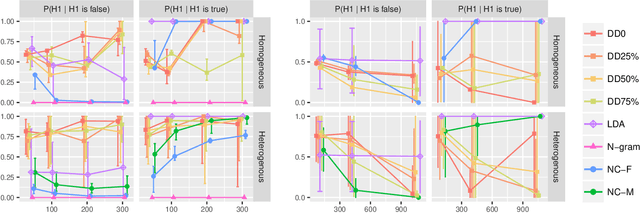
In this work, we consider hypothesis testing and anomaly detection on datasets where each observation is a weighted network. Examples of such data include brain connectivity networks from fMRI flow data, or word co-occurrence counts for populations of individuals. Current approaches to hypothesis testing for weighted networks typically requires thresholding the edge-weights, to transform the data to binary networks. This results in a loss of information, and outcomes are sensitivity to choice of threshold levels. Our work avoids this, and we consider weighted-graph observations in two situations, 1) where each graph belongs to one of two populations, and 2) where entities belong to one of two populations, with each entity possessing multiple graphs (indexed e.g. by time). Specifically, we propose a hierarchical Bayesian hypothesis testing framework that models each population with a mixture of latent space models for weighted networks, and then tests populations of networks for differences in distribution over components. Our framework is capable of population-level, entity-specific, as well as edge-specific hypothesis testing. We apply it to synthetic data and three real-world datasets: two social media datasets involving word co-occurrences from discussions on Twitter of the political unrest in Brazil, and on Instagram concerning Attention Deficit Hyperactivity Disorder (ADHD) and depression drugs, and one medical dataset involving fMRI brain-scans of human subjects. The results show that our proposed method has lower Type I error and higher statistical power compared to alternatives that need to threshold the edge weights. Moreover, they show our proposed method is better suited to deal with highly heterogeneous datasets.

Group-Representative Functional Network Estimation from Multi-Subject fMRI Data via MRF-based Image Segmentation

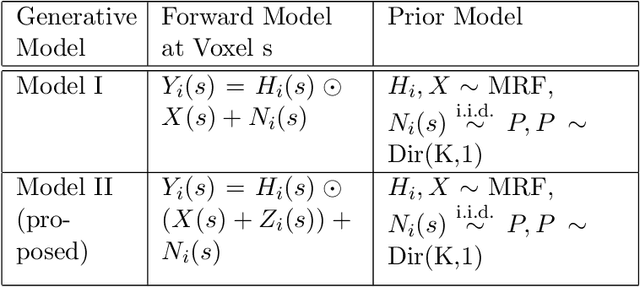
We propose a novel two-phase approach to functional network estimation of multi-subject functional Magnetic Resonance Imaging (fMRI) data, which applies model-based image segmentation to determine a group-representative connectivity map. In our approach, we first improve clustering-based Independent Component Analysis (ICA) to generate maps of components occurring consistently across subjects, and then estimate the group-representative map through MAP-MRF (Maximum a priori - Markov random field) labeling. For the latter, we provide a novel and efficient variational Bayes algorithm. We study the performance of the proposed method using synthesized data following a theoretical model, and demonstrate its viability in blind extraction of group-representative functional networks using simulated fMRI data. We anticipate the proposed method will be applied in identifying common neuronal characteristics in a population, and could be further extended to real-world clinical diagnosis.

Multiscale Shrinkage and Lévy Processes

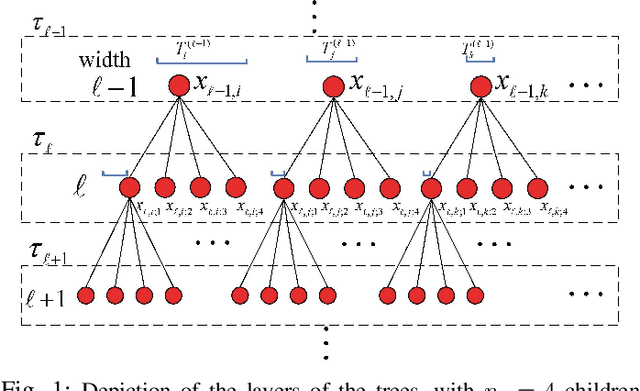
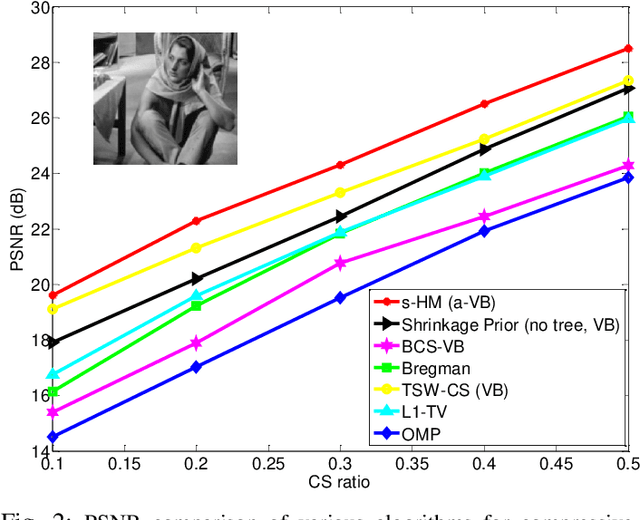
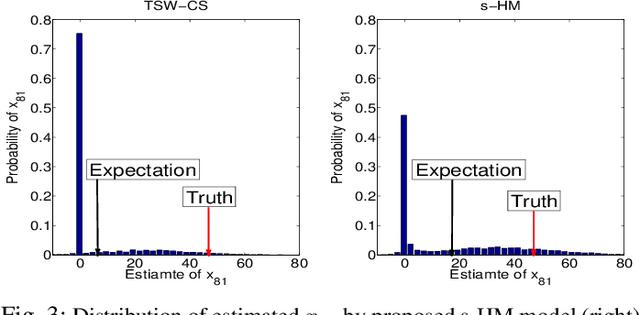
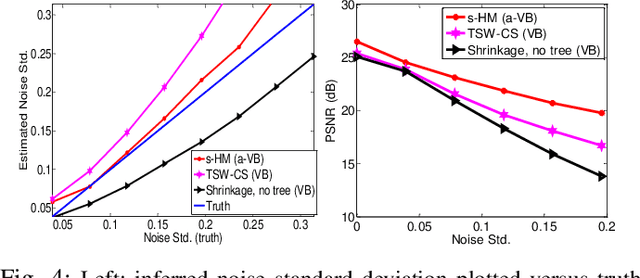
A new shrinkage-based construction is developed for a compressible vector $\boldsymbol{x}\in\mathbb{R}^n$, for cases in which the components of $\xv$ are naturally associated with a tree structure. Important examples are when $\xv$ corresponds to the coefficients of a wavelet or block-DCT representation of data. The method we consider in detail, and for which numerical results are presented, is based on increments of a gamma process. However, we demonstrate that the general framework is appropriate for many other types of shrinkage priors, all within the L\'{e}vy process family, with the gamma process a special case. Bayesian inference is carried out by approximating the posterior with samples from an MCMC algorithm, as well as by constructing a heuristic variational approximation to the posterior. We also consider expectation-maximization (EM) for a MAP (point) solution. State-of-the-art results are manifested for compressive sensing and denoising applications, the latter with spiky (non-Gaussian) noise.