Interpretable Load Forecasting via Representation Learning of Geo-distributed Meteorological Factors

Meteorological factors (MF) are crucial in day-ahead load forecasting as they significantly influence the electricity consumption behaviors of consumers. Numerous studies have incorporated MF into the load forecasting model to achieve higher accuracy. Selecting MF from one representative location or the averaged MF as the inputs of the forecasting model is a common practice. However, the difference in MF collected in various locations within a region may be significant, which poses a challenge in selecting the appropriate MF from numerous locations. A representation learning framework is proposed to extract geo-distributed MF while considering their spatial relationships. In addition, this paper employs the Shapley value in the graph-based model to reveal connections between MF collected in different locations and loads. To reduce the computational complexity of calculating the Shapley value, an acceleration method is adopted based on Monte Carlo sampling and weighted linear regression. Experiments on two real-world datasets demonstrate that the proposed method improves the day-ahead forecasting accuracy, especially in extreme scenarios such as the "accumulation temperature effect" in summer and "sudden temperature change" in winter. We also find a significant correlation between the importance of MF in different locations and the corresponding area's GDP and mainstay industry.

Uplift Modeling based on Graph Neural Network Combined with Causal Knowledge

Uplift modeling is a fundamental component of marketing effect modeling, which is commonly employed to evaluate the effects of treatments on outcomes. Through uplift modeling, we can identify the treatment with the greatest benefit. On the other side, we can identify clients who are likely to make favorable decisions in response to a certain treatment. In the past, uplift modeling approaches relied heavily on the difference-in-difference (DID) architecture, paired with a machine learning model as the estimation learner, while neglecting the link and confidential information between features. We proposed a framework based on graph neural networks that combine causal knowledge with an estimate of uplift value. Firstly, we presented a causal representation technique based on CATE (conditional average treatment effect) estimation and adjacency matrix structure learning. Secondly, we suggested a more scalable uplift modeling framework based on graph convolution networks for combining causal knowledge. Our findings demonstrate that this method works effectively for predicting uplift values, with small errors in typical simulated data, and its effectiveness has been verified in actual industry marketing data.

Double Permutation Equivariance for Knowledge Graph Completion

This work provides a formalization of Knowledge Graphs (KGs) as a new class of graphs that we denote doubly exchangeable attributed graphs, where node and pairwise (joint 2-node) representations must be equivariant to permutations of both node ids and edge (& node) attributes (relations & node features). Double-permutation equivariant KG representations open a new research direction in KGs. We show that this equivariance imposes a structural representation of relations that allows neural networks to perform complex logical reasoning tasks in KGs. Finally, we introduce a general blueprint for such equivariant representations and test a simple GNN-based double-permutation equivariant neural architecture that achieve 100% Hits@10 test accuracy in both the WN18RRv1 and NELL995v1 inductive KG completion tasks, and can accurately perform logical reasoning tasks that no existing methods can perform, to the best of our knowledge.

Bias Challenges in Counterfactual Data Augmentation

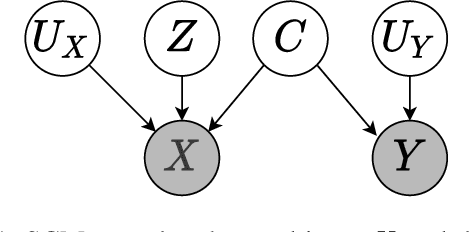
Deep learning models tend not to be out-of-distribution robust primarily due to their reliance on spurious features to solve the task. Counterfactual data augmentations provide a general way of (approximately) achieving representations that are counterfactual-invariant to spurious features, a requirement for out-of-distribution (OOD) robustness. In this work, we show that counterfactual data augmentations may not achieve the desired counterfactual-invariance if the augmentation is performed by a context-guessing machine, an abstract machine that guesses the most-likely context of a given input. We theoretically analyze the invariance imposed by such counterfactual data augmentations and describe an exemplar NLP task where counterfactual data augmentation by a context-guessing machine does not lead to robust OOD classifiers.

OOD Link Prediction Generalization Capabilities of Message-Passing GNNs in Larger Test Graphs

This work provides the first theoretical study on the ability of graph Message Passing Neural Networks (gMPNNs) -- such as Graph Neural Networks (GNNs) -- to perform inductive out-of-distribution (OOD) link prediction tasks, where deployment (test) graph sizes are larger than training graphs. We first prove non-asymptotic bounds showing that link predictors based on permutation-equivariant (structural) node embeddings obtained by gMPNNs can converge to a random guess as test graphs get larger. We then propose a theoretically-sound gMPNN that outputs structural pairwise (2-node) embeddings and prove non-asymptotic bounds showing that, as test graphs grow, these embeddings converge to embeddings of a continuous function that retains its ability to predict links OOD. Empirical results on random graphs show agreement with our theoretical results.

Set Twister for Single-hop Node Classification

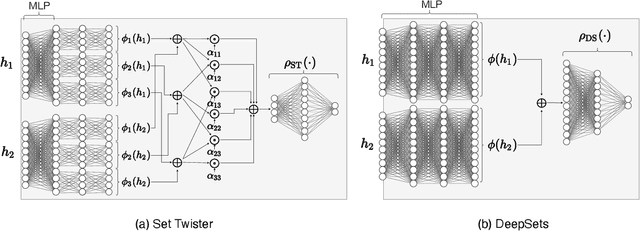
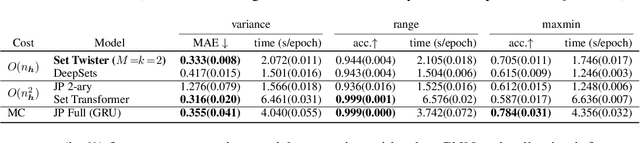
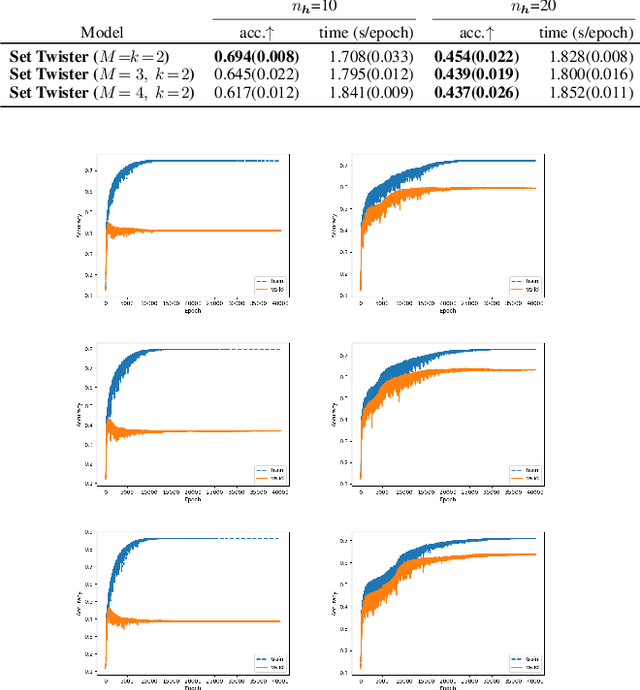
Node classification is a central task in relational learning, with the current state-of-the-art hinging on two key principles: (i) predictions are permutation-invariant to the ordering of a node's neighbors, and (ii) predictions are a function of the node's $r$-hop neighborhood topology and attributes, $r \geq 2$. Both graph neural networks and collective inference methods (e.g., belief propagation) rely on information from up to $r$-hops away. In this work, we study if the use of more powerful permutation-invariant functions can sometimes avoid the need for classifiers to collect information beyond $1$-hop. Towards this, we introduce a new architecture, the Set Twister, which generalizes DeepSets (Zaheer et al., 2017), a simple and widely-used permutation-invariant representation. Set Twister theoretically increases expressiveness of DeepSets, allowing it to capture higher-order dependencies, while keeping its simplicity and low computational cost. Empirically, we see accuracy improvements of Set Twister over DeepSets as well as a variety of graph neural networks and collective inference schemes in several tasks, while showcasing its implementation simplicity and computational efficiency.

Size-Invariant Graph Representations for Graph Classification Extrapolations

In general, graph representation learning methods assume that the test and train data come from the same distribution. In this work we consider an underexplored area of an otherwise rapidly developing field of graph representation learning: The task of out-of-distribution (OOD) graph classification, where train and test data have different distributions, with test data unavailable during training. Our work shows it is possible to use a causal model to learn approximately invariant representations that better extrapolate between train and test data. Finally, we conclude with synthetic and real-world dataset experiments showcasing the benefits of representations that are invariant to train/test distribution shifts.