Set Twister for Single-hop Node Classification
Paper and Code
Dec 17, 2021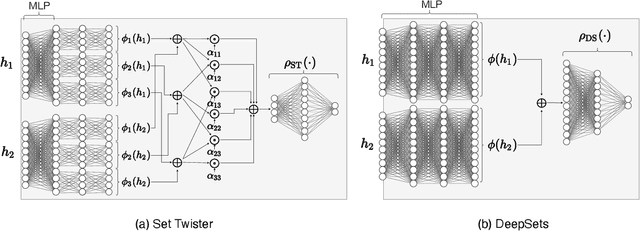

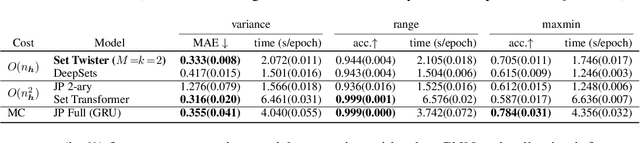
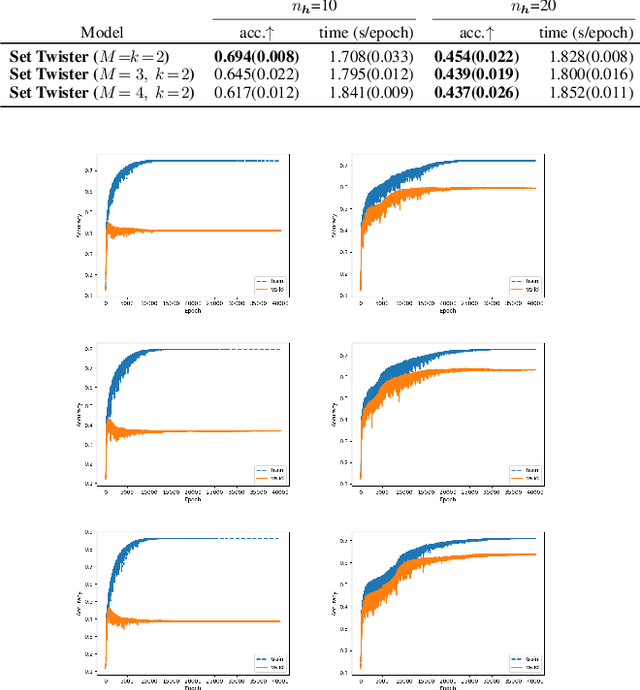
Node classification is a central task in relational learning, with the current state-of-the-art hinging on two key principles: (i) predictions are permutation-invariant to the ordering of a node's neighbors, and (ii) predictions are a function of the node's $r$-hop neighborhood topology and attributes, $r \geq 2$. Both graph neural networks and collective inference methods (e.g., belief propagation) rely on information from up to $r$-hops away. In this work, we study if the use of more powerful permutation-invariant functions can sometimes avoid the need for classifiers to collect information beyond $1$-hop. Towards this, we introduce a new architecture, the Set Twister, which generalizes DeepSets (Zaheer et al., 2017), a simple and widely-used permutation-invariant representation. Set Twister theoretically increases expressiveness of DeepSets, allowing it to capture higher-order dependencies, while keeping its simplicity and low computational cost. Empirically, we see accuracy improvements of Set Twister over DeepSets as well as a variety of graph neural networks and collective inference schemes in several tasks, while showcasing its implementation simplicity and computational efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge