Semi-off-Policy Reinforcement Learning for Vision-Language Slow-thinking Reasoning

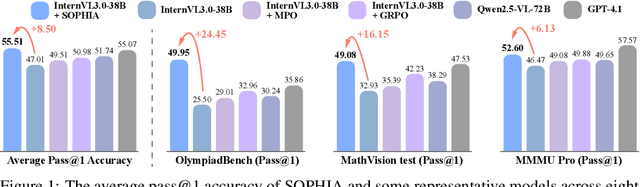
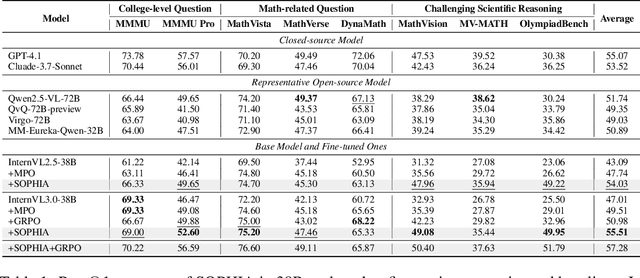
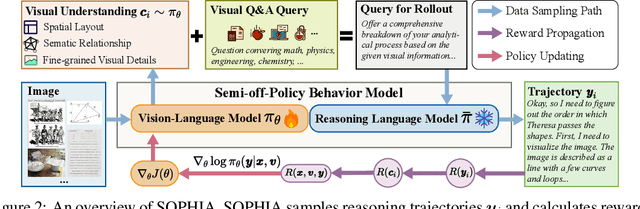
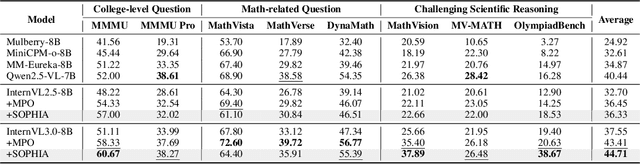
Enhancing large vision-language models (LVLMs) with visual slow-thinking reasoning is crucial for solving complex multimodal tasks. However, since LVLMs are mainly trained with vision-language alignment, it is difficult to adopt on-policy reinforcement learning (RL) to develop the slow thinking ability because the rollout space is restricted by its initial abilities. Off-policy RL offers a way to go beyond the current policy, but directly distilling trajectories from external models may cause visual hallucinations due to mismatched visual perception abilities across models. To address these issues, this paper proposes SOPHIA, a simple and scalable Semi-Off-Policy RL for vision-language slow-tHInking reAsoning. SOPHIA builds a semi-off-policy behavior model by combining on-policy visual understanding from a trainable LVLM with off-policy slow-thinking reasoning from a language model, assigns outcome-based rewards to reasoning, and propagates visual rewards backward. Then LVLM learns slow-thinking reasoning ability from the obtained reasoning trajectories using propagated rewards via off-policy RL algorithms. Extensive experiments with InternVL2.5 and InternVL3.0 with 8B and 38B sizes show the effectiveness of SOPHIA. Notably, SOPHIA improves InternVL3.0-38B by 8.50% in average, reaching state-of-the-art performance among open-source LVLMs on multiple multimodal reasoning benchmarks, and even outperforms some closed-source models (e.g., GPT-4.1) on the challenging MathVision and OlympiadBench, achieving 49.08% and 49.95% pass@1 accuracy, respectively. Analysis shows SOPHIA outperforms supervised fine-tuning and direct on-policy RL methods, offering a better policy initialization for further on-policy training.

RIG: Synergizing Reasoning and Imagination in End-to-End Generalist Policy

Reasoning before action and imagining potential outcomes (i.e., world models) are essential for embodied agents operating in complex open-world environments. Yet, prior work either incorporates only one of these abilities in an end-to-end agent or integrates multiple specialized models into an agent system, limiting the learning efficiency and generalization of the policy. Thus, this paper makes the first attempt to synergize Reasoning and Imagination in an end-to-end Generalist policy, termed RIG. To train RIG in an end-to-end manner, we construct a data pipeline that progressively integrates and enriches the content of imagination and reasoning in the trajectories collected from existing agents. The joint learning of reasoning and next image generation explicitly models the inherent correlation between reasoning, action, and dynamics of environments, and thus exhibits more than $17\times$ sample efficiency improvements and generalization in comparison with previous works. During inference, RIG first reasons about the next action, produces potential action, and then predicts the action outcomes, which offers the agent a chance to review and self-correct based on the imagination before taking real actions. Experimental results show that the synergy of reasoning and imagination not only improves the robustness, generalization, and interoperability of generalist policy but also enables test-time scaling to enhance overall performance.

Exploring the Limit of Outcome Reward for Learning Mathematical Reasoning

Reasoning abilities, especially those for solving complex math problems, are crucial components of general intelligence. Recent advances by proprietary companies, such as o-series models of OpenAI, have made remarkable progress on reasoning tasks. However, the complete technical details remain unrevealed, and the techniques that are believed certainly to be adopted are only reinforcement learning (RL) and the long chain of thoughts. This paper proposes a new RL framework, termed OREAL, to pursue the performance limit that can be achieved through \textbf{O}utcome \textbf{RE}w\textbf{A}rd-based reinforcement \textbf{L}earning for mathematical reasoning tasks, where only binary outcome rewards are easily accessible. We theoretically prove that behavior cloning on positive trajectories from best-of-N (BoN) sampling is sufficient to learn the KL-regularized optimal policy in binary feedback environments. This formulation further implies that the rewards of negative samples should be reshaped to ensure the gradient consistency between positive and negative samples. To alleviate the long-existing difficulties brought by sparse rewards in RL, which are even exacerbated by the partial correctness of the long chain of thought for reasoning tasks, we further apply a token-level reward model to sample important tokens in reasoning trajectories for learning. With OREAL, for the first time, a 7B model can obtain 94.0 pass@1 accuracy on MATH-500 through RL, being on par with 32B models. OREAL-32B also surpasses previous 32B models trained by distillation with 95.0 pass@1 accuracy on MATH-500. Our investigation also indicates the importance of initial policy models and training queries for RL. Code, models, and data will be released to benefit future research\footnote{https://github.com/InternLM/OREAL}.

InternVideo2.5: Empowering Video MLLMs with Long and Rich Context Modeling

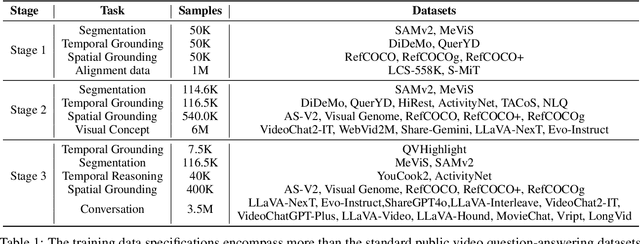
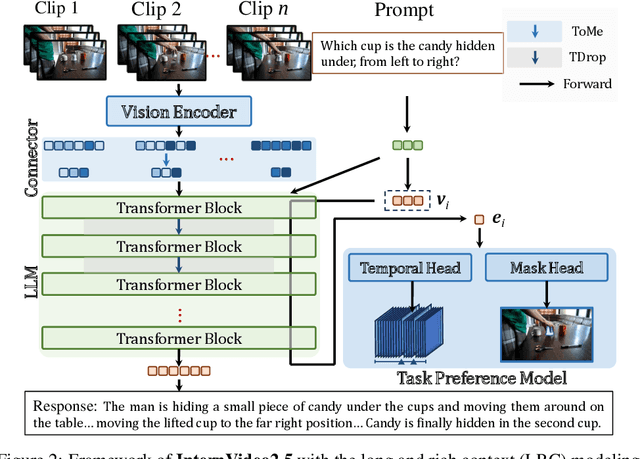
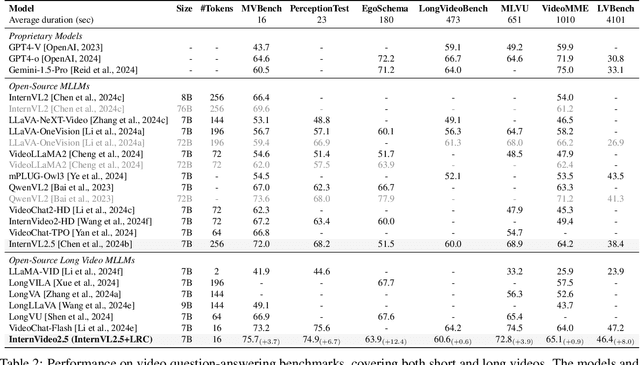
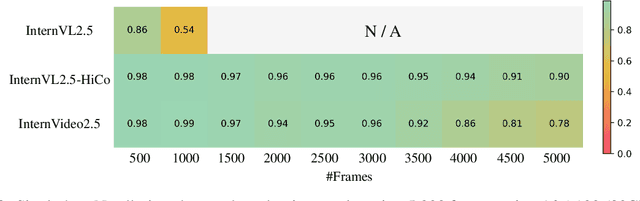
This paper aims to improve the performance of video multimodal large language models (MLLM) via long and rich context (LRC) modeling. As a result, we develop a new version of InternVideo2.5 with a focus on enhancing the original MLLMs' ability to perceive fine-grained details and capture long-form temporal structure in videos. Specifically, our approach incorporates dense vision task annotations into MLLMs using direct preference optimization and develops compact spatiotemporal representations through adaptive hierarchical token compression. Experimental results demonstrate this unique design of LRC greatly improves the results of video MLLM in mainstream video understanding benchmarks (short & long), enabling the MLLM to memorize significantly longer video inputs (at least 6x longer than the original), and master specialized vision capabilities like object tracking and segmentation. Our work highlights the importance of multimodal context richness (length and fineness) in empowering MLLM's innate abilites (focus and memory), providing new insights for future research on video MLLM. Code and models are available at https://github.com/OpenGVLab/InternVideo/tree/main/InternVideo2.5

VideoChat-Flash: Hierarchical Compression for Long-Context Video Modeling

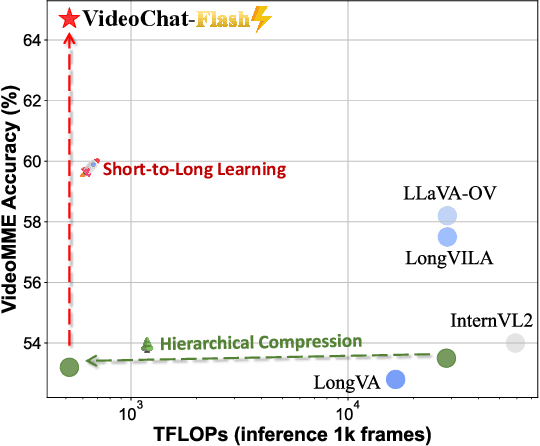
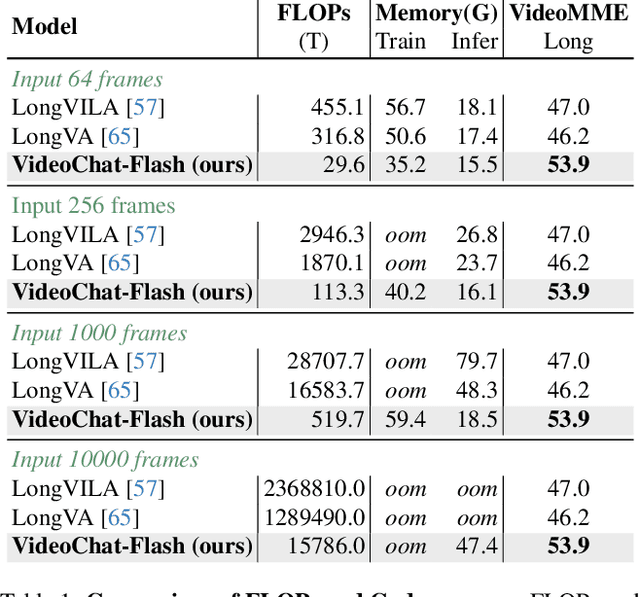
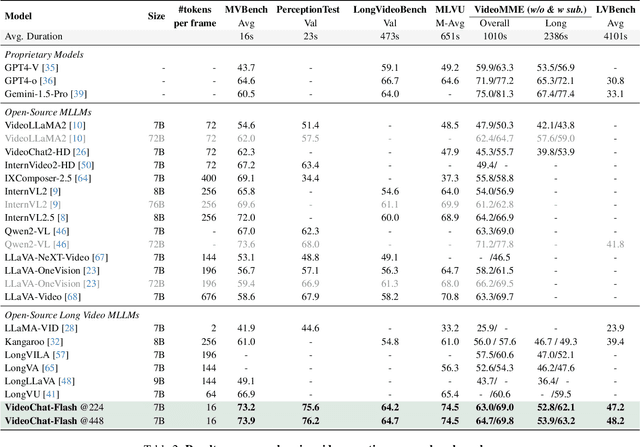
Long-context modeling is a critical capability for multimodal large language models (MLLMs), enabling them to process long-form contents with implicit memorization. Despite its advances, handling extremely long videos remains challenging due to the difficulty in maintaining crucial features over extended sequences. This paper introduces a Hierarchical visual token Compression (HiCo) method designed for high-fidelity representation and a practical context modeling system VideoChat-Flash tailored for multimodal long-sequence processing. HiCo capitalizes on the redundancy of visual information in long videos to compress long video context from the clip-level to the video-level, reducing the compute significantly while preserving essential details. VideoChat-Flash features a multi-stage short-to-long learning scheme, a rich dataset of real-world long videos named LongVid, and an upgraded "Needle-In-A-video-Haystack" (NIAH) for evaluating context capacities. In extensive experiments, VideoChat-Flash shows the leading performance on both mainstream long and short video benchmarks at the 7B model scale. It firstly gets 99.1% accuracy over 10,000 frames in NIAH among open-source models.

Differentiable Model Scaling using Differentiable Topk

Over the past few years, as large language models have ushered in an era of intelligence emergence, there has been an intensified focus on scaling networks. Currently, many network architectures are designed manually, often resulting in sub-optimal configurations. Although Neural Architecture Search (NAS) methods have been proposed to automate this process, they suffer from low search efficiency. This study introduces Differentiable Model Scaling (DMS), increasing the efficiency for searching optimal width and depth in networks. DMS can model both width and depth in a direct and fully differentiable way, making it easy to optimize. We have evaluated our DMS across diverse tasks, ranging from vision tasks to NLP tasks and various network architectures, including CNNs and Transformers. Results consistently indicate that our DMS can find improved structures and outperforms state-of-the-art NAS methods. Specifically, for image classification on ImageNet, our DMS improves the top-1 accuracy of EfficientNet-B0 and Deit-Tiny by 1.4% and 0.6%, respectively, and outperforms the state-of-the-art zero-shot NAS method, ZiCo, by 1.3% while requiring only 0.4 GPU days for searching. For object detection on COCO, DMS improves the mAP of Yolo-v8-n by 2.0%. For language modeling, our pruned Llama-7B outperforms the prior method with lower perplexity and higher zero-shot classification accuracy. We will release our code in the future.

Double Permutation Equivariance for Knowledge Graph Completion

This work provides a formalization of Knowledge Graphs (KGs) as a new class of graphs that we denote doubly exchangeable attributed graphs, where node and pairwise (joint 2-node) representations must be equivariant to permutations of both node ids and edge (& node) attributes (relations & node features). Double-permutation equivariant KG representations open a new research direction in KGs. We show that this equivariance imposes a structural representation of relations that allows neural networks to perform complex logical reasoning tasks in KGs. Finally, we introduce a general blueprint for such equivariant representations and test a simple GNN-based double-permutation equivariant neural architecture that achieve 100% Hits@10 test accuracy in both the WN18RRv1 and NELL995v1 inductive KG completion tasks, and can accurately perform logical reasoning tasks that no existing methods can perform, to the best of our knowledge.

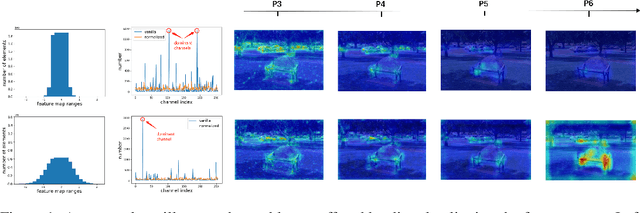
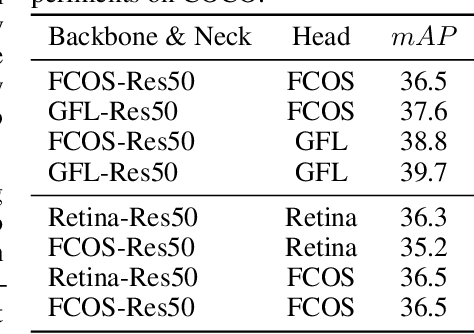
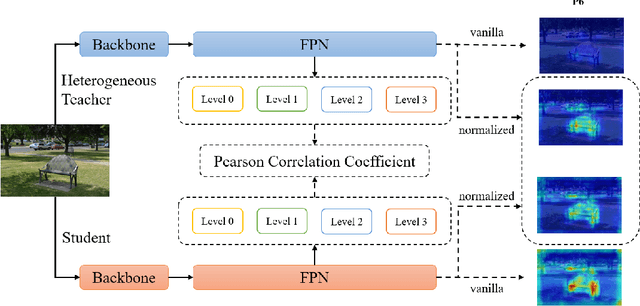
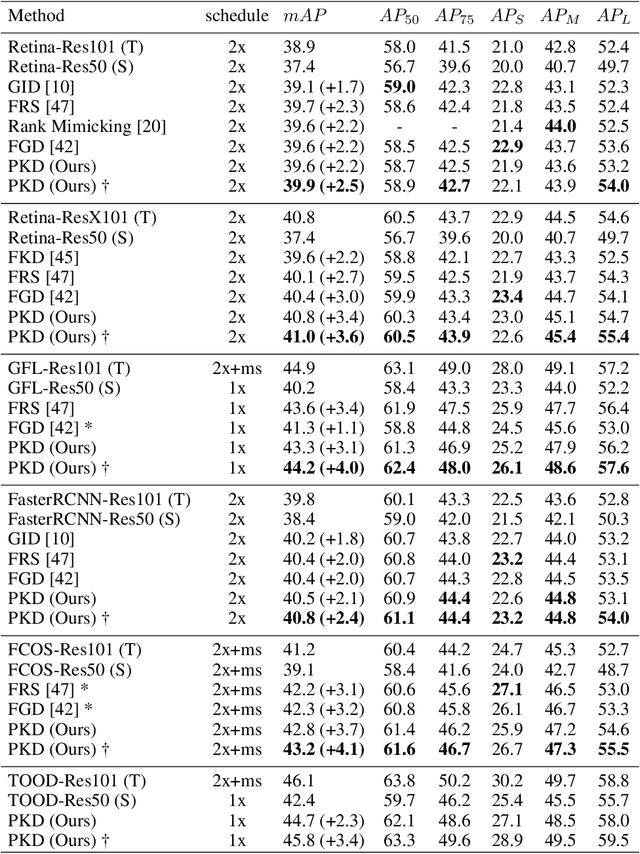
PKD: General Distillation Framework for Object Detectors via Pearson Correlation Coefficient

Knowledge distillation(KD) is a widely-used technique to train compact models in object detection. However, there is still a lack of study on how to distill between heterogeneous detectors. In this paper, we empirically find that better FPN features from a heterogeneous teacher detector can help the student although their detection heads and label assignments are different. However, directly aligning the feature maps to distill detectors suffers from two problems. First, the difference in feature magnitude between the teacher and the student could enforce overly strict constraints on the student. Second, the FPN stages and channels with large feature magnitude from the teacher model could dominate the gradient of distillation loss, which will overwhelm the effects of other features in KD and introduce much noise. To address the above issues, we propose to imitate features with Pearson Correlation Coefficient to focus on the relational information from the teacher and relax constraints on the magnitude of the features. Our method consistently outperforms the existing detection KD methods and works for both homogeneous and heterogeneous student-teacher pairs. Furthermore, it converges faster. With a powerful MaskRCNN-Swin detector as the teacher, ResNet-50 based RetinaNet and FCOS achieve 41.5% and 43.9% mAP on COCO2017, which are 4.1\% and 4.8\% higher than the baseline, respectively.

On the Equivalence Between Temporal and Static Graph Representations for Observational Predictions

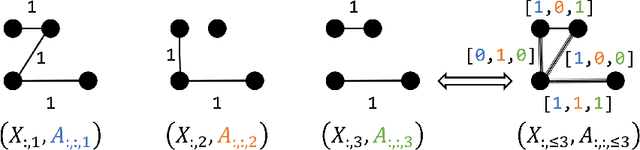
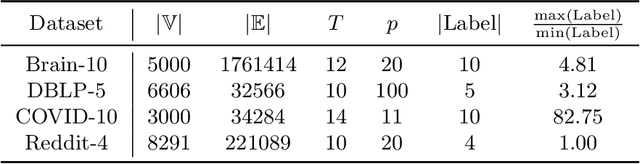
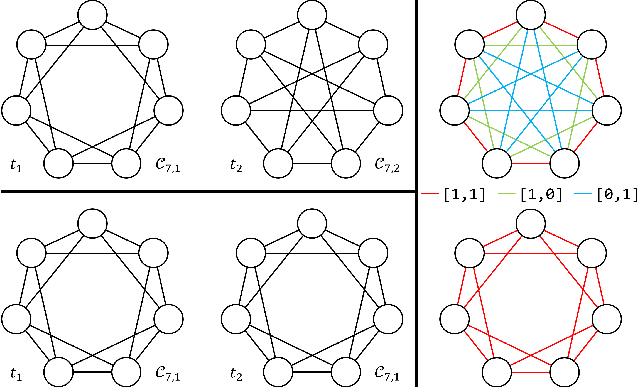
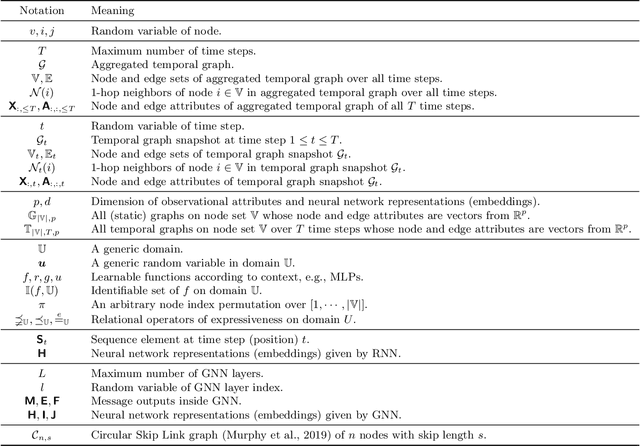
In this work we formalize the (pure observational) task of predicting node attribute evolution in temporal graphs. We show that node representations of temporal graphs can be cast into two distinct frameworks: (a) The de-facto standard approach, which we denote {\em time-and-graph}, where equivariant graph (e.g., GNN) and sequence (e.g., RNN) representations are intertwined to represent the temporal evolution of the graph; and (b) an approach that we denote {\em time-then-graph}, where the sequences describing the node and edge dynamics are represented first (e.g., RNN), then fed as node and edge attributes into a (static) equivariant graph representation that comes after (e.g., GNN). In real-world datasets, we show that our {\em time-then-graph} framework achieves the same prediction performance as state-of-the-art {\em time-and-graph} methods. Interestingly, {\em time-then-graph} representations have an expressiveness advantage over {\em time-and-graph} representations when both use component GNNs that are not most-expressive (e.g., 1-Weisfeiler-Lehman GNNs). We introduce a task where this expressiveness advantage allows {\em time-then-graph} methods to succeed while state-of-the-art {\em time-and-graph} methods fail.

Channel-wise Distillation for Semantic Segmentation

Knowledge distillation (KD) has been proven to be a simple and effective tool for training compact models. Almost all KD variants for semantic segmentation align the student and teacher networks' feature maps in the spatial domain, typically by minimizing point-wise and/or pair-wise discrepancy. Observing that in semantic segmentation, some layers' feature activations of each channel tend to encode saliency of scene categories (analogue to class activation mapping), we propose to align features channel-wise between the student and teacher networks. To this end, we first transform the feature map of each channel into a distribution using softmax normalization, and then minimize the Kullback-Leibler (KL) divergence of the corresponding channels of the two networks. By doing so, our method focuses on mimicking the soft distributions of channels between networks. In particular, the KL divergence enables learning to pay more attention to the most salient regions of the channel-wise maps, presumably corresponding to the most useful signals for semantic segmentation. Experiments demonstrate that our channel-wise distillation outperforms almost all existing spatial distillation methods for semantic segmentation considerably, and requires less computational cost during training. We consistently achieve superior performance on three benchmarks with various network structures. Code is available at: https://git.io/ChannelDis