On the Equivalence Between Temporal and Static Graph Representations for Observational Predictions
Paper and Code
Mar 12, 2021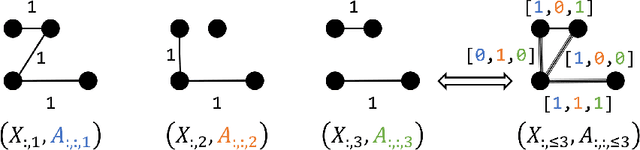
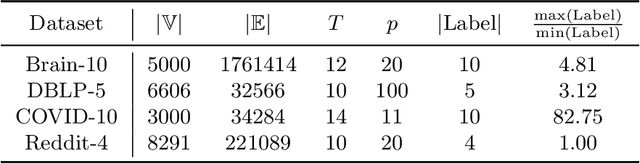
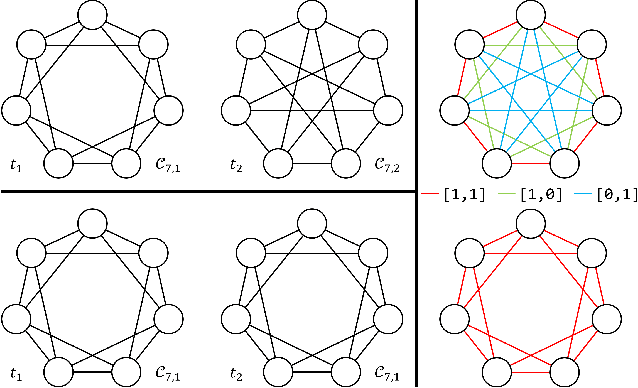
In this work we formalize the (pure observational) task of predicting node attribute evolution in temporal graphs. We show that node representations of temporal graphs can be cast into two distinct frameworks: (a) The de-facto standard approach, which we denote {\em time-and-graph}, where equivariant graph (e.g., GNN) and sequence (e.g., RNN) representations are intertwined to represent the temporal evolution of the graph; and (b) an approach that we denote {\em time-then-graph}, where the sequences describing the node and edge dynamics are represented first (e.g., RNN), then fed as node and edge attributes into a (static) equivariant graph representation that comes after (e.g., GNN). In real-world datasets, we show that our {\em time-then-graph} framework achieves the same prediction performance as state-of-the-art {\em time-and-graph} methods. Interestingly, {\em time-then-graph} representations have an expressiveness advantage over {\em time-and-graph} representations when both use component GNNs that are not most-expressive (e.g., 1-Weisfeiler-Lehman GNNs). We introduce a task where this expressiveness advantage allows {\em time-then-graph} methods to succeed while state-of-the-art {\em time-and-graph} methods fail.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge