Janossy Pooling: Learning Deep Permutation-Invariant Functions for Variable-Size Inputs
Paper and Code
Nov 26, 2018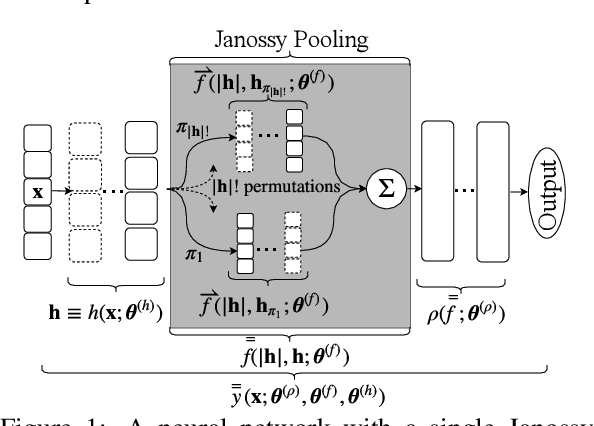
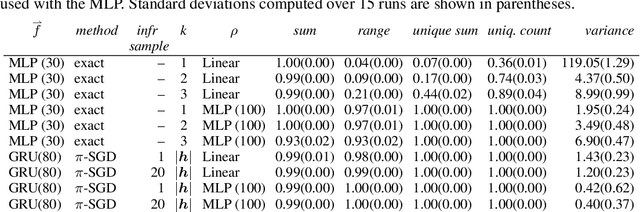
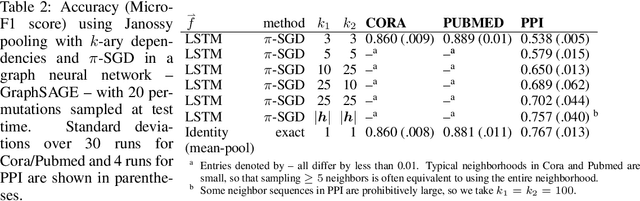
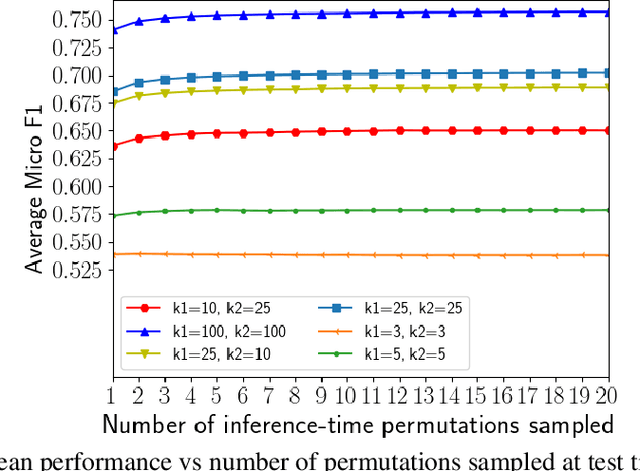
We consider a simple and overarching representation for permutation-invariant functions of sequences (or set functions). Our approach, which we call Janossy pooling, expresses a permutation-invariant function as the average of a permutation-sensitive function applied to all reorderings of the input sequence. This allows us to leverage the rich and mature literature on permutation-sensitive functions to construct novel and flexible permutation-invariant functions. If carried out naively, Janossy pooling can be computationally prohibitive. To allow computational tractability, we consider three kinds of approximations: canonical orderings of sequences, functions with k-order interactions, and stochastic optimization algorithms with random permutations. Our framework unifies a variety of existing work in the literature, and suggests possible modeling and algorithmic extensions. We explore a few in our experiments, which demonstrate improved performance over current state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge