Multi-level hypothesis testing for populations of heterogeneous networks
Paper and Code
Sep 07, 2018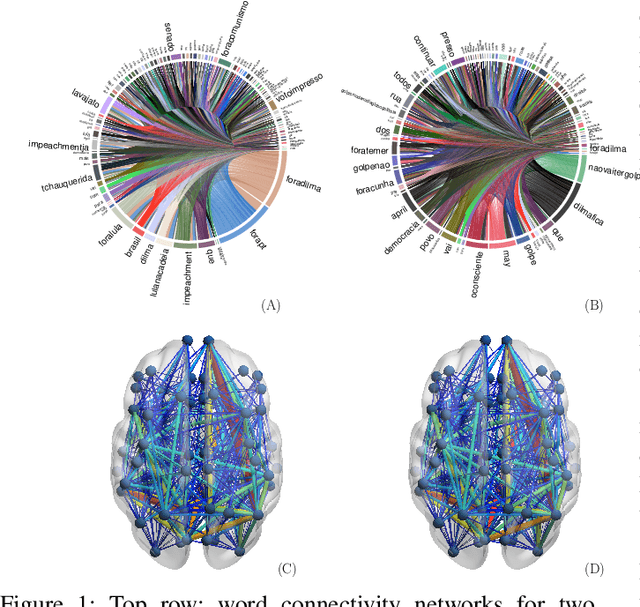
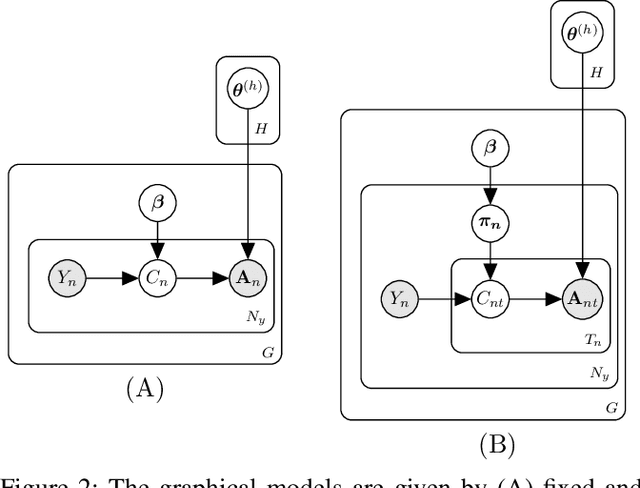
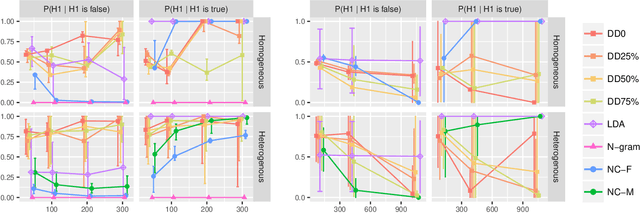
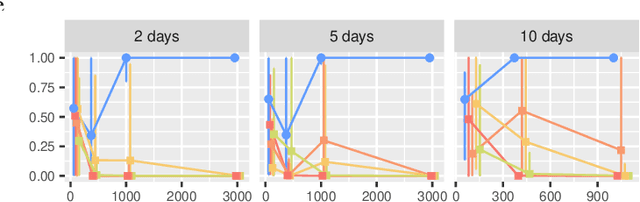
In this work, we consider hypothesis testing and anomaly detection on datasets where each observation is a weighted network. Examples of such data include brain connectivity networks from fMRI flow data, or word co-occurrence counts for populations of individuals. Current approaches to hypothesis testing for weighted networks typically requires thresholding the edge-weights, to transform the data to binary networks. This results in a loss of information, and outcomes are sensitivity to choice of threshold levels. Our work avoids this, and we consider weighted-graph observations in two situations, 1) where each graph belongs to one of two populations, and 2) where entities belong to one of two populations, with each entity possessing multiple graphs (indexed e.g. by time). Specifically, we propose a hierarchical Bayesian hypothesis testing framework that models each population with a mixture of latent space models for weighted networks, and then tests populations of networks for differences in distribution over components. Our framework is capable of population-level, entity-specific, as well as edge-specific hypothesis testing. We apply it to synthetic data and three real-world datasets: two social media datasets involving word co-occurrences from discussions on Twitter of the political unrest in Brazil, and on Instagram concerning Attention Deficit Hyperactivity Disorder (ADHD) and depression drugs, and one medical dataset involving fMRI brain-scans of human subjects. The results show that our proposed method has lower Type I error and higher statistical power compared to alternatives that need to threshold the edge weights. Moreover, they show our proposed method is better suited to deal with highly heterogeneous datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge