Multiscale Shrinkage and Lévy Processes
Paper and Code
Jan 11, 2014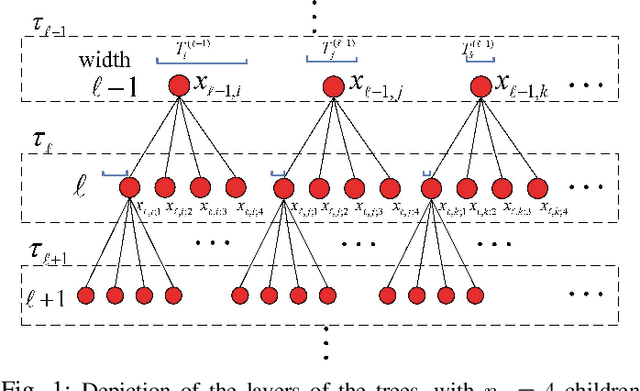
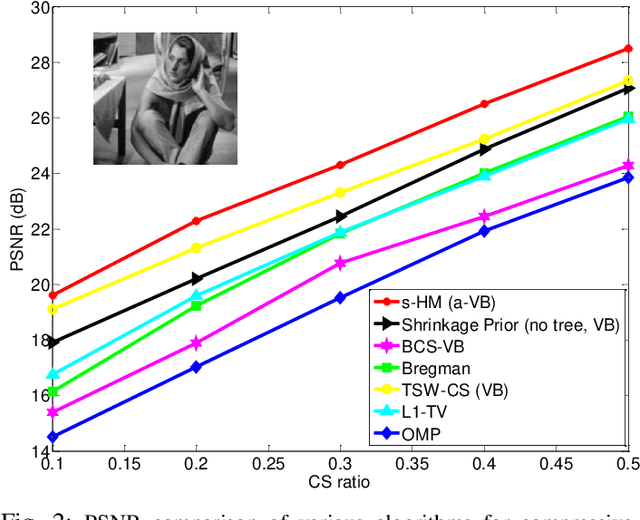
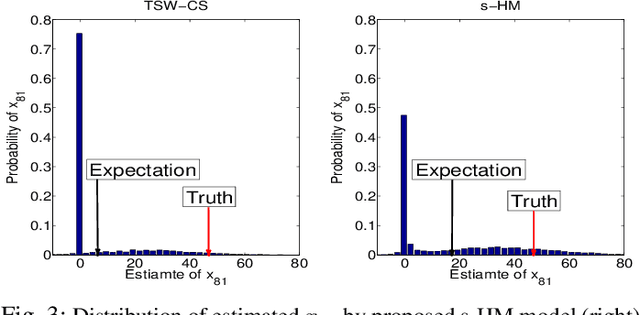
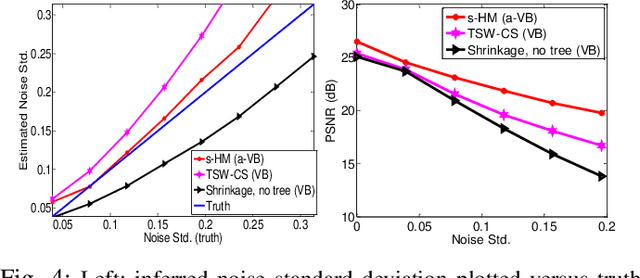
A new shrinkage-based construction is developed for a compressible vector $\boldsymbol{x}\in\mathbb{R}^n$, for cases in which the components of $\xv$ are naturally associated with a tree structure. Important examples are when $\xv$ corresponds to the coefficients of a wavelet or block-DCT representation of data. The method we consider in detail, and for which numerical results are presented, is based on increments of a gamma process. However, we demonstrate that the general framework is appropriate for many other types of shrinkage priors, all within the L\'{e}vy process family, with the gamma process a special case. Bayesian inference is carried out by approximating the posterior with samples from an MCMC algorithm, as well as by constructing a heuristic variational approximation to the posterior. We also consider expectation-maximization (EM) for a MAP (point) solution. State-of-the-art results are manifested for compressive sensing and denoising applications, the latter with spiky (non-Gaussian) noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge