VB-LoRA: Extreme Parameter Efficient Fine-Tuning with Vector Banks

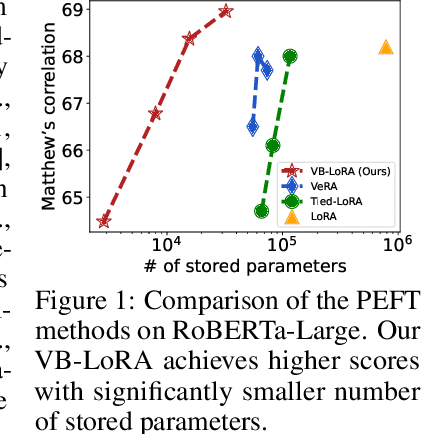
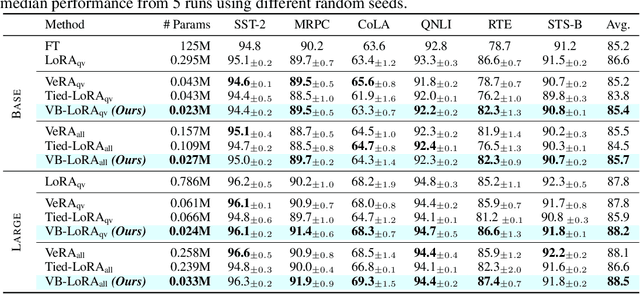
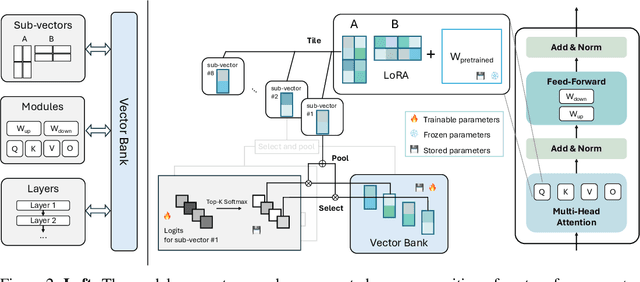
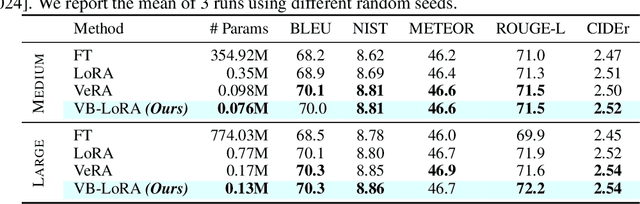
As the adoption of large language models increases and the need for per-user or per-task model customization grows, the parameter-efficient fine-tuning (PEFT) methods, such as low-rank adaptation (LoRA) and its variants, incur substantial storage and transmission costs. To further reduce stored parameters, we introduce a "divide-and-share" paradigm that breaks the barriers of low-rank decomposition across matrix dimensions, modules and layers by sharing parameters globally via a vector bank. As an instantiation of the paradigm to LoRA, our proposed VB-LoRA composites all the low-rank matrices of LoRA from a shared vector bank with a differentiable top-$k$ admixture module. VB-LoRA achieves extreme parameter efficiency while maintaining comparable or better performance compared to state-of-the-art PEFT methods. Extensive experiments demonstrate the effectiveness of VB-LoRA on natural language understanding, natural language generation, and instruction tuning tasks. When fine-tuning the Llama2-13B model, VB-LoRA only uses 0.4% of LoRA's stored parameters, yet achieves superior results. Our source code is available at https://github.com/leo-yangli/VB-LoRA.

Exploring Compositional Visual Generation with Latent Classifier Guidance

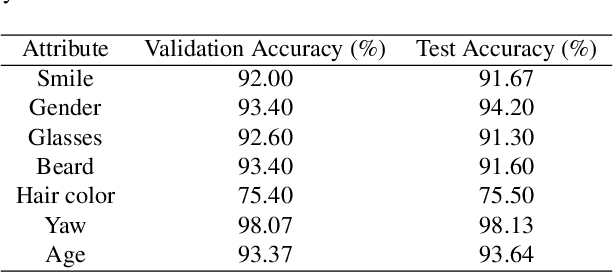
Diffusion probabilistic models have achieved enormous success in the field of image generation and manipulation. In this paper, we explore a novel paradigm of using the diffusion model and classifier guidance in the latent semantic space for compositional visual tasks. linear fashion. Specifically, we train latent diffusion models and auxiliary latent classifiers to facilitate non-linear navigation of latent representation generation for any pre-trained generative model with a semantic latent space. We demonstrate that such conditional generation achieved by latent classifier guidance provably maximizes a lower bound of the conditional log probability during training. To maintain the original semantics during manipulation, we introduce a new guidance term, which we show is crucial for achieving compositionality. With additional assumptions, we show that the non-linear manipulation reduces to a simple latent arithmetic approach. We show that this paradigm based on latent classifier guidance is agnostic to pre-trained generative models, and present competitive results for both image generation and sequential manipulation of real and synthetic images. Our findings suggest that latent classifier guidance is a promising approach that merits further exploration, even in the presence of other strong competing methods.

Learning Transferable Reward for Query Object Localization with Policy Adaptation

We propose a reinforcement learning based approach to query object localization, for which an agent is trained to localize objects of interest specified by a small exemplary set. We learn a transferable reward signal formulated using the exemplary set by ordinal metric learning. Our proposed method enables test-time policy adaptation to new environments where the reward signals are not readily available, and outperforms fine-tuning approaches that are limited to annotated images. In addition, the transferable reward allows repurposing the trained agent from one specific class to another class. Experiments on corrupted MNIST, CU-Birds, and COCO datasets demonstrate the effectiveness of our approach.

Provable Adaptation across Multiway Domains via Representation Learning

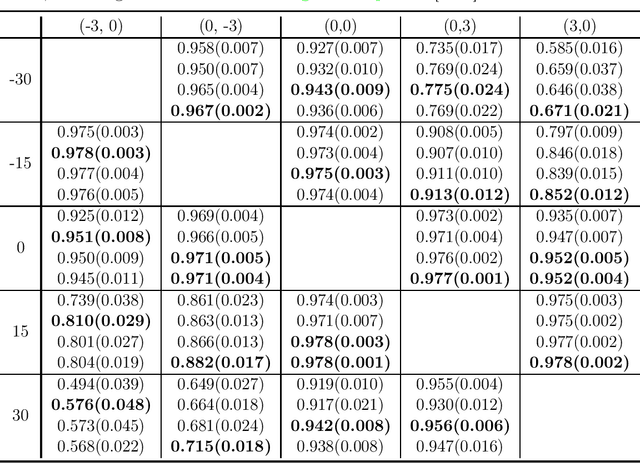
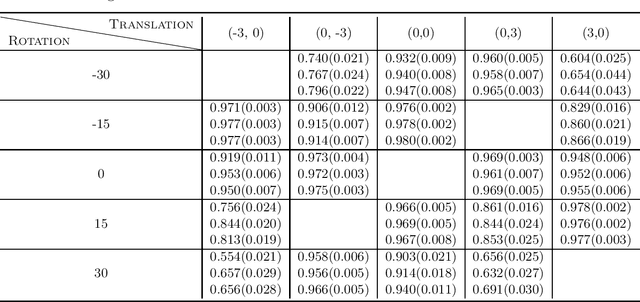
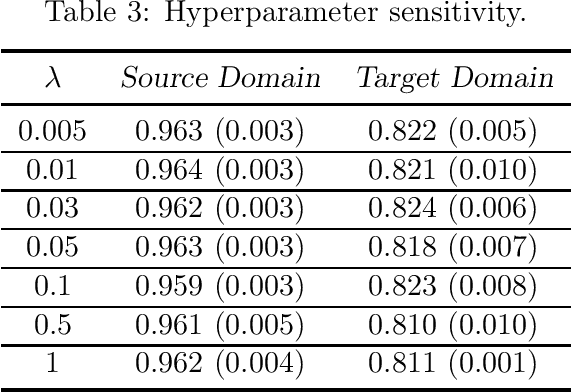
This paper studies zero-shot domain adaptation where each domain is indexed on a multi-dimensional array, and we only have data from a small subset of domains. Our goal is to produce predictors that perform well on \emph{unseen} domains. We propose a model which consists of a domain-invariant latent representation layer and a domain-specific linear prediction layer with a low-rank tensor structure. Theoretically, we present explicit sample complexity bounds to characterize the prediction error on unseen domains in terms of the number of domains with training data and the number of data per domain. To our knowledge, this is the first finite-sample guarantee for zero-shot domain adaptation. In addition, we provide experiments on two-way MNIST and four-way fiber sensing datasets to demonstrate the effectiveness of our proposed model.

Supervised Coarse-Graining of Composite Objects

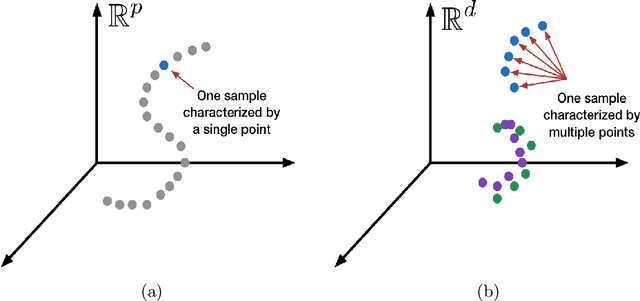
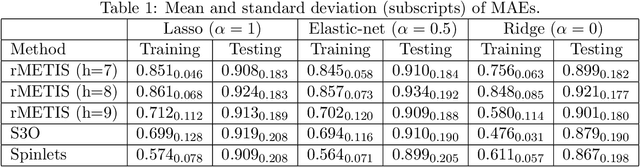
We consider supervised dimension reduction for regression with composite object-valued predictors, which are composed of primitive variables located on an underlying relevant space. For example, this type of predictor can refer to a number of time-stamped events or a collection of interactions between units indexed by spatial coordinates. To facilitate regression analysis on such data, it is desirable to reduce the complex object into a malleable vector form with a tradeoff between homogeneity and heterogeneity. In this article, we introduce a tree-guided supervised dimension reduction method, called multiscale coarse-graining, that uses the similarity among primitive variables for deriving a part-subpart hierarchical representation of the composite object, and chooses non-uniform resolutions according to the relevance to the response. We propose a multiscale extension of the generalized double Pareto prior based on parameter expansion, which induces simultaneous deletion and fusion of the primitive variables through adaptive shrinkage estimation. We demonstrate the practical utility of our approach with an application in soccer analytics, in which we obtain coarse-grained visualizations of spatial passing networks under the supervision of team performance.

Multiresolution Tensor Decomposition for Multiple Spatial Passing Networks

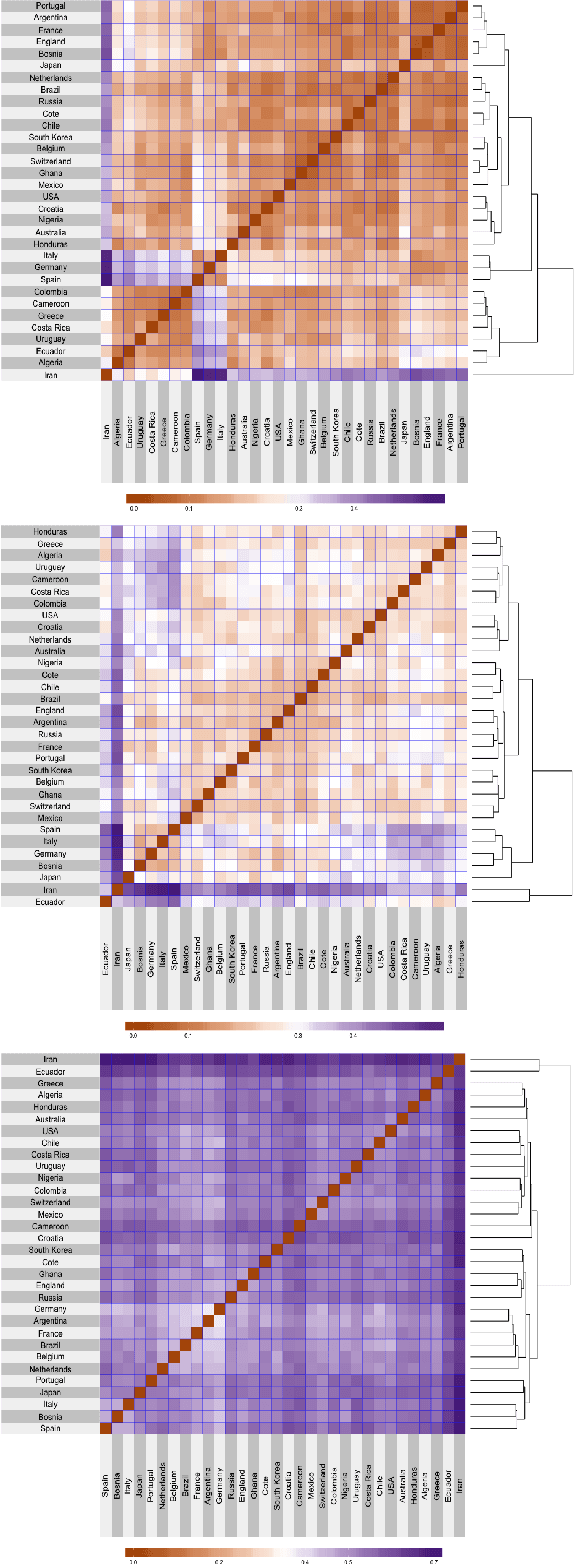
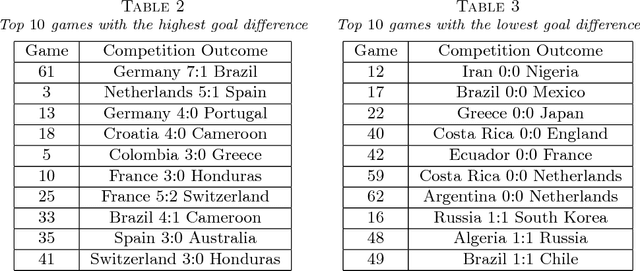
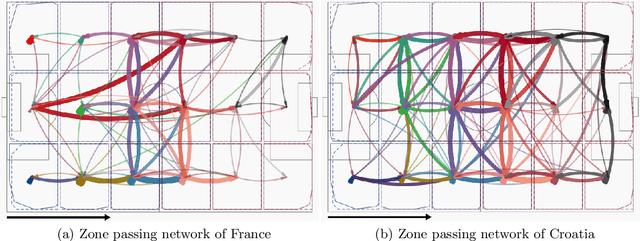
This article is motivated by soccer positional passing networks collected across multiple games. We refer to these data as replicated spatial passing networks---to accurately model such data it is necessary to take into account the spatial positions of the passer and receiver for each passing event. This spatial registration and replicates that occur across games represent key differences with usual social network data. As a key step before investigating how the passing dynamics influence team performance, we focus on developing methods for summarizing different team's passing strategies. Our proposed approach relies on a novel multiresolution data representation framework and Poisson nonnegative block term decomposition model, which automatically produces coarse-to-fine low-rank network motifs. The proposed methods are applied to detailed passing record data collected from the 2014 FIFA World Cup.

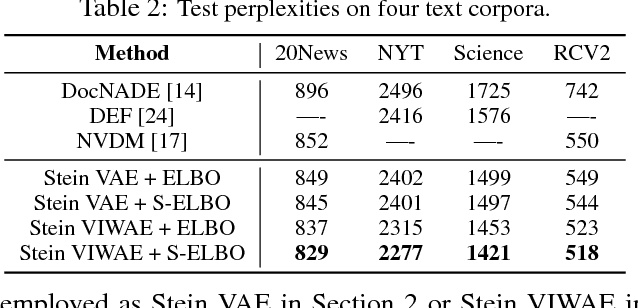
VAE Learning via Stein Variational Gradient Descent

A new method for learning variational autoencoders (VAEs) is developed, based on Stein variational gradient descent. A key advantage of this approach is that one need not make parametric assumptions about the form of the encoder distribution. Performance is further enhanced by integrating the proposed encoder with importance sampling. Excellent performance is demonstrated across multiple unsupervised and semi-supervised problems, including semi-supervised analysis of the ImageNet data, demonstrating the scalability of the model to large datasets.

Variational Gaussian Copula Inference

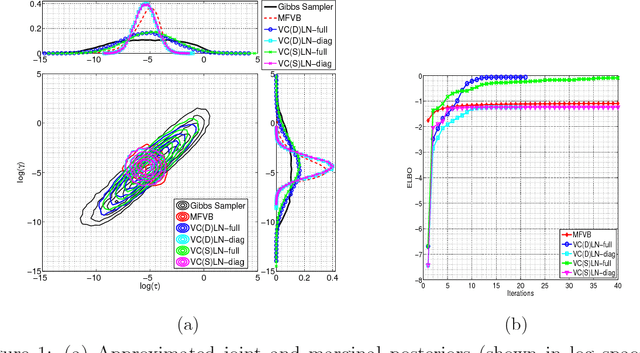
We utilize copulas to constitute a unified framework for constructing and optimizing variational proposals in hierarchical Bayesian models. For models with continuous and non-Gaussian hidden variables, we propose a semiparametric and automated variational Gaussian copula approach, in which the parametric Gaussian copula family is able to preserve multivariate posterior dependence, and the nonparametric transformations based on Bernstein polynomials provide ample flexibility in characterizing the univariate marginal posteriors.

Alternating Minimization Algorithm with Automatic Relevance Determination for Transmission Tomography under Poisson Noise

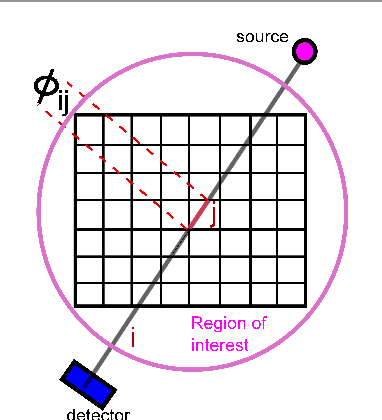
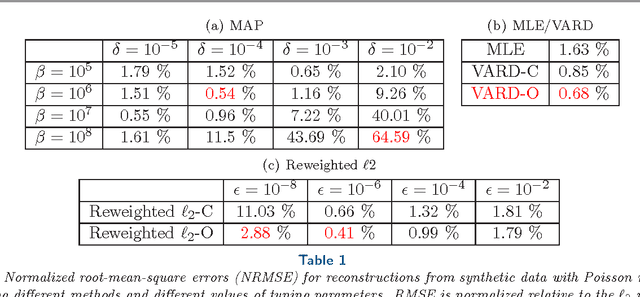
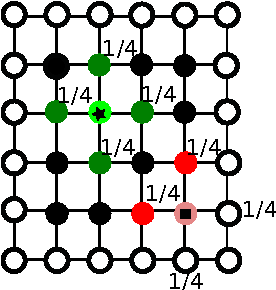
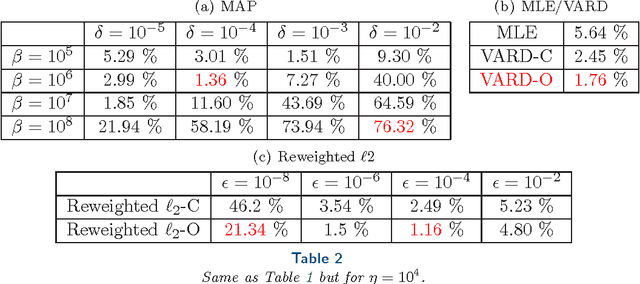
We propose a globally convergent alternating minimization (AM) algorithm for image reconstruction in transmission tomography, which extends automatic relevance determination (ARD) to Poisson noise models with Beer's law. The algorithm promotes solutions that are sparse in the pixel/voxel-differences domain by introducing additional latent variables, one for each pixel/voxel, and then learning these variables from the data using a hierarchical Bayesian model. Importantly, the proposed AM algorithm is free of any tuning parameters with image quality comparable to standard penalized likelihood methods. Our algorithm exploits optimization transfer principles which reduce the problem into parallel 1D optimization tasks (one for each pixel/voxel), making the algorithm feasible for large-scale problems. This approach considerably reduces the computational bottleneck of ARD associated with the posterior variances. Positivity constraints inherent in transmission tomography problems are also enforced. We demonstrate the performance of the proposed algorithm for x-ray computed tomography using synthetic and real-world datasets. The algorithm is shown to have much better performance than prior ARD algorithms based on approximate Gaussian noise models, even for high photon flux.

Multiscale Shrinkage and Lévy Processes

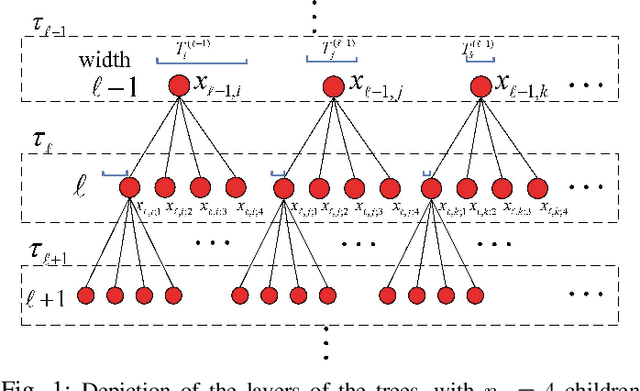
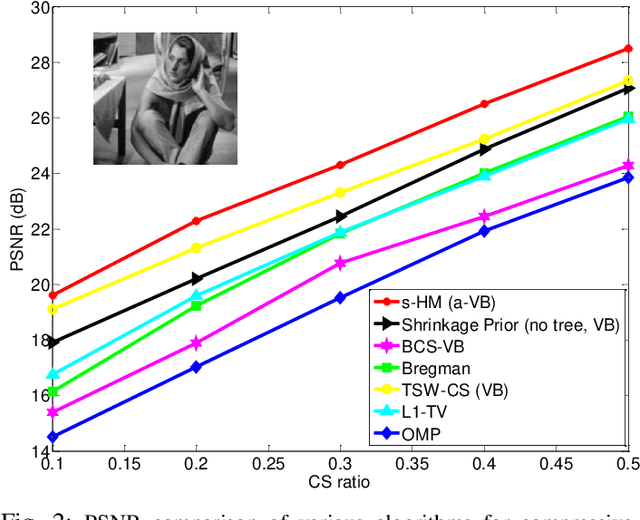
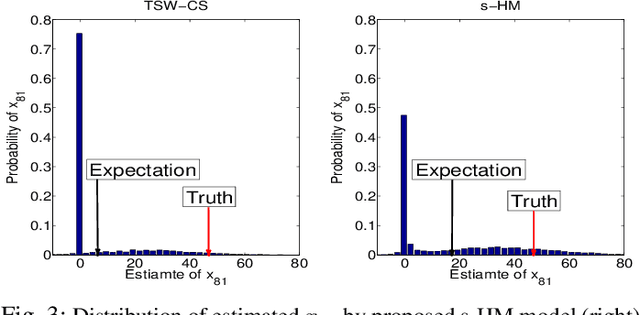
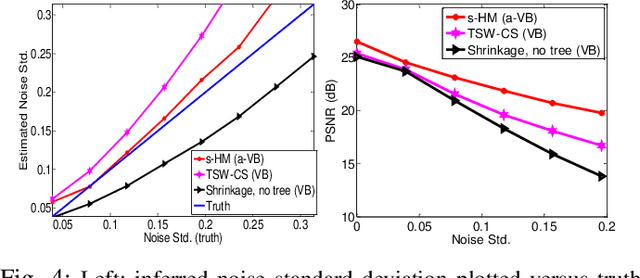
A new shrinkage-based construction is developed for a compressible vector $\boldsymbol{x}\in\mathbb{R}^n$, for cases in which the components of $\xv$ are naturally associated with a tree structure. Important examples are when $\xv$ corresponds to the coefficients of a wavelet or block-DCT representation of data. The method we consider in detail, and for which numerical results are presented, is based on increments of a gamma process. However, we demonstrate that the general framework is appropriate for many other types of shrinkage priors, all within the L\'{e}vy process family, with the gamma process a special case. Bayesian inference is carried out by approximating the posterior with samples from an MCMC algorithm, as well as by constructing a heuristic variational approximation to the posterior. We also consider expectation-maximization (EM) for a MAP (point) solution. State-of-the-art results are manifested for compressive sensing and denoising applications, the latter with spiky (non-Gaussian) noise.