Provable Adaptation across Multiway Domains via Representation Learning
Paper and Code
Jun 12, 2021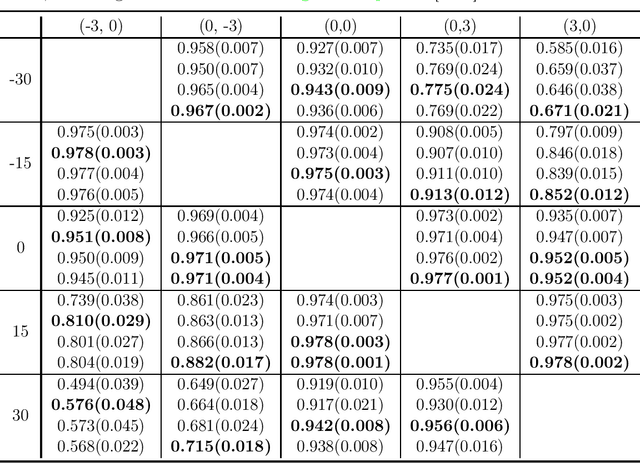

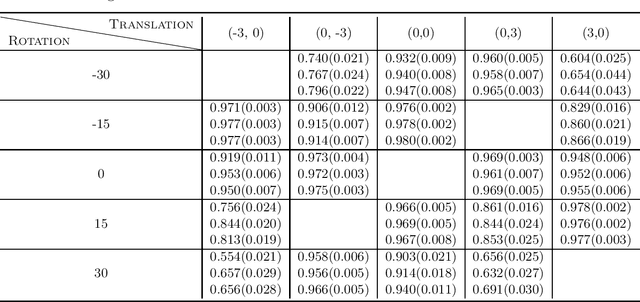
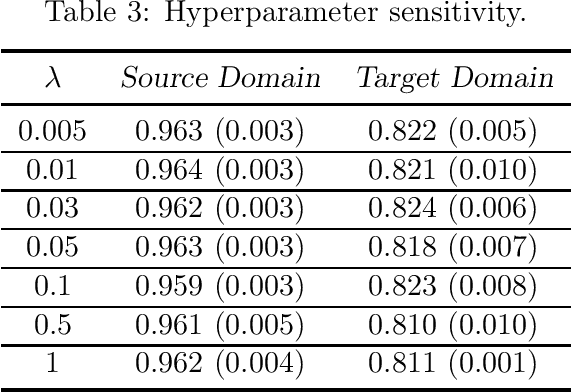
This paper studies zero-shot domain adaptation where each domain is indexed on a multi-dimensional array, and we only have data from a small subset of domains. Our goal is to produce predictors that perform well on \emph{unseen} domains. We propose a model which consists of a domain-invariant latent representation layer and a domain-specific linear prediction layer with a low-rank tensor structure. Theoretically, we present explicit sample complexity bounds to characterize the prediction error on unseen domains in terms of the number of domains with training data and the number of data per domain. To our knowledge, this is the first finite-sample guarantee for zero-shot domain adaptation. In addition, we provide experiments on two-way MNIST and four-way fiber sensing datasets to demonstrate the effectiveness of our proposed model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge