A Probabilistic Framework for Nonlinearities in Stochastic Neural Networks

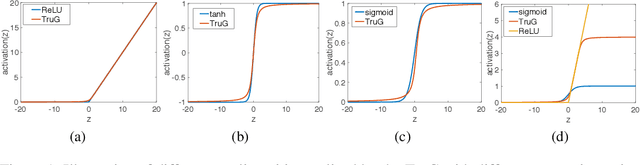
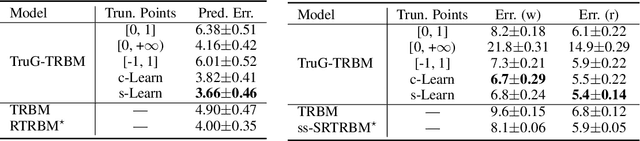
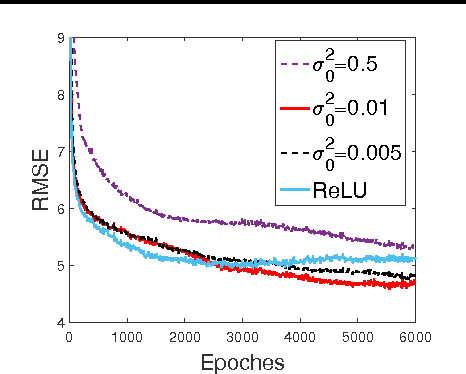
We present a probabilistic framework for nonlinearities, based on doubly truncated Gaussian distributions. By setting the truncation points appropriately, we are able to generate various types of nonlinearities within a unified framework, including sigmoid, tanh and ReLU, the most commonly used nonlinearities in neural networks. The framework readily integrates into existing stochastic neural networks (with hidden units characterized as random variables), allowing one for the first time to learn the nonlinearities alongside model weights in these networks. Extensive experiments demonstrate the performance improvements brought about by the proposed framework when integrated with the restricted Boltzmann machine (RBM), temporal RBM and the truncated Gaussian graphical model (TGGM).

Nonlinear Statistical Learning with Truncated Gaussian Graphical Models

We introduce the truncated Gaussian graphical model (TGGM) as a novel framework for designing statistical models for nonlinear learning. A TGGM is a Gaussian graphical model (GGM) with a subset of variables truncated to be nonnegative. The truncated variables are assumed latent and integrated out to induce a marginal model. We show that the variables in the marginal model are non-Gaussian distributed and their expected relations are nonlinear. We use expectation-maximization to break the inference of the nonlinear model into a sequence of TGGM inference problems, each of which is efficiently solved by using the properties and numerical methods of multivariate Gaussian distributions. We use the TGGM to design models for nonlinear regression and classification, with the performances of these models demonstrated on extensive benchmark datasets and compared to state-of-the-art competing results.

Unsupervised Learning with Truncated Gaussian Graphical Models

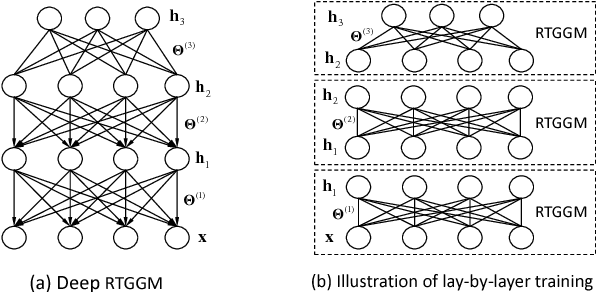
Gaussian graphical models (GGMs) are widely used for statistical modeling, because of ease of inference and the ubiquitous use of the normal distribution in practical approximations. However, they are also known for their limited modeling abilities, due to the Gaussian assumption. In this paper, we introduce a novel variant of GGMs, which relaxes the Gaussian restriction and yet admits efficient inference. Specifically, we impose a bipartite structure on the GGM and govern the hidden variables by truncated normal distributions. The nonlinearity of the model is revealed by its connection to rectified linear unit (ReLU) neural networks. Meanwhile, thanks to the bipartite structure and appealing properties of truncated normals, we are able to train the models efficiently using contrastive divergence. We consider three output constructs, accounting for real-valued, binary and count data. We further extend the model to deep constructions and show that deep models can be used for unsupervised pre-training of rectifier neural networks. Extensive experimental results are provided to validate the proposed models and demonstrate their superiority over competing models.

Variational Gaussian Copula Inference

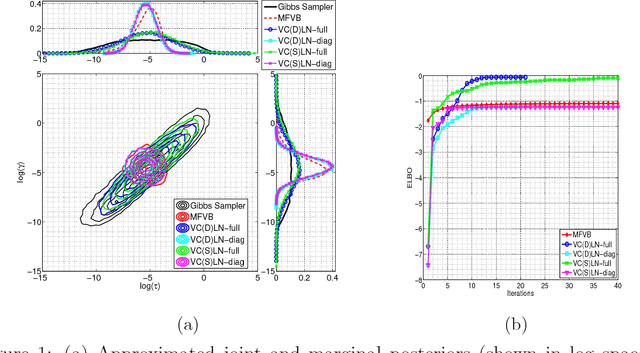
We utilize copulas to constitute a unified framework for constructing and optimizing variational proposals in hierarchical Bayesian models. For models with continuous and non-Gaussian hidden variables, we propose a semiparametric and automated variational Gaussian copula approach, in which the parametric Gaussian copula family is able to preserve multivariate posterior dependence, and the nonparametric transformations based on Bernstein polynomials provide ample flexibility in characterizing the univariate marginal posteriors.

Stick-Breaking Policy Learning in Dec-POMDPs

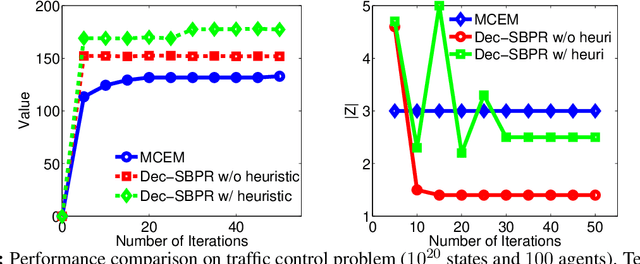
Expectation maximization (EM) has recently been shown to be an efficient algorithm for learning finite-state controllers (FSCs) in large decentralized POMDPs (Dec-POMDPs). However, current methods use fixed-size FSCs and often converge to maxima that are far from optimal. This paper considers a variable-size FSC to represent the local policy of each agent. These variable-size FSCs are constructed using a stick-breaking prior, leading to a new framework called \emph{decentralized stick-breaking policy representation} (Dec-SBPR). This approach learns the controller parameters with a variational Bayesian algorithm without having to assume that the Dec-POMDP model is available. The performance of Dec-SBPR is demonstrated on several benchmark problems, showing that the algorithm scales to large problems while outperforming other state-of-the-art methods.

Low-Cost Compressive Sensing for Color Video and Depth

A simple and inexpensive (low-power and low-bandwidth) modification is made to a conventional off-the-shelf color video camera, from which we recover {multiple} color frames for each of the original measured frames, and each of the recovered frames can be focused at a different depth. The recovery of multiple frames for each measured frame is made possible via high-speed coding, manifested via translation of a single coded aperture; the inexpensive translation is constituted by mounting the binary code on a piezoelectric device. To simultaneously recover depth information, a {liquid} lens is modulated at high speed, via a variable voltage. Consequently, during the aforementioned coding process, the liquid lens allows the camera to sweep the focus through multiple depths. In addition to designing and implementing the camera, fast recovery is achieved by an anytime algorithm exploiting the group-sparsity of wavelet/DCT coefficients.

Adaptive Temporal Compressive Sensing for Video

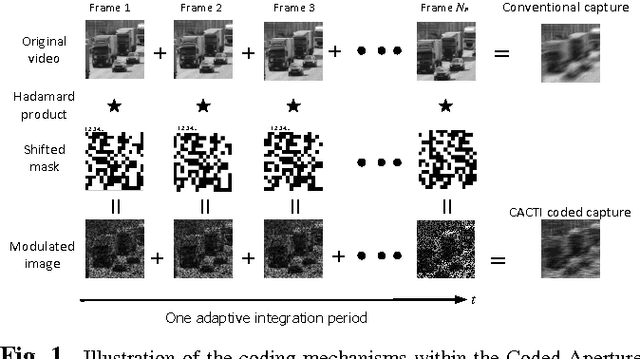
This paper introduces the concept of adaptive temporal compressive sensing (CS) for video. We propose a CS algorithm to adapt the compression ratio based on the scene's temporal complexity, computed from the compressed data, without compromising the quality of the reconstructed video. The temporal adaptivity is manifested by manipulating the integration time of the camera, opening the possibility to real-time implementation. The proposed algorithm is a generalized temporal CS approach that can be incorporated with a diverse set of existing hardware systems.

Coded aperture compressive temporal imaging

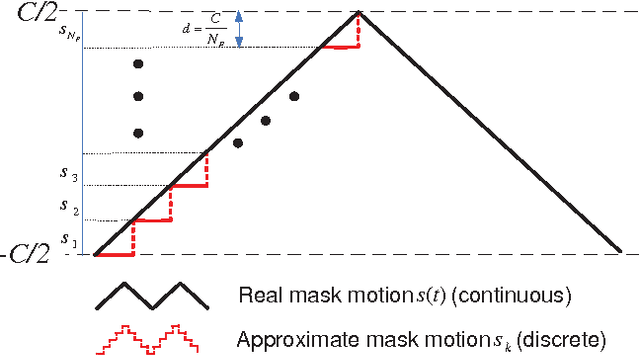
We use mechanical translation of a coded aperture for code division multiple access compression of video. We present experimental results for reconstruction at 148 frames per coded snapshot.

Cross-Domain Multitask Learning with Latent Probit Models

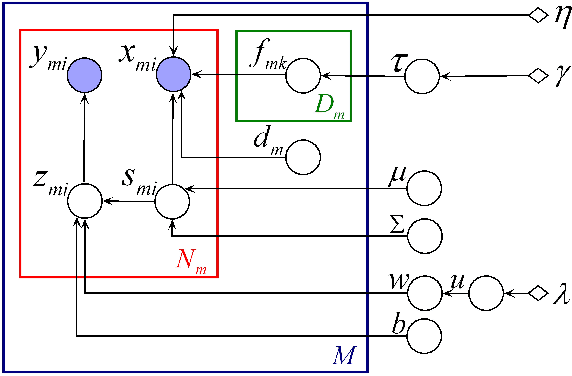
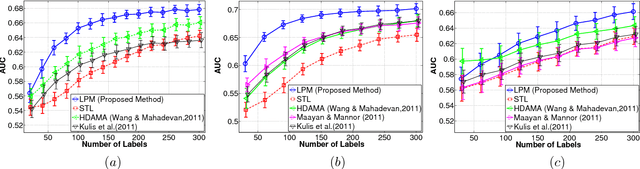
Learning multiple tasks across heterogeneous domains is a challenging problem since the feature space may not be the same for different tasks. We assume the data in multiple tasks are generated from a latent common domain via sparse domain transforms and propose a latent probit model (LPM) to jointly learn the domain transforms, and the shared probit classifier in the common domain. To learn meaningful task relatedness and avoid over-fitting in classification, we introduce sparsity in the domain transforms matrices, as well as in the common classifier. We derive theoretical bounds for the estimation error of the classifier in terms of the sparsity of domain transforms. An expectation-maximization algorithm is derived for learning the LPM. The effectiveness of the approach is demonstrated on several real datasets.