Nonlinear Statistical Learning with Truncated Gaussian Graphical Models
Paper and Code
Nov 20, 2016

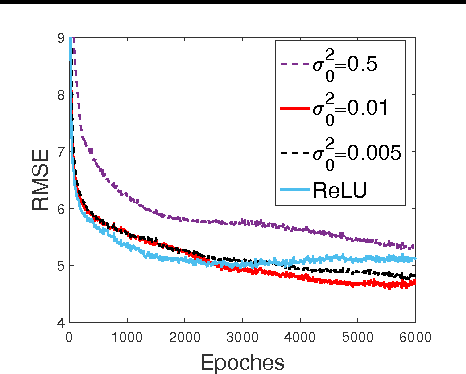

We introduce the truncated Gaussian graphical model (TGGM) as a novel framework for designing statistical models for nonlinear learning. A TGGM is a Gaussian graphical model (GGM) with a subset of variables truncated to be nonnegative. The truncated variables are assumed latent and integrated out to induce a marginal model. We show that the variables in the marginal model are non-Gaussian distributed and their expected relations are nonlinear. We use expectation-maximization to break the inference of the nonlinear model into a sequence of TGGM inference problems, each of which is efficiently solved by using the properties and numerical methods of multivariate Gaussian distributions. We use the TGGM to design models for nonlinear regression and classification, with the performances of these models demonstrated on extensive benchmark datasets and compared to state-of-the-art competing results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge