Stick-Breaking Policy Learning in Dec-POMDPs
Paper and Code
Nov 23, 2015


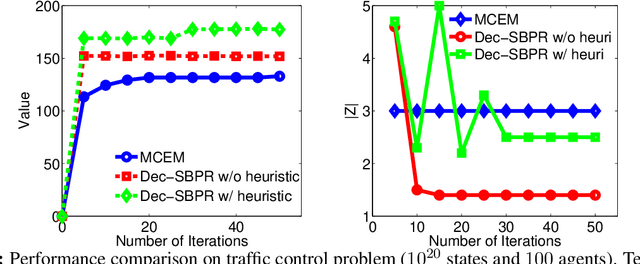
Expectation maximization (EM) has recently been shown to be an efficient algorithm for learning finite-state controllers (FSCs) in large decentralized POMDPs (Dec-POMDPs). However, current methods use fixed-size FSCs and often converge to maxima that are far from optimal. This paper considers a variable-size FSC to represent the local policy of each agent. These variable-size FSCs are constructed using a stick-breaking prior, leading to a new framework called \emph{decentralized stick-breaking policy representation} (Dec-SBPR). This approach learns the controller parameters with a variational Bayesian algorithm without having to assume that the Dec-POMDP model is available. The performance of Dec-SBPR is demonstrated on several benchmark problems, showing that the algorithm scales to large problems while outperforming other state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge