Supervised Coarse-Graining of Composite Objects
Paper and Code
Jan 01, 2019
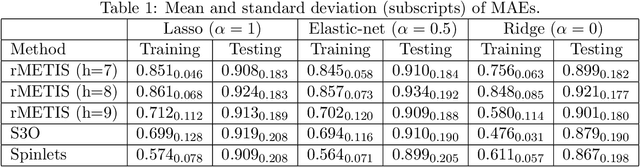

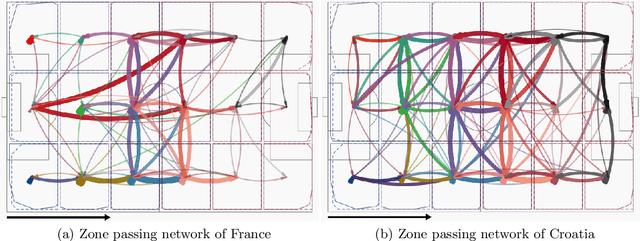
We consider supervised dimension reduction for regression with composite object-valued predictors, which are composed of primitive variables located on an underlying relevant space. For example, this type of predictor can refer to a number of time-stamped events or a collection of interactions between units indexed by spatial coordinates. To facilitate regression analysis on such data, it is desirable to reduce the complex object into a malleable vector form with a tradeoff between homogeneity and heterogeneity. In this article, we introduce a tree-guided supervised dimension reduction method, called multiscale coarse-graining, that uses the similarity among primitive variables for deriving a part-subpart hierarchical representation of the composite object, and chooses non-uniform resolutions according to the relevance to the response. We propose a multiscale extension of the generalized double Pareto prior based on parameter expansion, which induces simultaneous deletion and fusion of the primitive variables through adaptive shrinkage estimation. We demonstrate the practical utility of our approach with an application in soccer analytics, in which we obtain coarse-grained visualizations of spatial passing networks under the supervision of team performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge