MB-DECTNet: A Model-Based Unrolled Network for Accurate 3D DECT Reconstruction

Numerous dual-energy CT (DECT) techniques have been developed in the past few decades. Dual-energy CT (DECT) statistical iterative reconstruction (SIR) has demonstrated its potential for reducing noise and increasing accuracy. Our lab proposed a joint statistical DECT algorithm for stopping power estimation and showed that it outperforms competing image-based material-decomposition methods. However, due to its slow convergence and the high computational cost of projections, the elapsed time of 3D DECT SIR is often not clinically acceptable. Therefore, to improve its convergence, we have embedded DECT SIR into a deep learning model-based unrolled network for 3D DECT reconstruction (MB-DECTNet) that can be trained in an end-to-end fashion. This deep learning-based method is trained to learn the shortcuts between the initial conditions and the stationary points of iterative algorithms while preserving the unbiased estimation property of model-based algorithms. MB-DECTNet is formed by stacking multiple update blocks, each of which consists of a data consistency layer (DC) and a spatial mixer layer, where the spatial mixer layer is the shrunken U-Net, and the DC layer is a one-step update of an arbitrary traditional iterative method. Although the proposed network can be combined with numerous iterative DECT algorithms, we demonstrate its performance with the dual-energy alternating minimization (DEAM). The qualitative result shows that MB-DECTNet with DEAM significantly reduces noise while increasing the resolution of the test image. The quantitative result shows that MB-DECTNet has the potential to estimate attenuation coefficients accurately as traditional statistical algorithms but with a much lower computational cost.

A Metal Artifact Reduction Scheme For Accurate Iterative Dual-Energy CT Algorithms

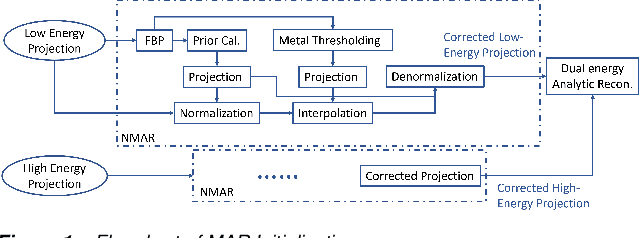
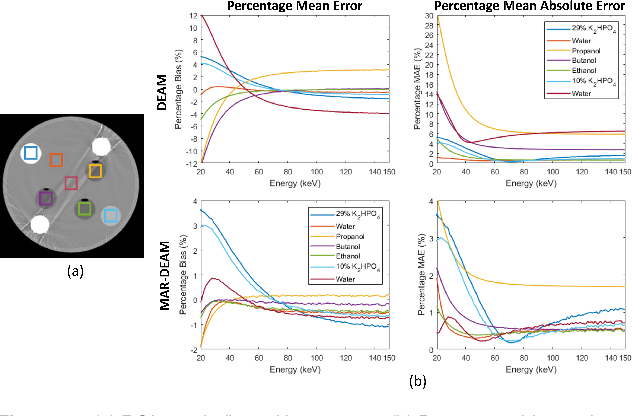
CT images have been used to generate radiation therapy treatment plans for more than two decades. Dual-energy CT (DECT) has shown high accuracy in estimating electronic density or proton stopping-power maps used in treatment planning. However, the presence of metal implants introduces severe streaking artifacts in the reconstructed images, affecting the diagnostic accuracy and treatment performance. In order to reduce the metal artifacts in DECT, we introduce a metal-artifact reduction scheme for iterative DECT algorithms. An estimate is substituted for the corrupt data in each iteration. We utilize normalized metal-artifact reduction (NMAR) composed with image-domain decomposition to initialize the algorithm and speed up the convergence. A fully 3D joint statistical DECT algorithm, dual-energy alternating minimization (DEAM), with the proposed scheme is tested on experimental and clinical helical data acquired on a Philips Brilliance Big Bore scanner. We compared DEAM with the proposed method to the original DEAM and vendor reconstructions with and without metal-artifact reduction for orthopedic implants (O-MAR). The visualization and quantitative analysis show that DEAM with the proposed method has the best performance in reducing streaking artifacts caused by metallic objects.

A Machine-learning Based Initialization for Joint Statistical Iterative Dual-energy CT with Application to Proton Therapy

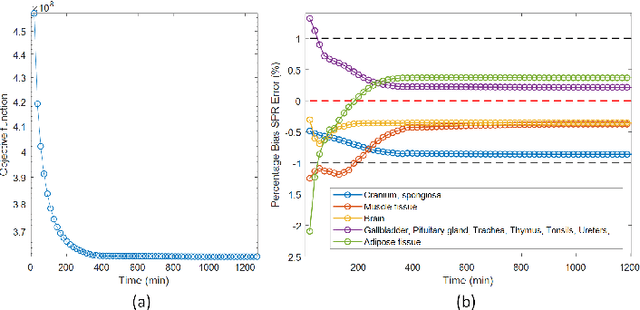
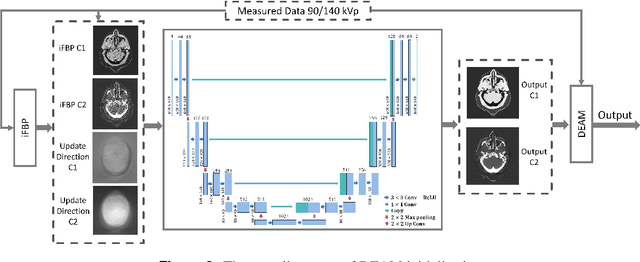
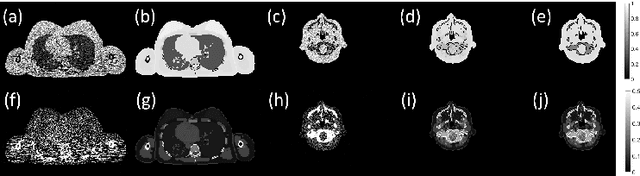
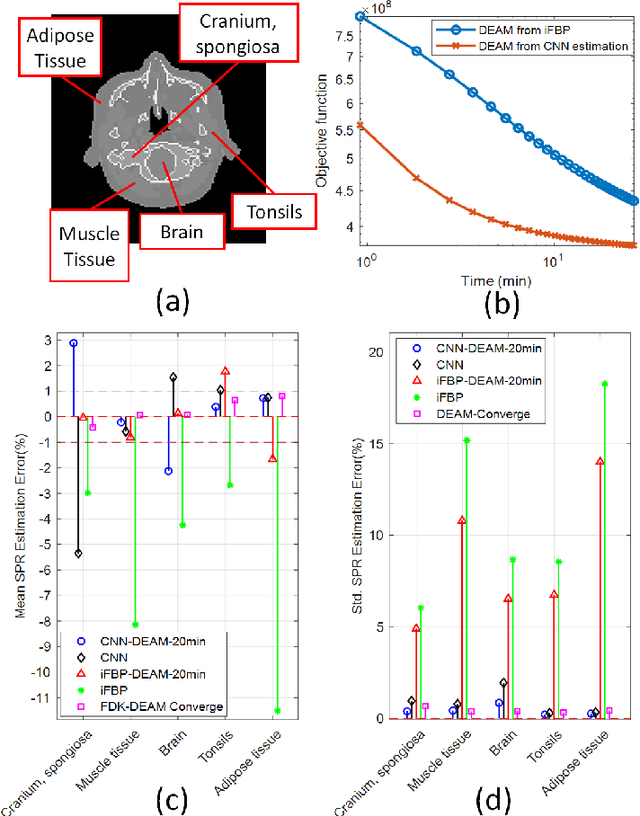
Dual-energy CT (DECT) has been widely investigated to generate more informative and more accurate images in the past decades. For example, Dual-Energy Alternating Minimization (DEAM) algorithm achieves sub-percentage uncertainty in estimating proton stopping-power mappings from experimental 3-mm collimated phantom data. However, elapsed time of iterative DECT algorithms is not clinically acceptable, due to their low convergence rate and the tremendous geometry of modern helical CT scanners. A CNN-based initialization method is introduced to reduce the computational time of iterative DECT algorithms. DEAM is used as an example of iterative DECT algorithms in this work. The simulation results show that our method generates denoised images with greatly improved estimation accuracy for adipose, tonsils, and muscle tissue. Also, it reduces elapsed time by approximately 5-fold for DEAM to reach the same objective function value for both simulated and real data.

Highly accurate model for prediction of lung nodule malignancy with CT scans

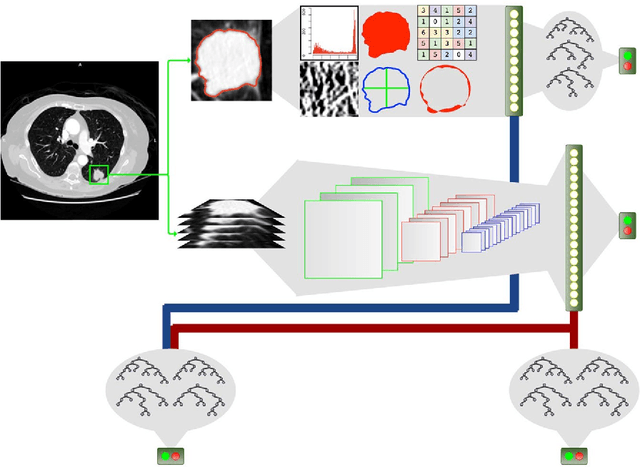
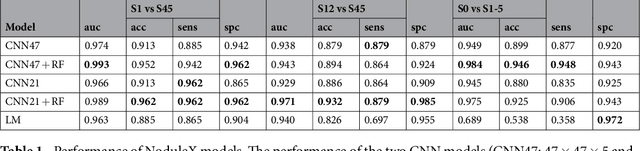
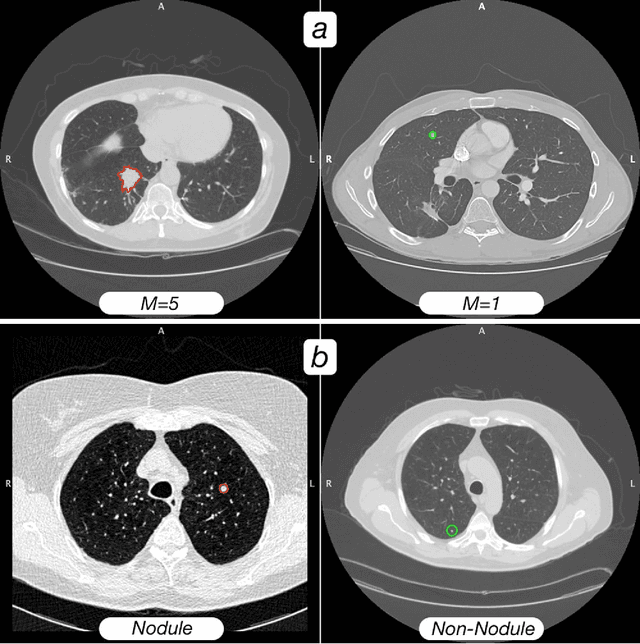
Computed tomography (CT) examinations are commonly used to predict lung nodule malignancy in patients, which are shown to improve noninvasive early diagnosis of lung cancer. It remains challenging for computational approaches to achieve performance comparable to experienced radiologists. Here we present NoduleX, a systematic approach to predict lung nodule malignancy from CT data, based on deep learning convolutional neural networks (CNN). For training and validation, we analyze >1000 lung nodules in images from the LIDC/IDRI cohort. All nodules were identified and classified by four experienced thoracic radiologists who participated in the LIDC project. NoduleX achieves high accuracy for nodule malignancy classification, with an AUC of ~0.99. This is commensurate with the analysis of the dataset by experienced radiologists. Our approach, NoduleX, provides an effective framework for highly accurate nodule malignancy prediction with the model trained on a large patient population. Our results are replicable with software available at http://bioinformatics.astate.edu/NoduleX.

Laplacian Prior Variational Automatic Relevance Determination for Transmission Tomography

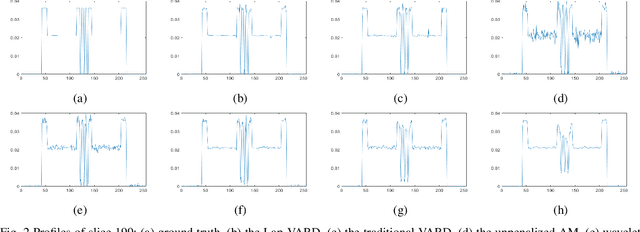
In the classic sparsity-driven problems, the fundamental L-1 penalty method has been shown to have good performance in reconstructing signals for a wide range of problems. However this performance relies on a good choice of penalty weight which is often found from empirical experiments. We propose an algorithm called the Laplacian variational automatic relevance determination (Lap-VARD) that takes this penalty weight as a parameter of a prior Laplace distribution. Optimization of this parameter using an automatic relevance determination framework results in a balance between the sparsity and accuracy of signal reconstruction. Our algorithm is implemented in a transmission tomography model with sparsity constraint in wavelet domain.

Spectrally Grouped Total Variation Reconstruction for Scatter Imaging Using ADMM

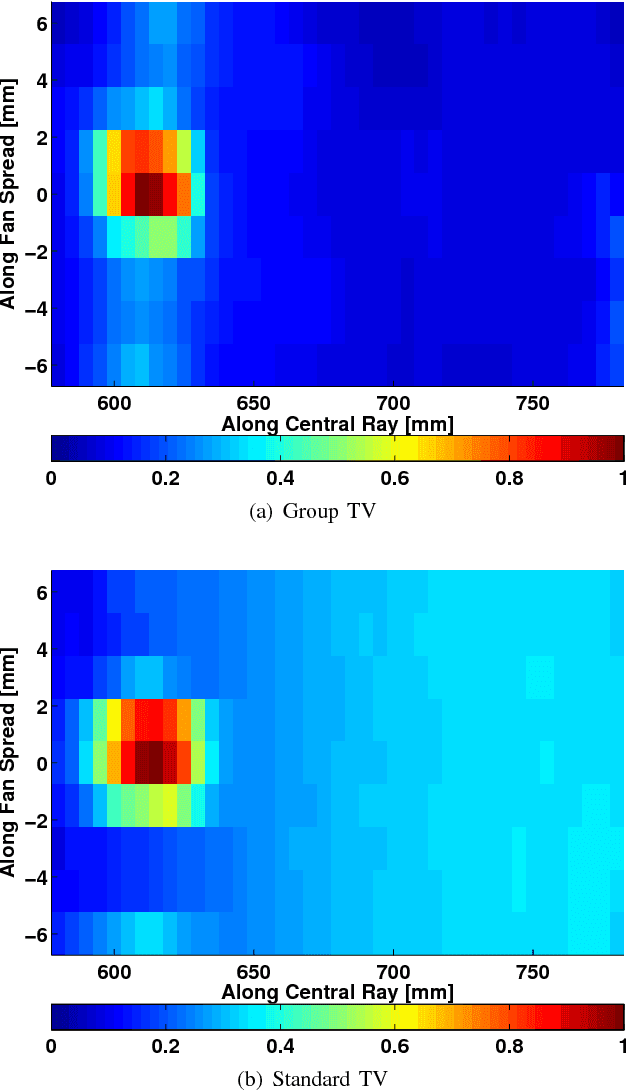
We consider X-ray coherent scatter imaging, where the goal is to reconstruct momentum transfer profiles (spectral distributions) at each spatial location from multiplexed measurements of scatter. Each material is characterized by a unique momentum transfer profile (MTP) which can be used to discriminate between different materials. We propose an iterative image reconstruction algorithm based on a Poisson noise model that can account for photon-limited measurements as well as various second order statistics of the data. To improve image quality, previous approaches use edge-preserving regularizers to promote piecewise constancy of the image in the spatial domain while treating each spectral bin separately. Instead, we propose spectrally grouped regularization that promotes piecewise constant images along the spatial directions but also ensures that the MTPs of neighboring spatial bins are similar, if they contain the same material. We demonstrate that this group regularization results in improvement of both spectral and spatial image quality. We pursue an optimization transfer approach where convex decompositions are used to lift the problem such that all hyper-voxels can be updated in parallel and in closed-form. The group penalty introduces a challenge since it is not directly amendable to these decompositions. We use the alternating directions method of multipliers (ADMM) to replace the original problem with an equivalent sequence of sub-problems that are amendable to convex decompositions, leading to a highly parallel algorithm. We demonstrate the performance on real data.

Joint System and Algorithm Design for Computationally Efficient Fan Beam Coded Aperture X-ray Coherent Scatter Imaging

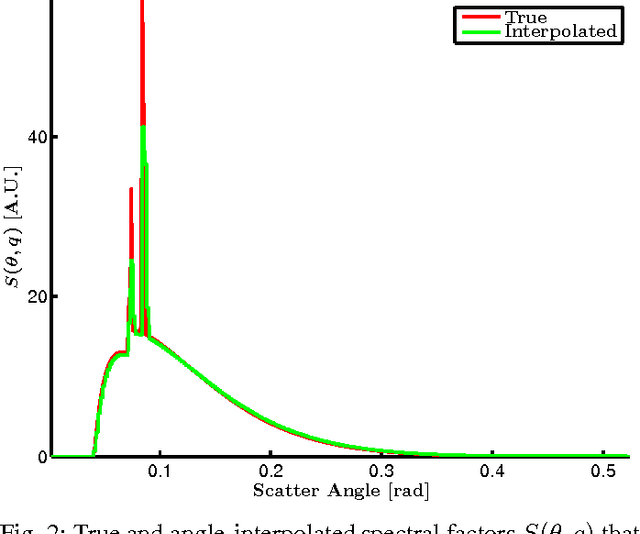
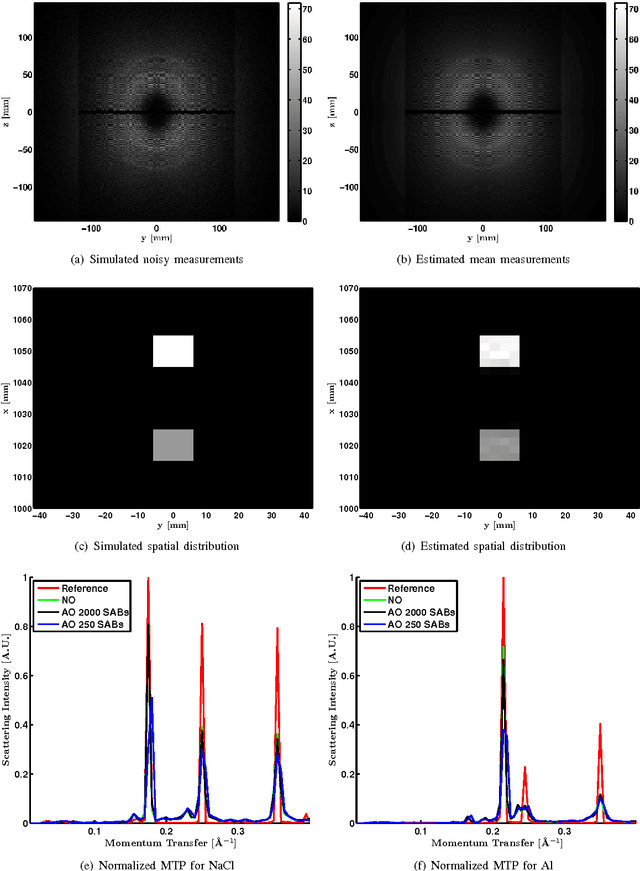
In x-ray coherent scatter tomography, tomographic measurements of the forward scatter distribution are used to infer scatter densities within a volume. A radiopaque 2D pattern placed between the object and the detector array enables the disambiguation between different scatter events. The use of a fan beam source illumination to speed up data acquisition relative to a pencil beam presents computational challenges. To facilitate the use of iterative algorithms based on a penalized Poisson log-likelihood function, efficient computational implementation of the forward and backward models are needed. Our proposed implementation exploits physical symmetries and structural properties of the system and suggests a joint system-algorithm design, where the system design choices are influenced by computational considerations, and in turn lead to reduced reconstruction time. Computational-time speedups of approximately 146 and 32 are achieved in the computation of the forward and backward models, respectively. Results validating the forward model and reconstruction algorithm are presented on simulated analytic and Monte Carlo data.

Alternating Minimization Algorithm with Automatic Relevance Determination for Transmission Tomography under Poisson Noise

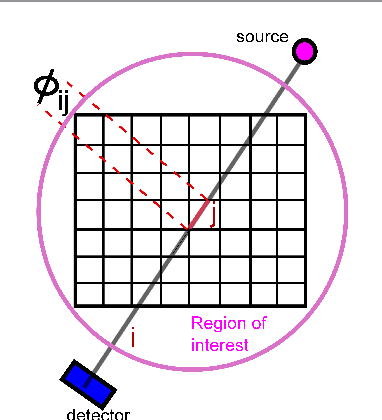
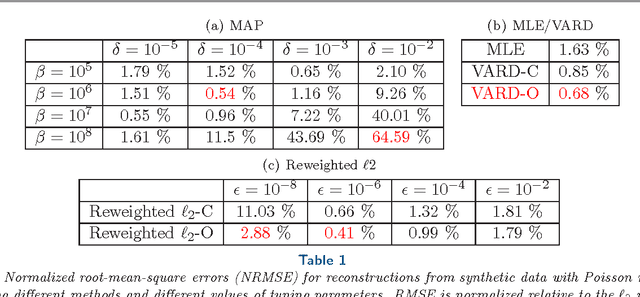
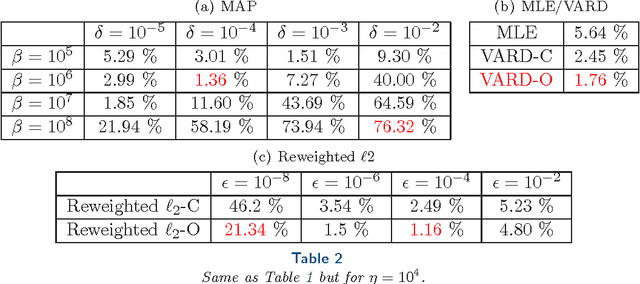
We propose a globally convergent alternating minimization (AM) algorithm for image reconstruction in transmission tomography, which extends automatic relevance determination (ARD) to Poisson noise models with Beer's law. The algorithm promotes solutions that are sparse in the pixel/voxel-differences domain by introducing additional latent variables, one for each pixel/voxel, and then learning these variables from the data using a hierarchical Bayesian model. Importantly, the proposed AM algorithm is free of any tuning parameters with image quality comparable to standard penalized likelihood methods. Our algorithm exploits optimization transfer principles which reduce the problem into parallel 1D optimization tasks (one for each pixel/voxel), making the algorithm feasible for large-scale problems. This approach considerably reduces the computational bottleneck of ARD associated with the posterior variances. Positivity constraints inherent in transmission tomography problems are also enforced. We demonstrate the performance of the proposed algorithm for x-ray computed tomography using synthetic and real-world datasets. The algorithm is shown to have much better performance than prior ARD algorithms based on approximate Gaussian noise models, even for high photon flux.

Multiresolution Approach to Acceleration of Iterative Image Reconstruction for X-Ray Imaging for Security Applications

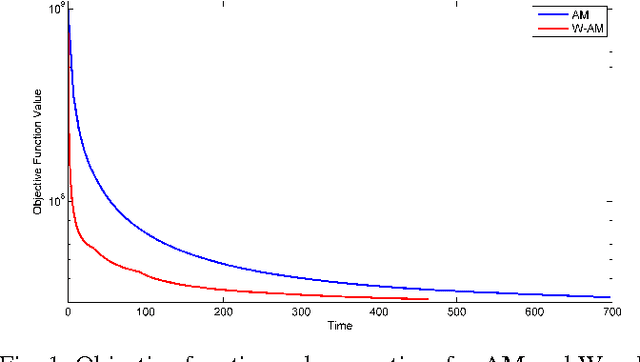
Three-dimensional x-ray CT image reconstruction in baggage scanning in security applications is an important research field. The variety of materials to be reconstructed is broader than medical x-ray imaging. Presence of high attenuating materials such as metal may cause artifacts if analytical reconstruction methods are used. Statistical modeling and the resultant iterative algorithms are known to reduce these artifacts and present good quantitative accuracy in estimates of linear attenuation coefficients. However, iterative algorithms may require computations in order to achieve quantitatively accurate results. For the case of baggage scanning, in order to provide fast accurate inspection throughput, they must be accelerated drastically. There are many approaches proposed in the literature to increase speed of convergence. This paper presents a new method that estimates the wavelet coefficients of the images in the discrete wavelet transform domain instead of the image space itself. Initially, surrogate functions are created around approximation coefficients only. As the iterations proceed, the wavelet tree on which the updates are made is expanded based on a criterion and detail coefficients at each level are updated and the tree is expanded this way. For example, in the smooth regions of the image the detail coefficients are not updated while the coefficients that represent the high-frequency component around edges are being updated, thus saving time by focusing computations where they are needed. This approach is implemented on real data from a SureScan (TM) x1000 Explosive Detection System and compared to straightforward implementation of the unregularized alternating minimization of O'Sullivan and Benac [1].