Jingwei Lu
Laplacian Prior Variational Automatic Relevance Determination for Transmission Tomography
Oct 26, 2017

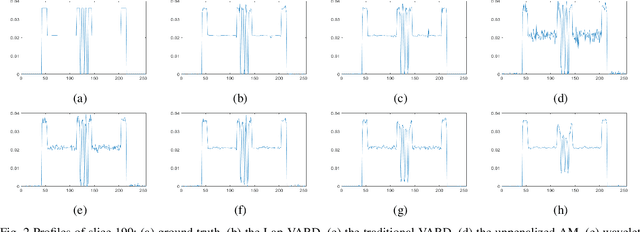
Abstract:In the classic sparsity-driven problems, the fundamental L-1 penalty method has been shown to have good performance in reconstructing signals for a wide range of problems. However this performance relies on a good choice of penalty weight which is often found from empirical experiments. We propose an algorithm called the Laplacian variational automatic relevance determination (Lap-VARD) that takes this penalty weight as a parameter of a prior Laplace distribution. Optimization of this parameter using an automatic relevance determination framework results in a balance between the sparsity and accuracy of signal reconstruction. Our algorithm is implemented in a transmission tomography model with sparsity constraint in wavelet domain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge