Spectrally Grouped Total Variation Reconstruction for Scatter Imaging Using ADMM

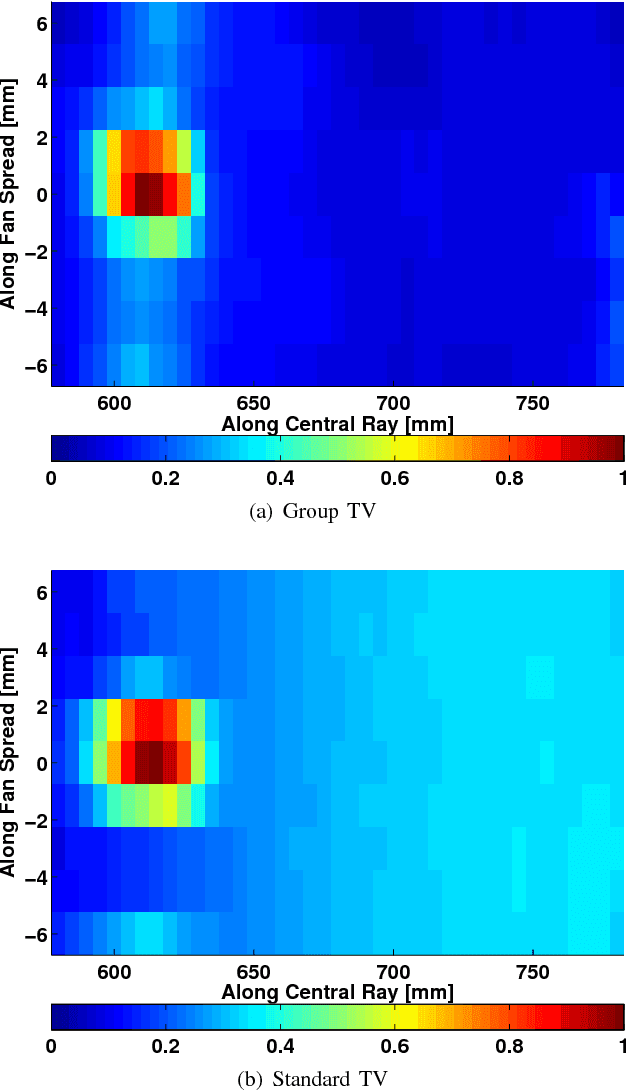
We consider X-ray coherent scatter imaging, where the goal is to reconstruct momentum transfer profiles (spectral distributions) at each spatial location from multiplexed measurements of scatter. Each material is characterized by a unique momentum transfer profile (MTP) which can be used to discriminate between different materials. We propose an iterative image reconstruction algorithm based on a Poisson noise model that can account for photon-limited measurements as well as various second order statistics of the data. To improve image quality, previous approaches use edge-preserving regularizers to promote piecewise constancy of the image in the spatial domain while treating each spectral bin separately. Instead, we propose spectrally grouped regularization that promotes piecewise constant images along the spatial directions but also ensures that the MTPs of neighboring spatial bins are similar, if they contain the same material. We demonstrate that this group regularization results in improvement of both spectral and spatial image quality. We pursue an optimization transfer approach where convex decompositions are used to lift the problem such that all hyper-voxels can be updated in parallel and in closed-form. The group penalty introduces a challenge since it is not directly amendable to these decompositions. We use the alternating directions method of multipliers (ADMM) to replace the original problem with an equivalent sequence of sub-problems that are amendable to convex decompositions, leading to a highly parallel algorithm. We demonstrate the performance on real data.

Joint System and Algorithm Design for Computationally Efficient Fan Beam Coded Aperture X-ray Coherent Scatter Imaging

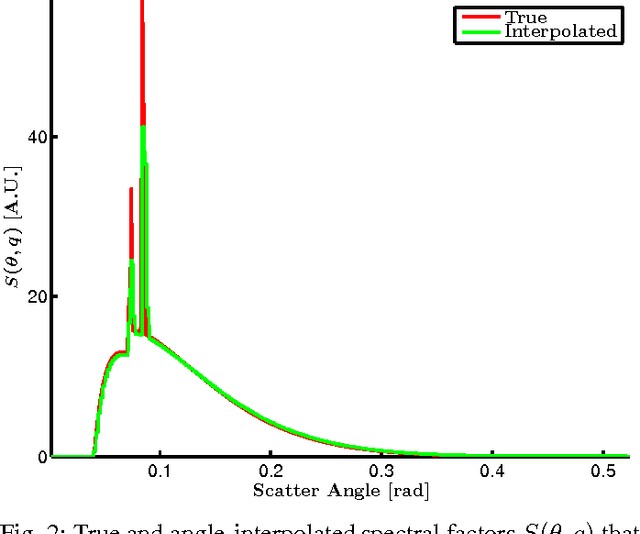
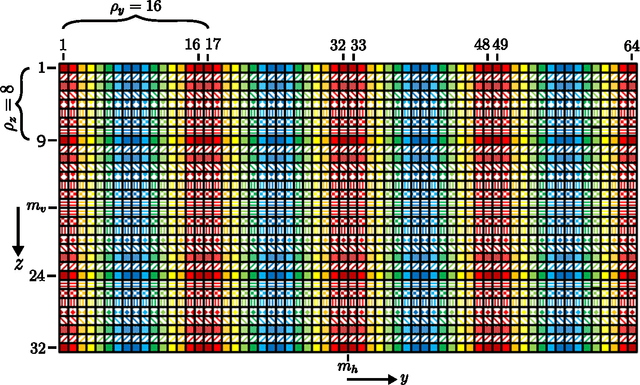
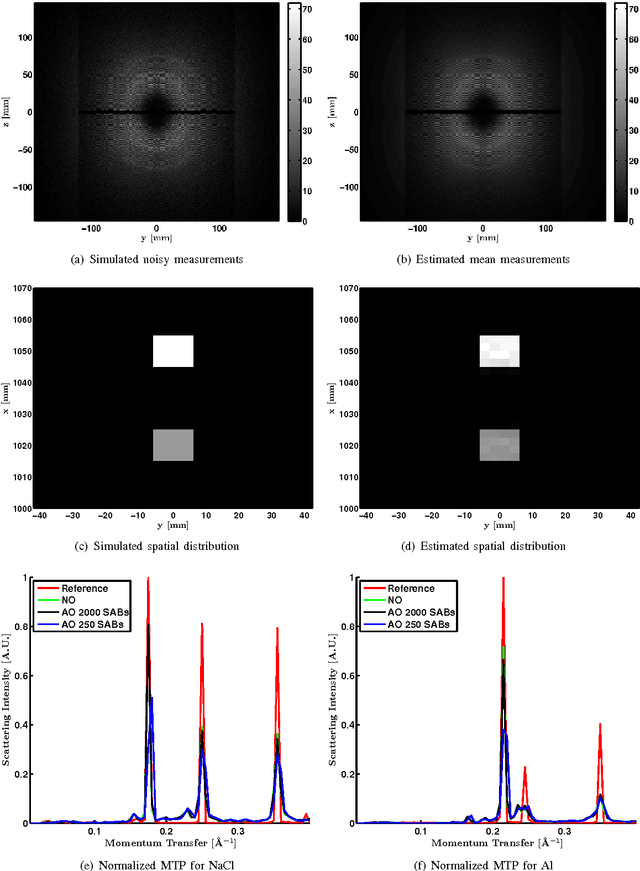
In x-ray coherent scatter tomography, tomographic measurements of the forward scatter distribution are used to infer scatter densities within a volume. A radiopaque 2D pattern placed between the object and the detector array enables the disambiguation between different scatter events. The use of a fan beam source illumination to speed up data acquisition relative to a pencil beam presents computational challenges. To facilitate the use of iterative algorithms based on a penalized Poisson log-likelihood function, efficient computational implementation of the forward and backward models are needed. Our proposed implementation exploits physical symmetries and structural properties of the system and suggests a joint system-algorithm design, where the system design choices are influenced by computational considerations, and in turn lead to reduced reconstruction time. Computational-time speedups of approximately 146 and 32 are achieved in the computation of the forward and backward models, respectively. Results validating the forward model and reconstruction algorithm are presented on simulated analytic and Monte Carlo data.