Benchmarking Offline Reinforcement Learning Algorithms for E-Commerce Order Fraud Evaluation

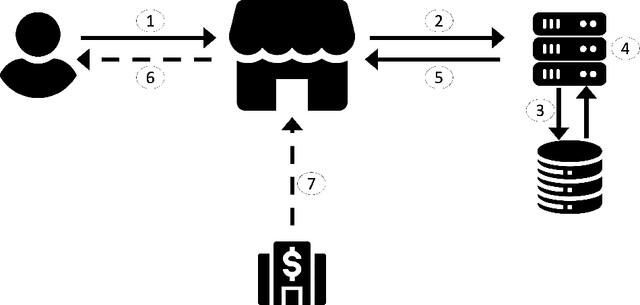
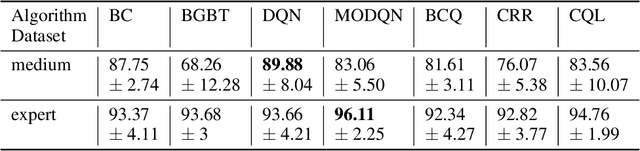
Amazon and other e-commerce sites must employ mechanisms to protect their millions of customers from fraud, such as unauthorized use of credit cards. One such mechanism is order fraud evaluation, where systems evaluate orders for fraud risk, and either "pass" the order, or take an action to mitigate high risk. Order fraud evaluation systems typically use binary classification models that distinguish fraudulent and legitimate orders, to assess risk and take action. We seek to devise a system that considers both financial losses of fraud and long-term customer satisfaction, which may be impaired when incorrect actions are applied to legitimate customers. We propose that taking actions to optimize long-term impact can be formulated as a Reinforcement Learning (RL) problem. Standard RL methods require online interaction with an environment to learn, but this is not desirable in high-stakes applications like order fraud evaluation. Offline RL algorithms learn from logged data collected from the environment, without the need for online interaction, making them suitable for our use case. We show that offline RL methods outperform traditional binary classification solutions in SimStore, a simplified e-commerce simulation that incorporates order fraud risk. We also propose a novel approach to training offline RL policies that adds a new loss term during training, to better align policy exploration with taking correct actions.

Alternating Minimization Algorithm with Automatic Relevance Determination for Transmission Tomography under Poisson Noise

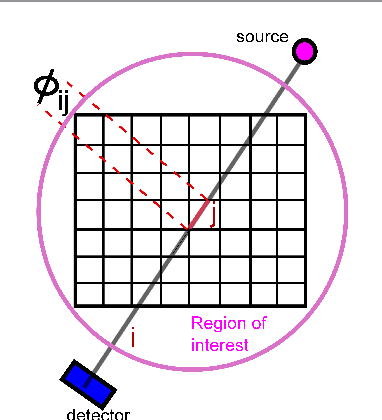
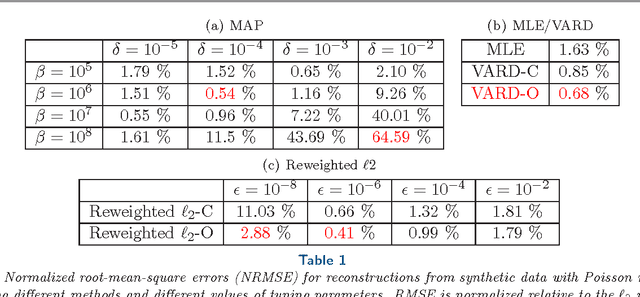
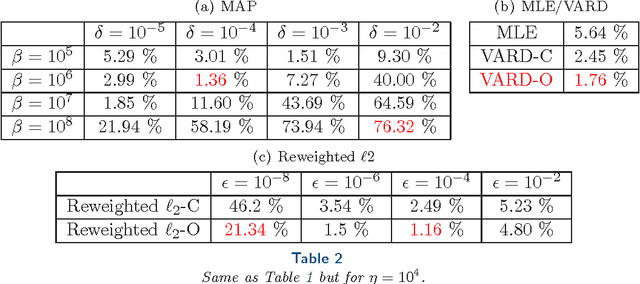
We propose a globally convergent alternating minimization (AM) algorithm for image reconstruction in transmission tomography, which extends automatic relevance determination (ARD) to Poisson noise models with Beer's law. The algorithm promotes solutions that are sparse in the pixel/voxel-differences domain by introducing additional latent variables, one for each pixel/voxel, and then learning these variables from the data using a hierarchical Bayesian model. Importantly, the proposed AM algorithm is free of any tuning parameters with image quality comparable to standard penalized likelihood methods. Our algorithm exploits optimization transfer principles which reduce the problem into parallel 1D optimization tasks (one for each pixel/voxel), making the algorithm feasible for large-scale problems. This approach considerably reduces the computational bottleneck of ARD associated with the posterior variances. Positivity constraints inherent in transmission tomography problems are also enforced. We demonstrate the performance of the proposed algorithm for x-ray computed tomography using synthetic and real-world datasets. The algorithm is shown to have much better performance than prior ARD algorithms based on approximate Gaussian noise models, even for high photon flux.