Relational Pooling for Graph Representations

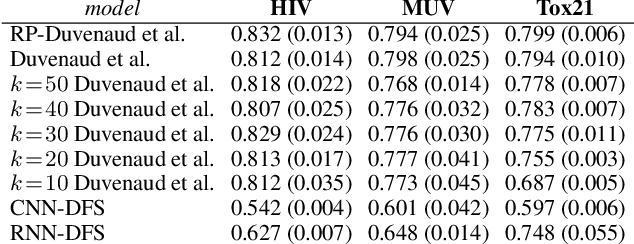
This work generalizes graph neural networks (GNNs) beyond those based on the Weisfeiler-Lehman (WL) algorithm, graph Laplacians, and graph diffusion kernels. Our approach, denoted Relational Pooling (RP), draws from the theory of finite partial exchangeability to provide a framework with maximal representation power for graphs. RP can work with existing graph representation models, and somewhat counterintuitively, can make them even more powerful than the original WL isomorphism test. Additionally, RP is the first theoretically sound framework to use architectures like Recurrent Neural Networks and Convolutional Neural Networks for graph classification. RP also has graph kernels as a special case. We demonstrate improved performance of novel RP-based graph representations over current state-of-the-art methods on a number of tasks.