Flexible Mixture Modeling on Constrained Spaces

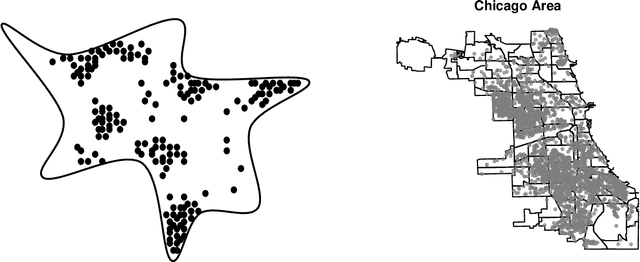
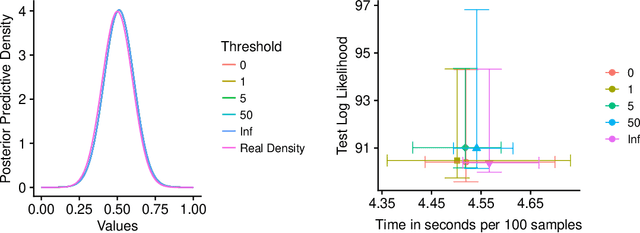
This paper addresses challenges in flexibly modeling multimodal data that lie on constrained spaces. Applications include climate or crime measurements in a geographical area, or flow-cytometry experiments, where unsuitable recordings are discarded. A simple approach to modeling such data is through the use of mixture models, with each component following an appropriate truncated distribution. Problems arise when the truncation involves complicated constraints, leading to difficulties in specifying the component distributions, and in evaluating their normalization constants. Bayesian inference over the parameters of these models results in posterior distributions that are doubly-intractable. We address this problem via an algorithm based on rejection sampling and data augmentation. We view samples from a truncated distribution as outcomes of a rejection sampling scheme, where proposals are made from a simple mixture model, and are rejected if they violate the constraints. Our scheme proceeds by imputing the rejected samples given mixture parameters, and then resampling parameters given all samples. We study two modeling approaches: mixtures of truncated components and truncated mixtures of components. In both situations, we describe exact Markov chain Monte Carlo sampling algorithms, as well as approximations that bound the number of rejected samples, achieving computational efficiency and lower variance at the cost of asymptotic bias. Overall, our methodology only requires practitioners to provide an indicator function for the set of interest. We present results on simulated data and apply our algorithm to two problems, one involving flow-cytometry data, and the other, crime recorded in the city of Chicago.