Generalized Regret Analysis of Thompson Sampling using Fractional Posteriors

Thompson sampling (TS) is one of the most popular and earliest algorithms to solve stochastic multi-armed bandit problems. We consider a variant of TS, named $\alpha$-TS, where we use a fractional or $\alpha$-posterior ($\alpha\in(0,1)$) instead of the standard posterior distribution. To compute an $\alpha$-posterior, the likelihood in the definition of the standard posterior is tempered with a factor $\alpha$. For $\alpha$-TS we obtain both instance-dependent $\mathcal{O}\left(\sum_{k \neq i^*} \Delta_k\left(\frac{\log(T)}{C(\alpha)\Delta_k^2} + \frac{1}{2} \right)\right)$ and instance-independent $\mathcal{O}(\sqrt{KT\log K})$ frequentist regret bounds under very mild conditions on the prior and reward distributions, where $\Delta_k$ is the gap between the true mean rewards of the $k^{th}$ and the best arms, and $C(\alpha)$ is a known constant. Both the sub-Gaussian and exponential family models satisfy our general conditions on the reward distribution. Our conditions on the prior distribution just require its density to be positive, continuous, and bounded. We also establish another instance-dependent regret upper bound that matches (up to constants) to that of improved UCB [Auer and Ortner, 2010]. Our regret analysis carefully combines recent theoretical developments in the non-asymptotic concentration analysis and Bernstein-von Mises type results for the $\alpha$-posterior distribution. Moreover, our analysis does not require additional structural properties such as closed-form posteriors or conjugate priors.

An Active Learning-based Approach for Hosting Capacity Analysis in Distribution Systems

With the increasing amount of distributed energy resources (DERs) integration, there is a significant need to model and analyze hosting capacity (HC) for future electric distribution grids. Hosting capacity analysis (HCA) examines the amount of DERs that can be safely integrated into the grid and is a challenging task in full generality because there are many possible integration of DERs in foresight. That is, there are numerous extreme points between feasible and infeasible sets. Moreover, HC depends on multiple factors such as (a) adoption patterns of DERs that depend on socio-economic behaviors and (b) how DERs are controlled and managed. These two factors are intrinsic to the problem space because not all integration of DERs may be centrally planned, and could largely change our understanding about HC. This paper addresses the research gap by capturing the two factors (a) and (b) in HCA and by identifying a few most insightful HC scenarios at the cost of domain knowledge. We propose a data-driven HCA framework and introduce active learning in HCA to effectively explore scenarios. Active learning in HCA and characteristics of HC with respect to the two factors (a) and (b) are illustrated in a 3-bus example. Next, detailed large-scale studies are proposed to understand the significance of (a) and (b). Our findings suggest that HC and its interpretations significantly change subject to the two factors (a) and (b).

Graphical Dirichlet Process

We consider the problem of clustering grouped data with possibly non-exchangeable groups whose dependencies can be characterized by a directed acyclic graph. To allow the sharing of clusters among the non-exchangeable groups, we propose a Bayesian nonparametric approach, termed graphical Dirichlet process, that jointly models the dependent group-specific random measures by assuming each random measure to be distributed as a Dirichlet process whose concentration parameter and based probability measure depend on those of its parent groups. The resulting joint stochastic process respects the Markov property of the directed acyclic graph that links the groups. We characterize the graphical Dirichlet process using a novel hypergraph representation as well as the stick-breaking representation, the restaurant-type representation, and the representation as a limit of a finite mixture model. We develop an efficient posterior inference algorithm and illustrate our model with simulations and a real grouped single-cell data.

Balance is Essence: Accelerating Sparse Training via Adaptive Gradient Correction

Despite impressive performance on a wide variety of tasks, deep neural networks require significant memory and computation costs, prohibiting their application in resource-constrained scenarios. Sparse training is one of the most common techniques to reduce these costs, however, the sparsity constraints add difficulty to the optimization, resulting in an increase in training time and instability. In this work, we aim to overcome this problem and achieve space-time co-efficiency. To accelerate and stabilize the convergence of sparse training, we analyze the gradient changes and develop an adaptive gradient correction method. Specifically, we approximate the correlation between the current and previous gradients, which is used to balance the two gradients to obtain a corrected gradient. Our method can be used with most popular sparse training pipelines under both standard and adversarial setups. Theoretically, we prove that our method can accelerate the convergence rate of sparse training. Extensive experiments on multiple datasets, model architectures, and sparsities demonstrate that our method outperforms leading sparse training methods by up to \textbf{5.0\%} in accuracy given the same number of training epochs, and reduces the number of training epochs by up to \textbf{52.1\%} to achieve the same accuracy.

Factorized Fusion Shrinkage for Dynamic Relational Data

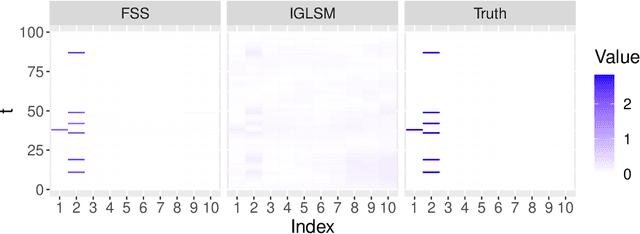
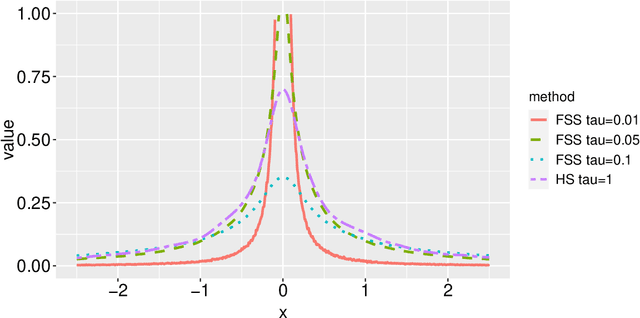
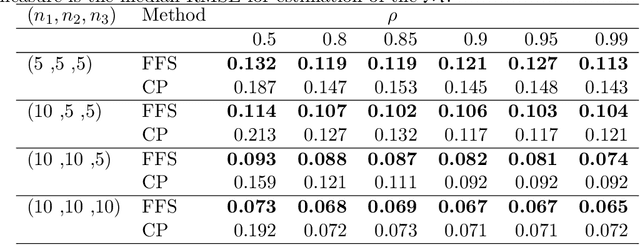
Modern data science applications often involve complex relational data with dynamic structures. An abrupt change in such dynamic relational data is typically observed in systems that undergo regime changes due to interventions. In such a case, we consider a factorized fusion shrinkage model in which all decomposed factors are dynamically shrunk towards group-wise fusion structures, where the shrinkage is obtained by applying global-local shrinkage priors to the successive differences of the row vectors of the factorized matrices. The proposed priors enjoy many favorable properties in comparison and clustering of the estimated dynamic latent factors. Comparing estimated latent factors involves both adjacent and long-term comparisons, with the time range of comparison considered as a variable. Under certain conditions, we demonstrate that the posterior distribution attains the minimax optimal rate up to logarithmic factors. In terms of computation, we present a structured mean-field variational inference framework that balances optimal posterior inference with computational scalability, exploiting both the dependence among components and across time. The framework can accommodate a wide variety of models, including dynamic matrix factorization, latent space models for networks and low-rank tensors. The effectiveness of our methodology is demonstrated through extensive simulations and real-world data analysis.

Structured Optimal Variational Inference for Dynamic Latent Space Models

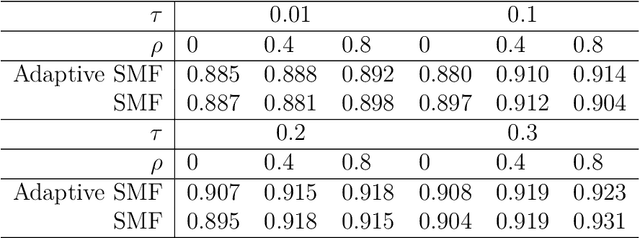
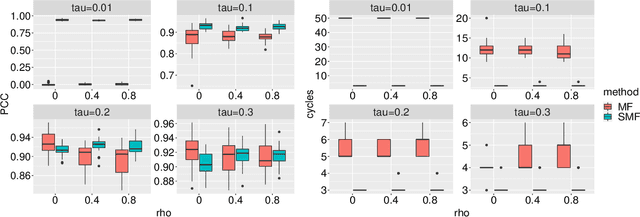
We consider a latent space model for dynamic networks, where our objective is to estimate the pairwise inner products of the latent positions. To balance posterior inference and computational scalability, we present a structured mean-field variational inference framework, where the time-dependent properties of the dynamic networks are exploited to facilitate computation and inference. Additionally, an easy-to-implement block coordinate ascent algorithm is developed with message-passing type updates in each block, whereas the complexity per iteration is linear with the number of nodes and time points. To facilitate learning of the pairwise latent distances, we adopt a Gamma prior for the transition variance different from the literature. To certify the optimality, we demonstrate that the variational risk of the proposed variational inference approach attains the minimax optimal rate under certain conditions. En route, we derive the minimax lower bound, which might be of independent interest. To best of our knowledge, this is the first such exercise for dynamic latent space models. Simulations and real data analysis demonstrate the efficacy of our methodology and the efficiency of our algorithm. Finally, our proposed methodology can be readily extended to the case where the scales of the latent nodes are learned in a nodewise manner.

Continuous shrinkage prior revisited: a collapsing behavior and remedy

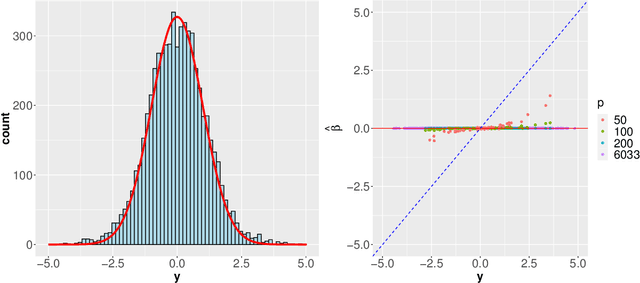
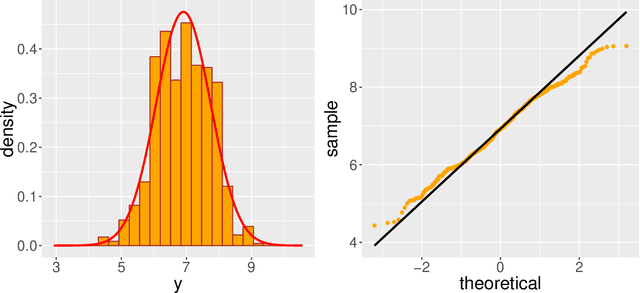
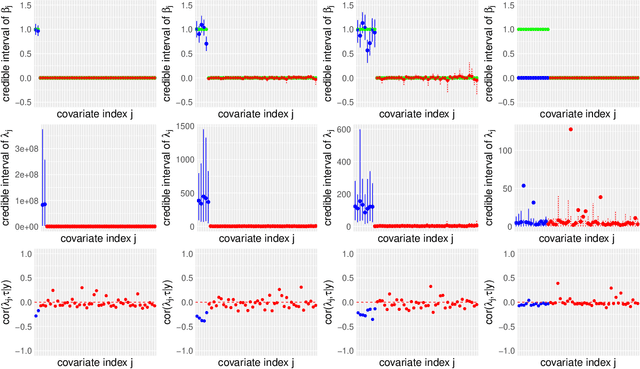
Modern genomic studies are increasingly focused on identifying more and more genes clinically associated with a health response. Commonly used Bayesian shrinkage priors are designed primarily to detect only a handful of signals when the dimension of the predictors is very high. In this article, we investigate the performance of a popular continuous shrinkage prior in the presence of relatively large number of true signals. We draw attention to an undesirable phenomenon; the posterior mean is rendered very close to a null vector, caused by a sharp underestimation of the global-scale parameter. The phenomenon is triggered by the absence of a tail-index controlling mechanism in the Bayesian shrinkage priors. We provide a remedy by developing a global-local-tail shrinkage prior which can automatically learn the tail-index and can provide accurate inference even in the presence of moderately large number of signals. The collapsing behavior of the Horseshoe with its remedy is exemplified in numerical examples and in two gene expression datasets.

Directionally Dependent Multi-View Clustering Using Copula Model

In recent biomedical scientific problems, it is a fundamental issue to integratively cluster a set of objects from multiple sources of datasets. Such problems are mostly encountered in genomics, where data is collected from various sources, and typically represent distinct yet complementary information. Integrating these data sources for multi-source clustering is challenging due to their complex dependence structure including directional dependency. Particularly in genomics studies, it is known that there is certain directional dependence between DNA expression, DNA methylation, and RNA expression, widely called The Central Dogma. Most of the existing multi-view clustering methods either assume an independent structure or pair-wise (non-directional) dependency, thereby ignoring the directional relationship. Motivated by this, we propose a copula-based multi-view clustering model where a copula enables the model to accommodate the directional dependence existing in the datasets. We conduct a simulation experiment where the simulated datasets exhibiting inherent directional dependence: it turns out that ignoring the directional dependence negatively affects the clustering performance. As a real application, we applied our model to the breast cancer tumor samples collected from The Cancer Genome Altas (TCGA).